Bray-curtis-unähnlichkeit: definition und beispiele

Die nach J. Roger Bray und John Thomas Curtis benannte Bray-Curtis-Unähnlichkeit ist eine Möglichkeit, die Unähnlichkeit zwischen zwei verschiedenen Standorten zu messen.

In der Ökologie und Biologie wird es häufig verwendet, um den Unterschied zwischen zwei Standorten hinsichtlich der dort vorkommenden Arten zu quantifizieren.

Die Bray-Curtis-Unähnlichkeit wird wie folgt berechnet:

BC _ij = 1 – (2*C _ij ) / (S _i + S _j )

Gold:

• C _ij : Die Summe der niedrigsten Werte für die an jedem Standort gefundenen Arten.
• S _i : Die Gesamtzahl der am Standort i gezählten Exemplare
• S _j : Die Gesamtzahl der am Standort j gezählten Exemplare

Die Bray-Curtis-Unähnlichkeit liegt immer zwischen 0 und 1, wobei:

• 0 gibt an, dass zwei Standorte keine Unähnlichkeit aufweisen. Mit anderen Worten: Sie haben von jeder Artenart genau die gleiche Anzahl.
• 1 zeigt an, dass zwei Standorte völlig unterschiedlich sind. Mit anderen Worten, es gibt keine gemeinsame Art derselben Art.

Das folgende Beispiel zeigt, wie die Bray-Curtis-Unähnlichkeit für zwei Standorte berechnet wird.

Beispiel: Berechnung der Bray-Curtis-Unähnlichkeit

Angenommen, ein Botaniker geht los und zählt die Anzahl von fünf verschiedenen Pflanzenarten (A, B, C, D und E) an zwei verschiedenen Standorten.

Die folgende Tabelle fasst die von ihr gesammelten Daten zusammen:

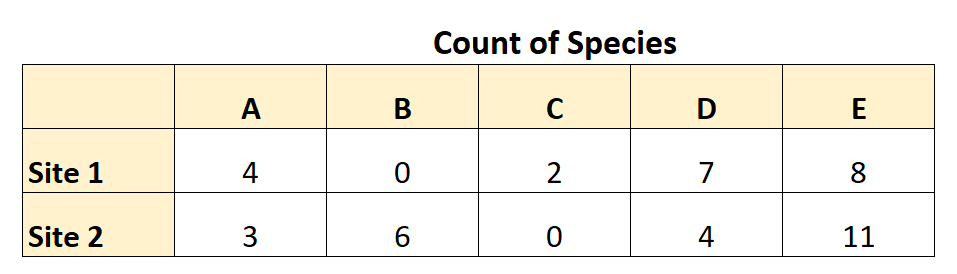
Anhand dieser Daten kann sie die Bray-Curtis-Unähnlichkeit wie folgt berechnen:

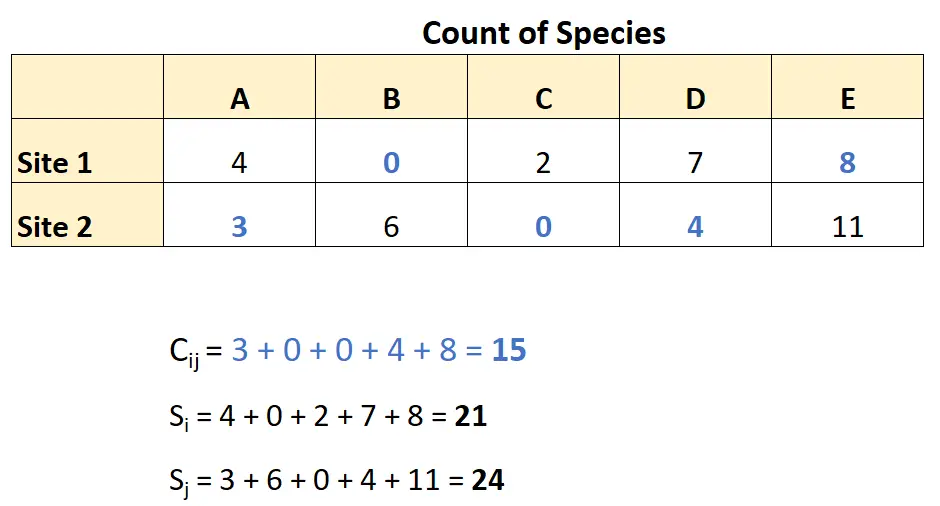
Durch Integration dieser Zahlen in die Bray-Curtis-Unähnlichkeitsformel erhalten wir:

• BC _ij = 1 – (2*C _ij ) / (S _i + S _j )
• BC _ij = 1 – (2*15) / (21 + 24)
• BC _ij = 0,33

Die Bray-Curtis-Unähnlichkeit zwischen diesen beiden Standorten beträgt 0,33 .

Schlüsselannahme der Bray-Curtis-Unähnlichkeit

Die Bray-Curtis-Unähnlichkeit geht davon aus, dass die beiden Standorte gleich groß sind.

Dies ist eine entscheidende Annahme, denn wenn ein Standort viermal größer ist als der andere, werden wir natürlicherweise mehr Arten auf dem größeren Standort haben als auf dem kleineren Standort, einfach weil dort viel mehr Fläche abgedeckt werden muss.

Um dies zu veranschaulichen, nehmen wir an, dass einer der Standorte, für den der Botaniker Daten gesammelt hat, viermal größer ist als der andere Standort:

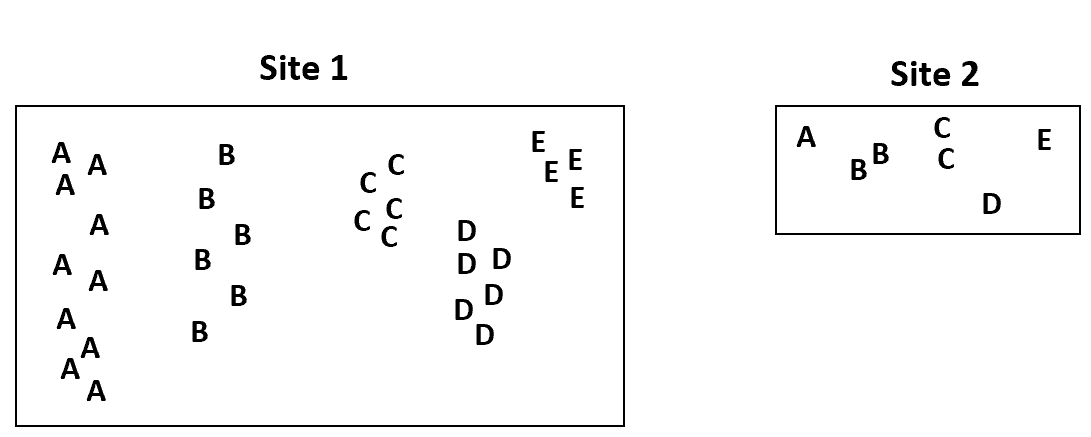
Wir würden eine viel höhere Häufigkeit der Arten an Standort 1 erwarten, einfach weil dieser viel größer ist als Standort 2.

Wenn wir also die Bray-Curtis-Unähnlichkeit berechnen, wäre sie ziemlich groß. Dies wäre jedoch irreführend, da der Unterschied zwischen den beiden Standorten nicht in ihrer Zusammensetzung, sondern vielmehr in ihrer Größe liegt.