So führen sie einen breusch-pagan-test in stata durch

Die multiple lineare Regression ist eine Methode, mit der wir die Beziehung zwischen mehreren erklärenden Variablen und einer Antwortvariablen verstehen können.

Leider tritt bei der Regression häufig ein Problem auf, das sogenannte Heteroskedastizität , bei dem es zu einer systematischen Änderung der Varianz der Residuen über einen Bereich gemessener Werte kommt.

Ein Test, mit dem wir feststellen können, ob Heteroskedastizität vorliegt, ist der Breusch-Pagan-Test . Dieser Test erzeugt eine Chi-Quadrat-Teststatistik und einen entsprechenden p-Wert.

Wenn der p-Wert unter einem bestimmten Schwellenwert liegt (übliche Werte sind 0,01, 0,05 und 0,10), gibt es genügend Beweise dafür, dass Heteroskedastizität vorliegt.

In diesem Tutorial wird erläutert, wie Sie einen Breusch-Pagan-Test in Stata durchführen.

Beispiel: Breusch-Pagan-Test in Stata

Wir werden den automatisch integrierten Stata-Datensatz verwenden, um zu veranschaulichen, wie der Breusch-Pagan-Test durchgeführt wird.

Schritt 1: Daten laden und anzeigen.

Verwenden Sie zunächst den folgenden Befehl, um die Daten zu laden:

automatische Nutzung des Systems

Anschließend lassen Sie sich die Rohdaten mit folgendem Befehl anzeigen:

br

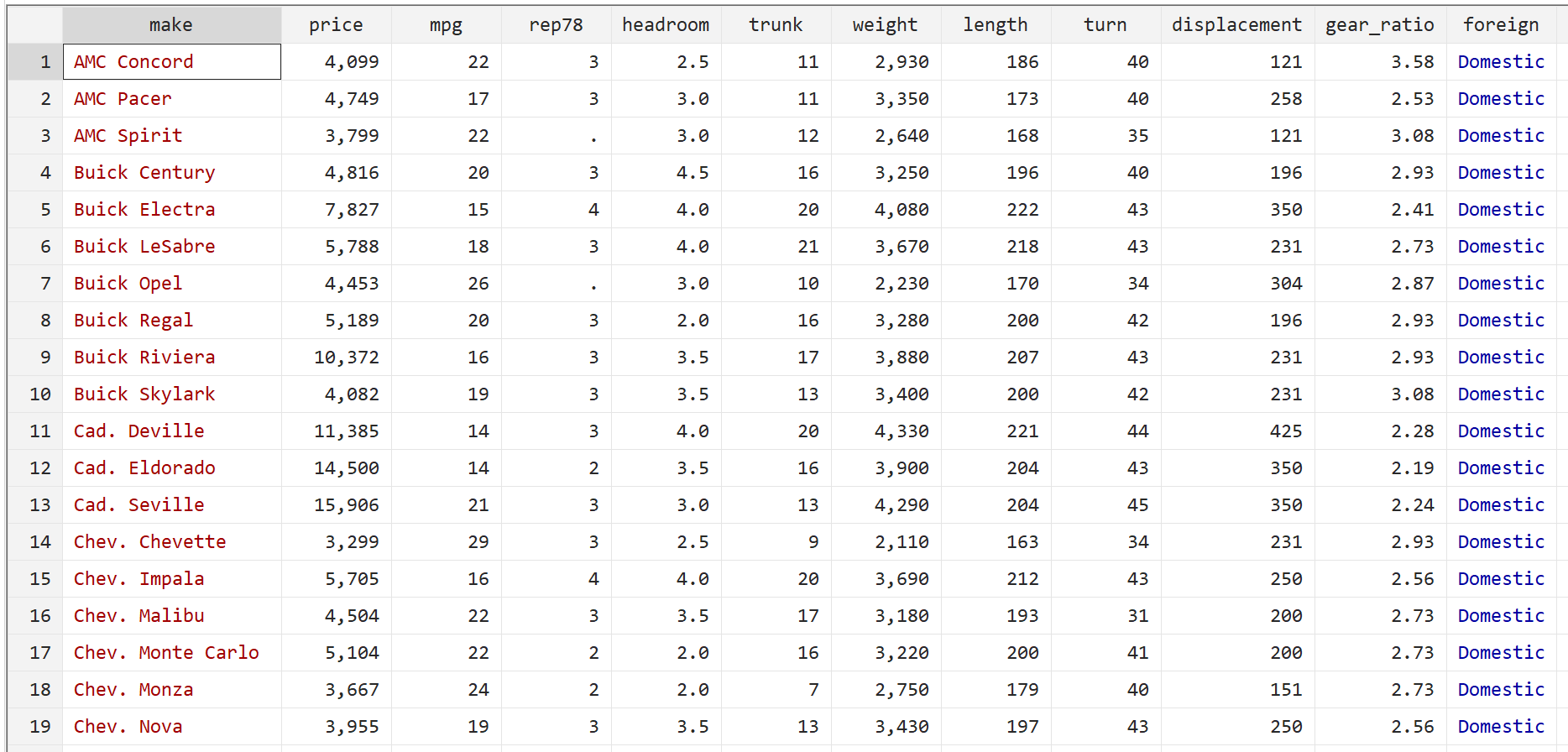
Schritt 2: Führen Sie eine multiple lineare Regression durch.

Als Nächstes geben wir den folgenden Befehl ein, um eine multiple lineare Regression durchzuführen, wobei der Preis als Antwortvariable und mpg und Gewicht als erklärende Variablen verwendet werden:

Regressionspreis mpg Gewicht

Schritt 3: Führen Sie den Breusch-Pagan-Test durch.

Sobald wir das Regressionsmodell angepasst haben, können wir den Breusch-Pagan-Test mit dem Befehl hettest durchführen, der für „Heteroskedastizitätstest“ steht:

das heißeste

So interpretieren Sie das Ergebnis:

Ho: Dies ist die Nullhypothese des Tests, die besagt, dass zwischen den Residuen eine konstante Varianz besteht.

Variablen: Hier erfahren wir, welche Antwortvariable im Regressionsmodell verwendet wurde. In diesem Fall war es der variable Preis .

chi2(1): Dies ist die Chi-Quadrat-Teststatistik des Tests. In diesem Fall ist es 14:78 Uhr.

Prob > chi2: Dies ist der p-Wert, der der Chi-Quadrat-Teststatistik entspricht. In diesem Fall ist es 0,0001. Da dieser Wert kleiner als 0,05 ist, können wir die Nullhypothese ablehnen und daraus schließen, dass in den Daten Heteroskedastizität vorliegt.

Was macht man als nächstes

Wenn Sie die Nullhypothese des Breusch-Pagan-Tests nicht ablehnen, liegt keine Heteroskedastizität vor und Sie können mit der Interpretation des Ergebnisses der ursprünglichen Regression fortfahren.

Wenn Sie jedoch die Nullhypothese des Breusch-Pagan-Tests ablehnen, bedeutet dies, dass in den Daten Heteroskedastizität vorliegt. In diesem Fall sind die in der Regressionsausgabetabelle angezeigten Standardfehler unzuverlässig. Es gibt mehrere Möglichkeiten, dieses Problem zu beheben, darunter:

1. Transformieren Sie die Antwortvariable. Sie können versuchen, eine Transformation für die Antwortvariable durchzuführen. Als Antwortvariable können Sie beispielsweise log(price) anstelle von price verwenden. Im Allgemeinen ist die Protokollierung der Antwortvariablen eine wirksame Möglichkeit, Heteroskedastizität zu beseitigen. Eine weitere übliche Transformation besteht darin, die Quadratwurzel der Antwortvariablen zu verwenden.

2. Verwenden Sie eine gewichtete Regression. Diese Art der Regression weist jedem Datenpunkt basierend auf der Varianz seines angepassten Werts eine Gewichtung zu. Im Wesentlichen werden dadurch Datenpunkte mit höheren Varianzen niedrig gewichtet, wodurch ihre Restquadrate reduziert werden. Durch die Verwendung geeigneter Gewichte kann das Problem der Heteroskedastizität beseitigt werden.

3. Verwenden Sie robuste Standardfehler. Robuste Standardfehler sind für das Problem der Heteroskedastizität „robuster“ und liefern tendenziell ein genaueres Maß für den wahren Standardfehler eines Regressionskoeffizienten. Sehen Sie sichdieses Tutorial an, um zu erfahren, wie Sie robuste Standardfehler bei der Regression in Stata verwenden.