Brown-forsythe-test in r: schritt-für-schritt-beispiel

Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen ein signifikanter Unterschied besteht oder nicht.

Eine der Annahmen einer einfaktoriellen ANOVA besteht darin, dass die Varianzen der Grundgesamtheiten, aus denen die Stichproben gezogen werden, gleich sind.

Eine der gebräuchlichsten Methoden, dies zu testen, ist die Verwendung eines Brown-Forsythe-Tests , einem statistischen Test, der die folgenden Annahmen verwendet:

• H ₀ : Die Varianzen zwischen den Populationen sind gleich.
• H _A : Die Unterschiede zwischen den Populationen sind nicht gleich.

Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (z. B. α = 0,05), lehnen wir die Nullhypothese ab und kommen zu dem Schluss, dass die Varianzen zwischen verschiedenen Populationen nicht gleich sind.

Dieses Tutorial bietet ein schrittweises Beispiel für die Durchführung eines Brown-Forsythe-Tests in R.

Schritt 1: Geben Sie die Daten ein

Angenommen, wir möchten wissen, ob drei verschiedene Trainingsprogramme zu unterschiedlichem Gewichtsverlust führen.

Um dies zu testen, rekrutieren wir 90 Personen und weisen 30 nach dem Zufallsprinzip die Nutzung jedes Programms zu. Anschließend messen wir den Gewichtsverlust jeder Person nach einem Monat.

Der folgende Datensatz enthält Informationen über die mit jedem Programm verlorene Gewichtsmenge:

 #make this example reproducible
set.seed(0)

#create data frame
data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)),
                   weight_loss = c( runif (30, 0, 3),
                                   runif (30, 0, 5),
                                   runif (30, 1, 7)))

#view first six rows of data frame
head(data)

# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458

Schritt 2: Fassen Sie die Daten zusammen und visualisieren Sie sie

Bevor wir einen Brown-Forsythe-Test durchführen, können wir Boxplots erstellen, um die Varianz des Gewichtsverlusts für jede Gruppe zu visualisieren:

 boxplot(weight_loss ~ program, data = data)

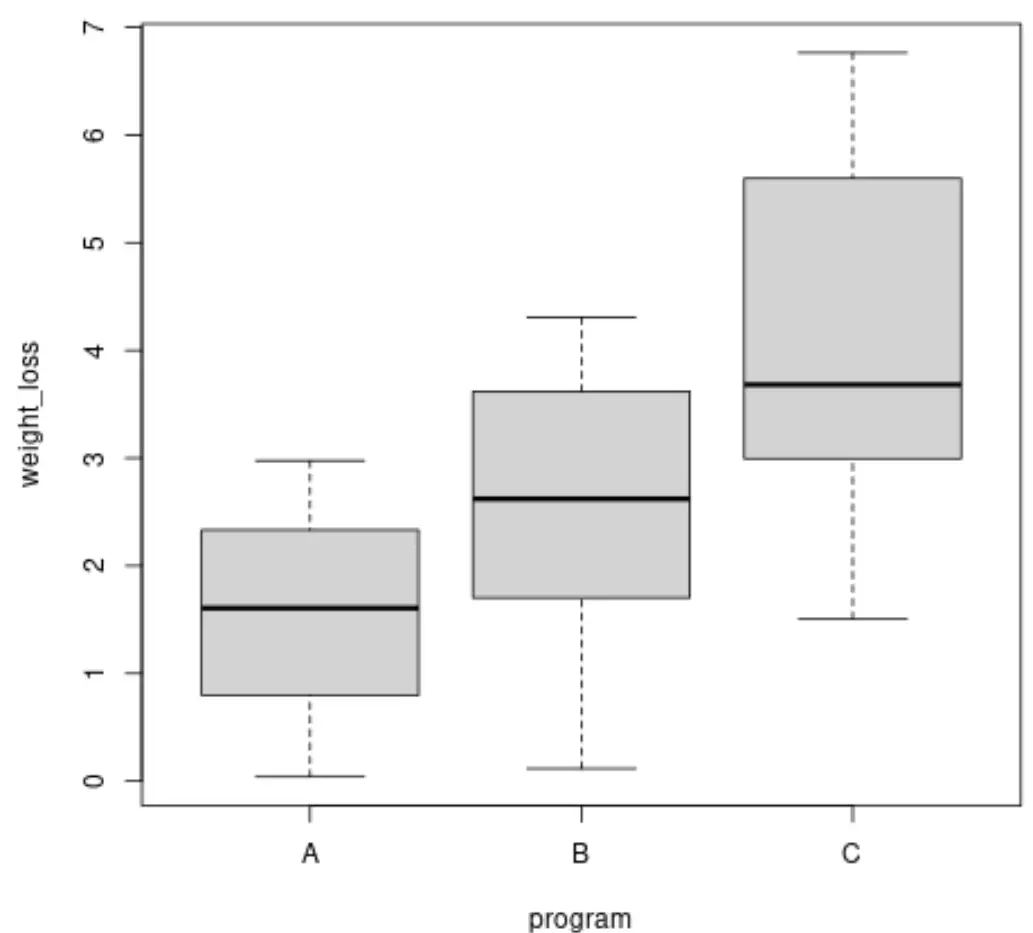
Wir können auch die Varianz des Gewichtsverlusts in jeder Gruppe berechnen:

 #load dplyr package
library (dplyr)

#calculate variance of weight loss by group
data %>%
group_by (program) %>%
  summarize (var=var(weight_loss))

# A tibble: 3 x 2
  program var
     
1 A 0.819
2 B 1.53 
3 C 2.46

Wir können sehen, dass die Varianzen zwischen den Gruppen unterschiedlich sind, aber um festzustellen, ob diese Unterschiede statistisch signifikant sind, können wir den Brown-Forsythe-Test durchführen.

Schritt 3: Führen Sie den Brown-Forsythe-Test durch

Um einen Brown-Forsythe-Test in R durchzuführen, können wir die Funktion bf.test() aus dem Paket onewaytests verwenden:

 #load onewaytests package
library (onewaytests)

#perform Brown-Forsythe test
bf.test(weight_loss ~ program, data = data)

  Brown-Forsythe Test (alpha = 0.05) 
-------------------------------------------------- ----------- 
  data: weight_loss and program 

  statistic: 30.83304 
  num df: 2 
  name df: 74.0272 
  p.value: 1.816529e-10 

  Result: Difference is statistically significant. 
-------------------------------------------------- -----------

Der p-Wert des Tests liegt unter 0,000, und wie das Ergebnis zeigt, sind die Varianzunterschiede zwischen den drei Gruppen statistisch signifikant.

Nächste Schritte

Wenn Sie die Nullhypothese des Brown-Forsythe-Tests nicht ablehnen können, können Sie eine einfache ANOVA für die Daten durchführen.

Wenn Sie jedoch die Nullhypothese ablehnen, bedeutet dies, dass die Annahme der Varianzgleichheit verletzt ist. In diesem Fall haben Sie zwei Möglichkeiten:

1. Führen Sie trotzdem eine einfaktorielle ANOVA durch.

Es stellt sich heraus, dass eine einfaktorielle ANOVA tatsächlich robust gegenüber ungleichen Varianzen ist, solange die größte Varianz nicht größer als das Vierfache der kleinsten Varianz ist.

In Schritt 2 des obigen Beispiels haben wir festgestellt, dass die kleinste Varianz 0,819 und die größte Varianz 2,46 betrug. Das Verhältnis der größten zur kleinsten Varianz beträgt also 2,46 / 0,819 = 3,003 .

Da dieser Wert kleiner als 4 ist, könnten wir einfach die einfaktorielle ANOVA durchführen.

2. Führen Sie einen Kruskal-Wallis-Test durch

Wenn das Verhältnis der größten Varianz zur kleinsten Varianz größer als 4 ist, kann man sich stattdessen für die Durchführung eines Kruskal-Wallis-Tests entscheiden. Dies wird als nichtparametrisches Äquivalent der einfaktoriellen ANOVA angesehen.

Ein Schritt-für-Schritt-Beispiel für einen Kruskal-Wallis-Test in R finden Sie hier .