So verwenden sie normales cdf in r (mit beispielen)

Sie können die folgenden Methoden verwenden, um mit der normalen CDF (kumulative Verteilungsfunktion) in R zu arbeiten:

Methode 1: Berechnen Sie normale CDF-Wahrscheinlichkeiten

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

#calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

Methode 2: Zeichnen Sie den normalen CDF

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ")

Die folgenden Beispiele zeigen, wie diese Methoden in der Praxis eingesetzt werden können.

Beispiel 1: Berechnen Sie normale CDF- Wahrscheinlichkeiten

Der folgende Code zeigt, wie die Wahrscheinlichkeit berechnet wird, dass eine Zufallsvariable in einer Standardnormalverteilung einen Wert kleiner als 1,96 annimmt:

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

[1] 0.9750021

Die Wahrscheinlichkeit, dass eine Zufallsvariable in einer Standardnormalverteilung einen Wert kleiner als 1,96 annimmt, beträgt 0,975 .

Mit dem Argument „lower.tail“ können wir auch die Wahrscheinlichkeit ermitteln, dass eine Zufallsvariable einen Wert größer als 1,96 annimmt:

 #calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

[1] 0.0249979

Und wir können die folgende Syntax verwenden, um die Wahrscheinlichkeit zu ermitteln, dass eine Zufallsvariable einen Wert zwischen zwei Werten in einer Standardnormalverteilung annimmt:

 #calculate probability that random value takes on value between -1.96 and 1.96
pnorm(1.96) - pnorm(-1.96)

[1] 0.9500042

Die Wahrscheinlichkeit, dass eine Zufallsvariable in einer Standardnormalverteilung einen Wert zwischen -1,96 und 1,96 annimmt, beträgt 0,95 .

Beispiel 2: Zeichnen des normalen CDF

Der folgende Code zeigt, wie man ein normales CDF plottet:

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ") 

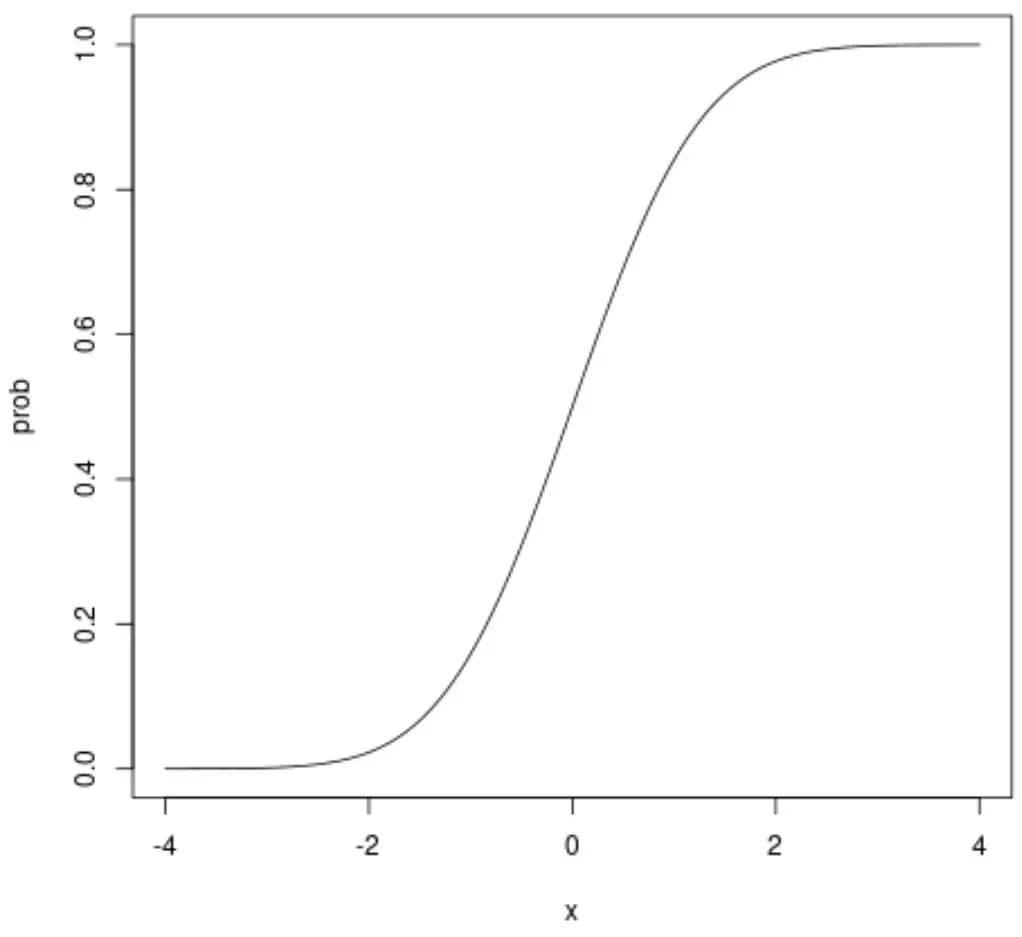
Die x-Achse zeigt die Werte einer Zufallsvariablen, die einer Standardnormalverteilung folgt, und die y-Achse zeigt die Wahrscheinlichkeit, dass eine Zufallsvariable einen Wert annimmt, der kleiner ist als der auf der x-Achse angezeigte Wert.

Wenn wir beispielsweise x = 1,96 betrachten, werden wir sehen, dass die kumulative Wahrscheinlichkeit, dass x kleiner als 1,96 ist, ungefähr 0,975 beträgt:

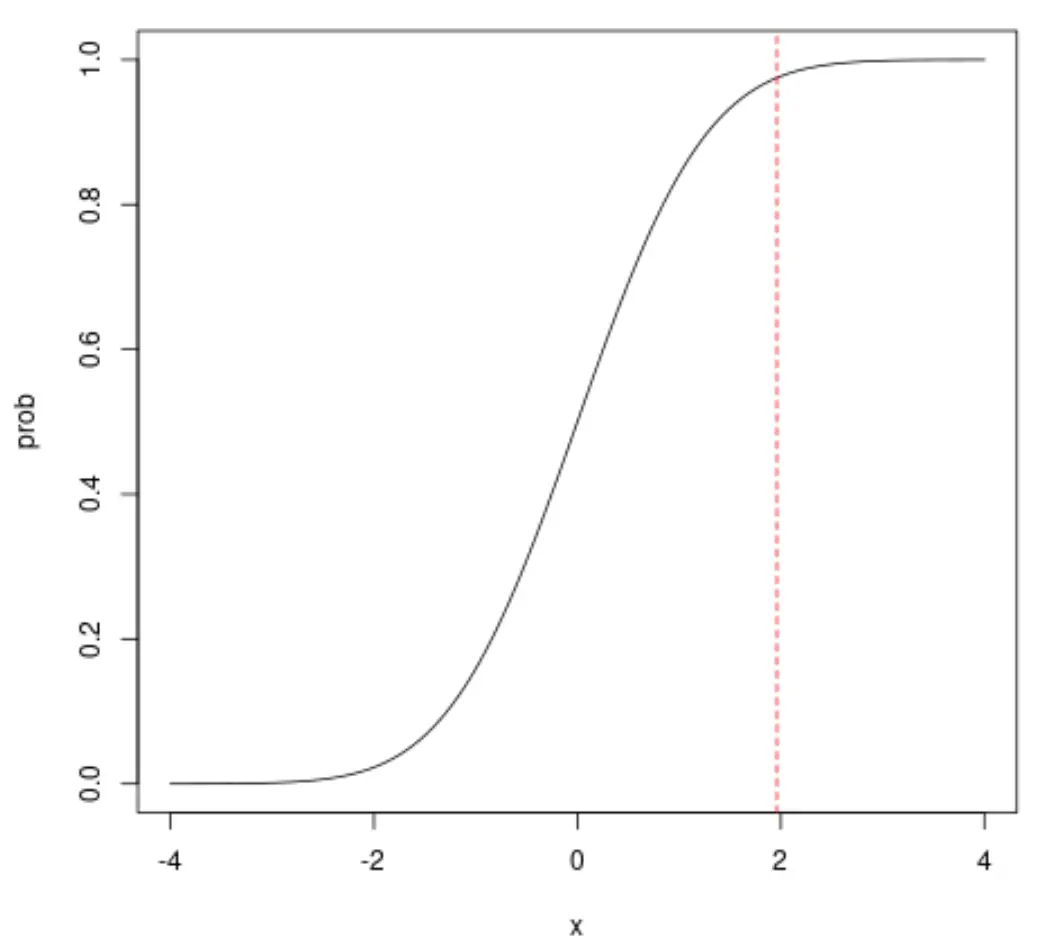
Beachten Sie, dass Sie auch die Ästhetik des normalen CDF-Plots ändern können:

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=' l ', col=' blue ', lwd= 2 , main=' Normal CDF ', ylab=' Cumulative Prob ') 

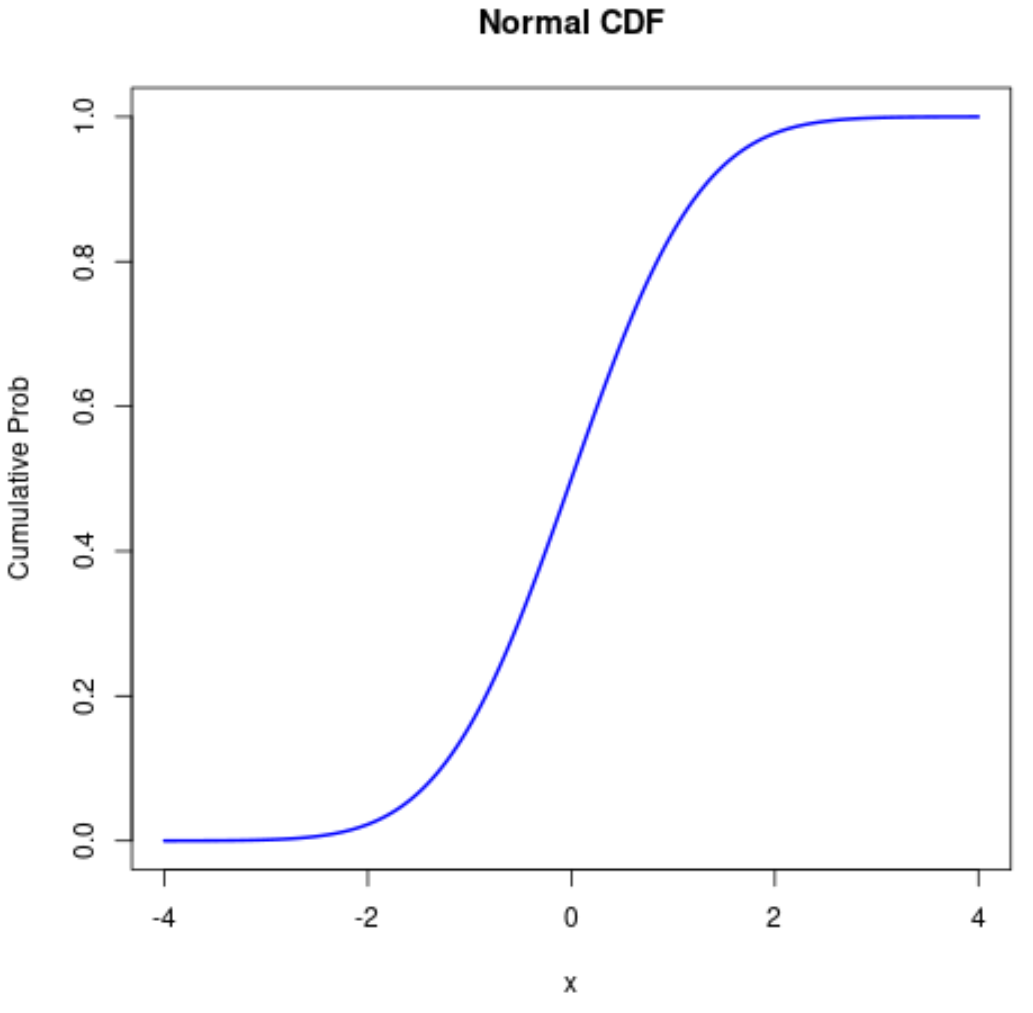
Verwandt: So verwenden Sie die seq-Funktion in R

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie andere gängige Vorgänge in R ausgeführt werden:

So zeichnen Sie eine Normalverteilung in R auf
So berechnen Sie Z-Scores in R
Eine Anleitung zu dnorm, pnorm, qnorm und rnorm in R