Chi-quadrat-anpassungstest auf einem ti-84-rechner

Mithilfe eines Chi-Quadrat-Anpassungstests wird ermittelt, ob eine kategoriale Variable einer hypothetischen Verteilung folgt oder nicht.

In diesem Tutorial wird erläutert, wie Sie einen Chi-Quadrat-Anpassungstest auf einem TI-84-Rechner durchführen.

Beispiel: Chi-Quadrat-Anpassungstest auf einem TI-84-Rechner

Ein Ladenbesitzer sagt, dass an jedem Tag der Woche gleich viele Kunden in sein Geschäft kommen. Um diese Hypothese zu testen, erfasst ein unabhängiger Forscher die Anzahl der Kunden, die in einer bestimmten Woche in den Laden kommen, und stellt Folgendes fest:

• Montag: 50 Kunden
• Dienstag: 60 Kunden
• Mittwoch: 40 Kunden
• Donnerstag: 47 Kunden
• Freitag: 53 Kunden

Mit den folgenden Schritten führen wir einen Chi-Quadrat-Anpassungstest durch, um festzustellen, ob die Daten mit der Behauptung des Ladenbesitzers übereinstimmen.

Schritt 1: Geben Sie die Daten ein.

Zunächst geben wir die Datenwerte für die erwartete Kundenzahl pro Tag und die beobachtete Kundenzahl pro Tag ein. Drücken Sie Stat und dann EDIT . Tragen Sie in Spalte L1 folgende Werte für die beobachtete Kundenzahl und in Spalte L2 die Werte für die erwartete Kundenzahl ein:

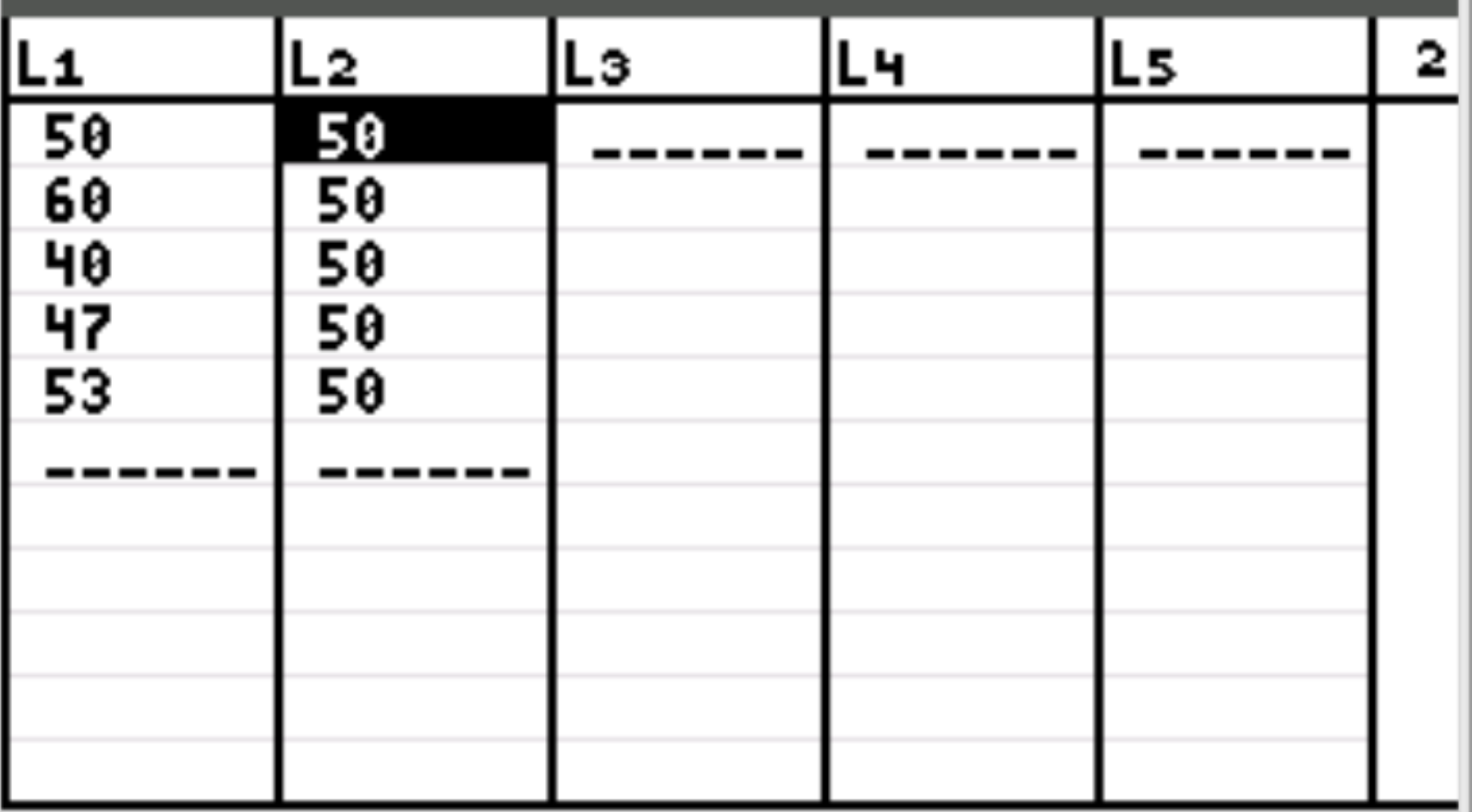
Hinweis: Insgesamt gab es 250 Kunden. Wenn der Ladenbesitzer also davon ausgeht, dass jeden Tag die gleiche Anzahl an Kunden das Geschäft betritt, wären das 50 Kunden pro Tag.

Schritt 2: Führen Sie den Chi-Quadrat-Anpassungstest durch.

Als nächstes führen wir den Chi-Quadrat-Anpassungstest durch. Drücken Sie Stat und scrollen Sie dann zu TESTS . Scrollen Sie dann nach unten zu X ² GOF-Test und drücken Sie die Eingabetaste .

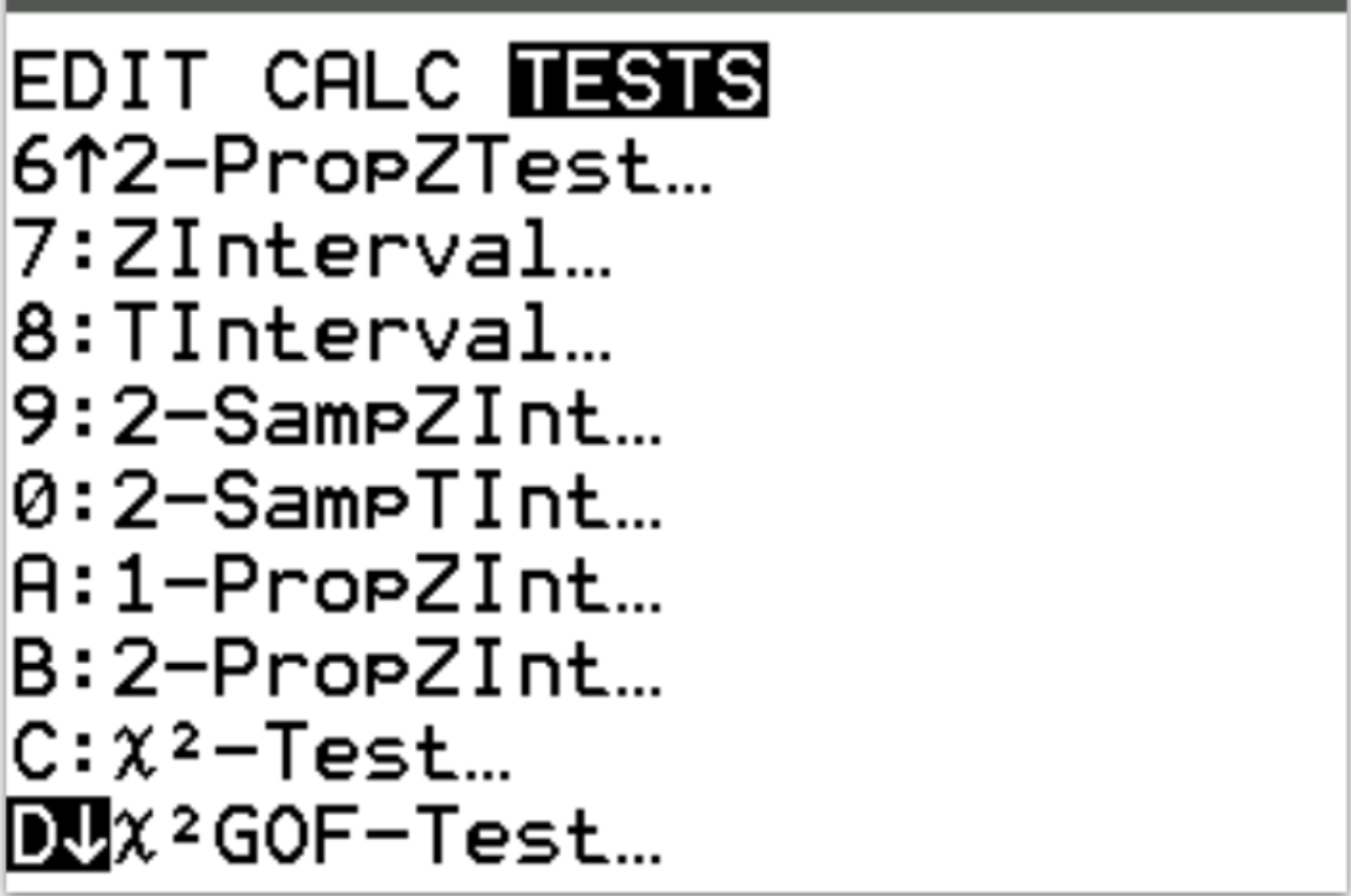
Wählen Sie für Observed die Liste L1 aus. Wählen Sie für Erwartet die Liste L2 aus. Geben Sie für df (Freiheitsgrade) #categories – 1 ein. In unserem Fall haben wir 5-1 = 4. Markieren Sie dann Berechnen und drücken Sie die Eingabetaste .

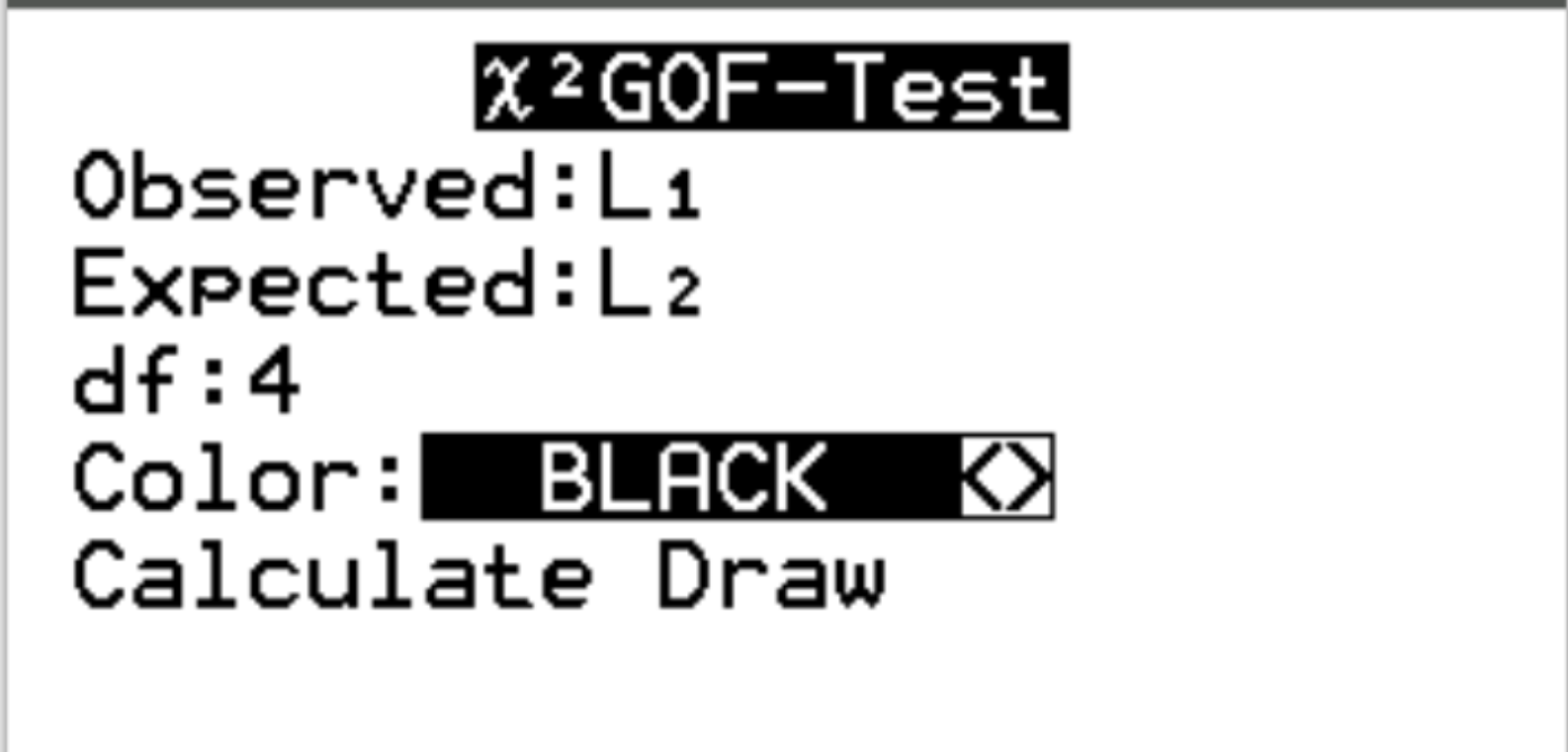
Es erscheint automatisch folgende Ausgabe:

Schritt 3: Interpretieren Sie die Ergebnisse.

Die ^X2- Teststatistik für den Test beträgt 4,36 und der entsprechende p-Wert beträgt 0,3595 . Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Das bedeutet, dass uns nicht genügend Beweise dafür vorliegen, dass sich die tatsächliche Kundenverteilung von der vom Ladenbesitzer gemeldeten unterscheidet.