So führen sie einen chi-quadrat-anpassungstest in spss durch

Mithilfe eines Chi-Quadrat-Anpassungstests wird ermittelt, ob eine kategoriale Variable einer hypothetischen Verteilung folgt oder nicht.

In diesem Tutorial wird erläutert, wie Sie in SPSS einen Chi-Quadrat-Anpassungstest durchführen.

Beispiel: Chi-Quadrat-Anpassungstest in SPSS

Ein Ladenbesitzer sagt, dass an jedem Tag der Woche gleich viele Kunden in sein Geschäft kommen. Um diese Hypothese zu testen, erfasst ein Forscher die Anzahl der Kunden, die in einer bestimmten Woche in den Laden kommen, und stellt Folgendes fest:

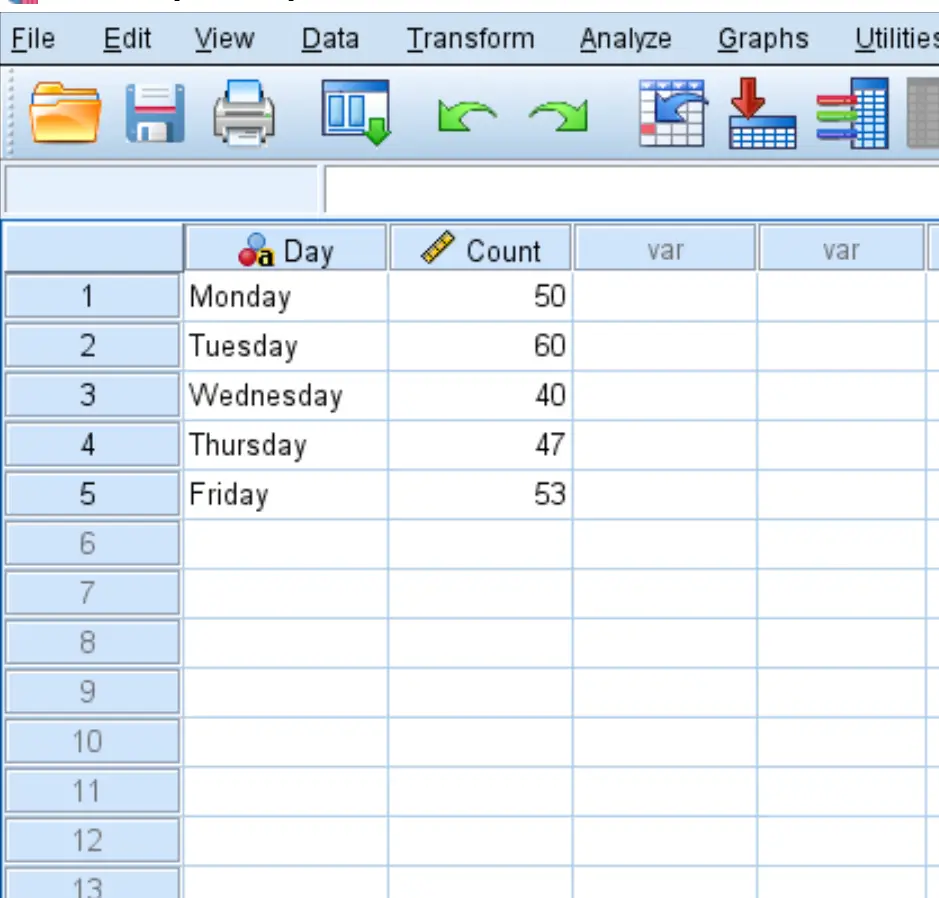
• Montag: 50 Kunden
• Dienstag: 60 Kunden
• Mittwoch: 40 Kunden
• Donnerstag: 47 Kunden
• Freitag: 53 Kunden

Führen Sie die folgenden Schritte aus, um in SPSS einen Chi-Quadrat-Anpassungstest durchzuführen und festzustellen, ob die Daten mit der Behauptung des Ladenbesitzers übereinstimmen.

Schritt 1: Geben Sie die Daten ein.

Geben Sie zunächst die Daten im folgenden Format in SPSS ein:

Schritt 2: Beschwerte Boxen verwenden.

Damit der Test korrekt funktioniert, müssen wir SPSS mitteilen, dass die Variable „Tag“ mit der Variable „Anzahl“ gewichtet werden soll.

Klicken Sie auf die Registerkarte „Daten“ und dann auf „Fälle gewichten“ :

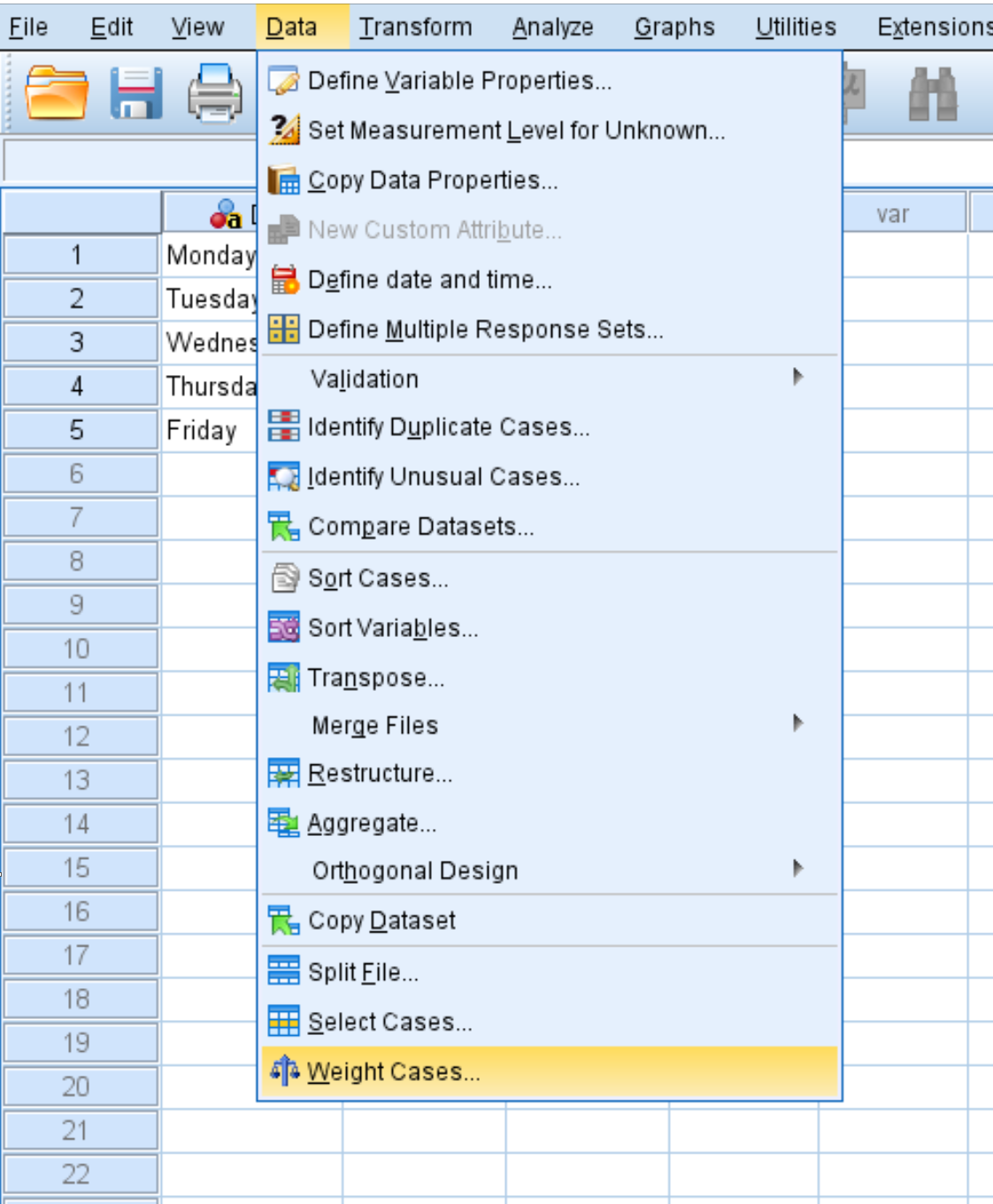
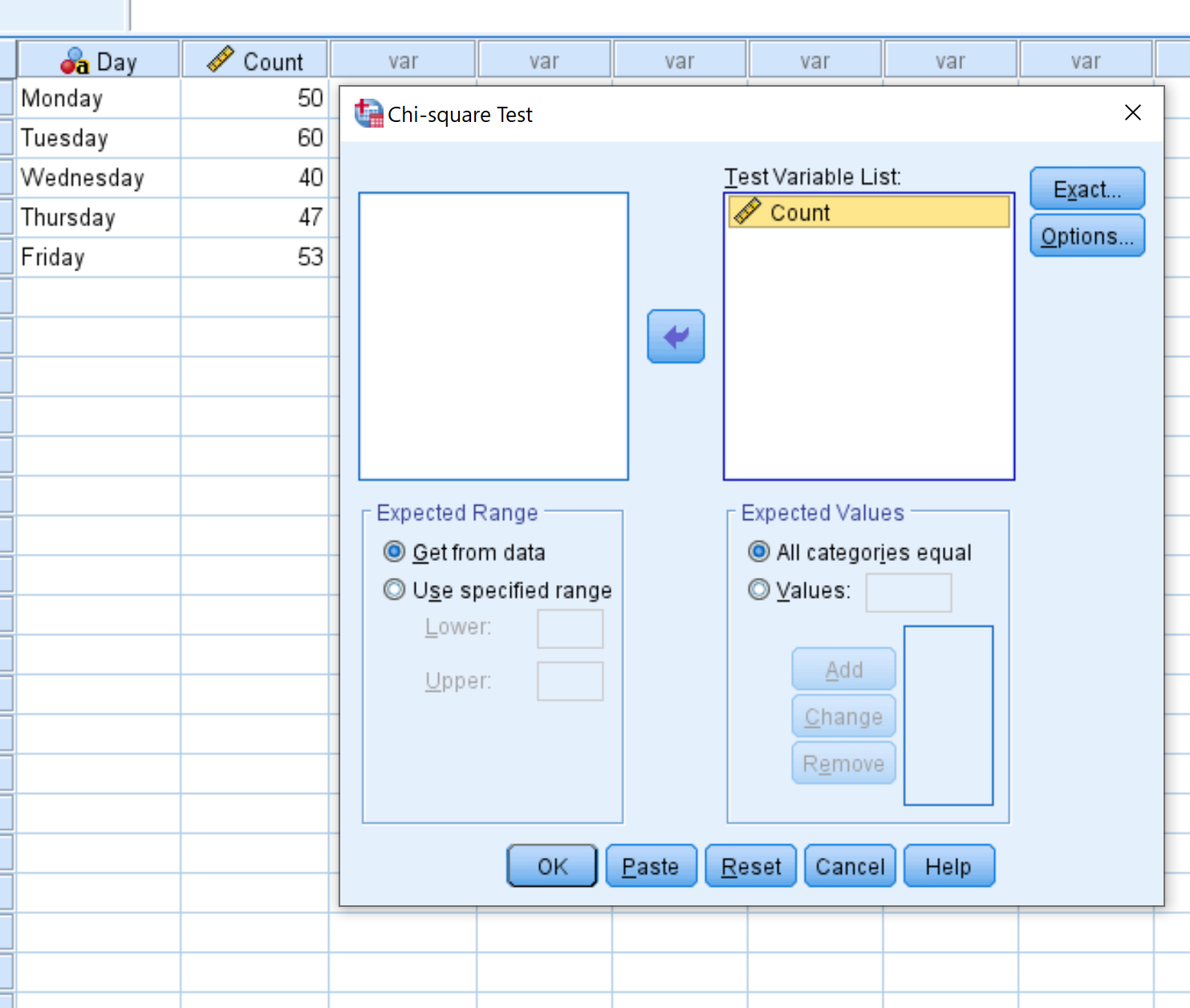
Ziehen Sie im neuen Fenster, das angezeigt wird, die Variable „Anzahl “ in den Bereich mit der Bezeichnung „Liste der Testvariablen“. Klicken Sie dann auf OK .

Schritt 3: Führen Sie den Chi-Quadrat-Anpassungstest durch.

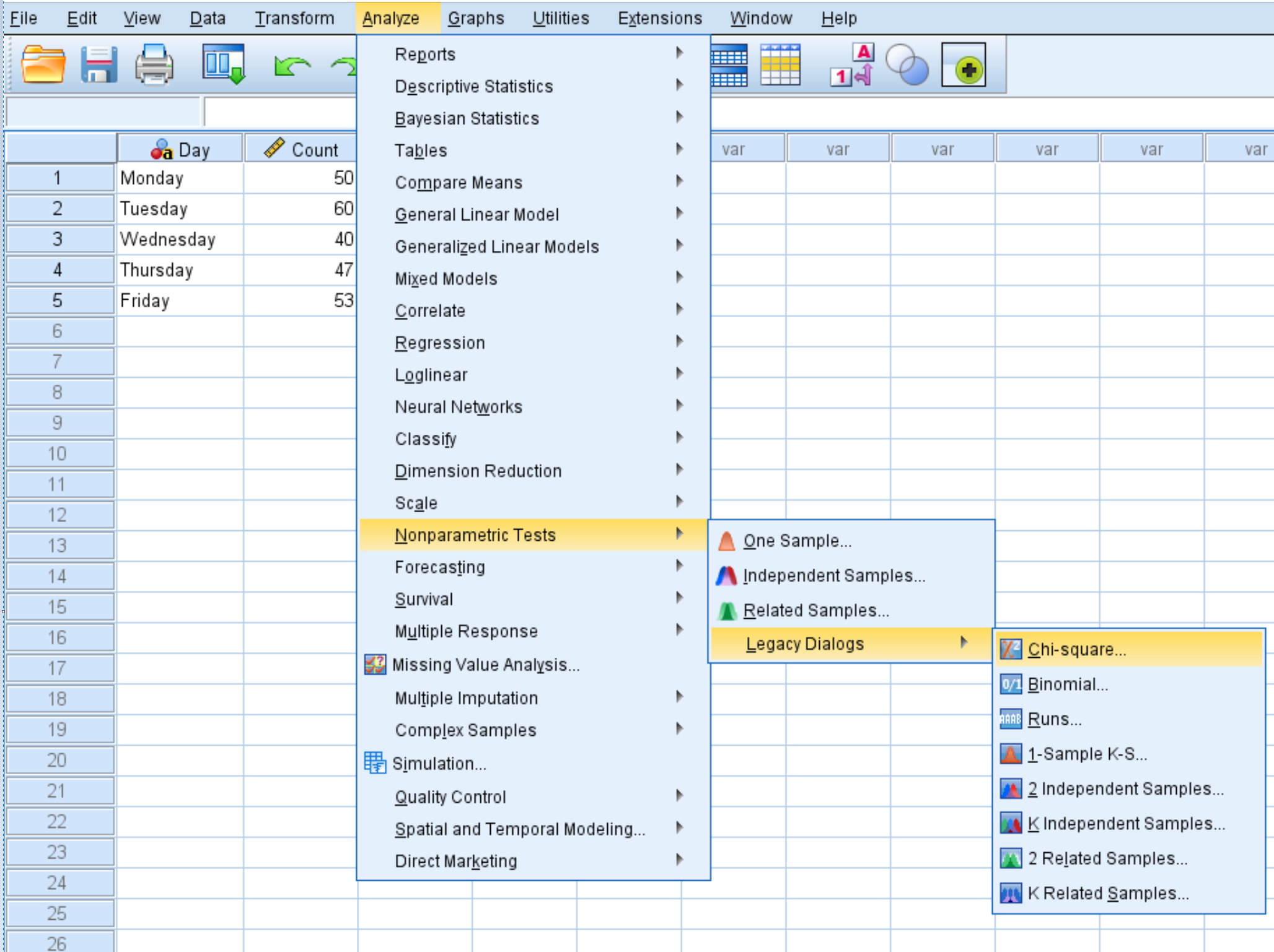
Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Nichtparametrische Tests“ , dann auf „Legacy Dialogs“ und dann auf „Chi-Quadrat “:

Ziehen Sie im neuen Fenster, das angezeigt wird, die Variable „Anzahl “ in den Bereich mit der Bezeichnung „Liste der Testvariablen“.

Lassen Sie die Markierung neben „Alle Kategorien gleich“ aktiviert, da jede unserer Kategorien (d. h. Wochentage) jeden Tag die gleiche erwartete Besucherzahl hat. Klicken Sie dann auf OK .

Schritt 4: Interpretieren Sie die Ergebnisse .

Sobald Sie auf „OK“ klicken, werden die Ergebnisse des Chi-Quadrat-Anpassungstests angezeigt:

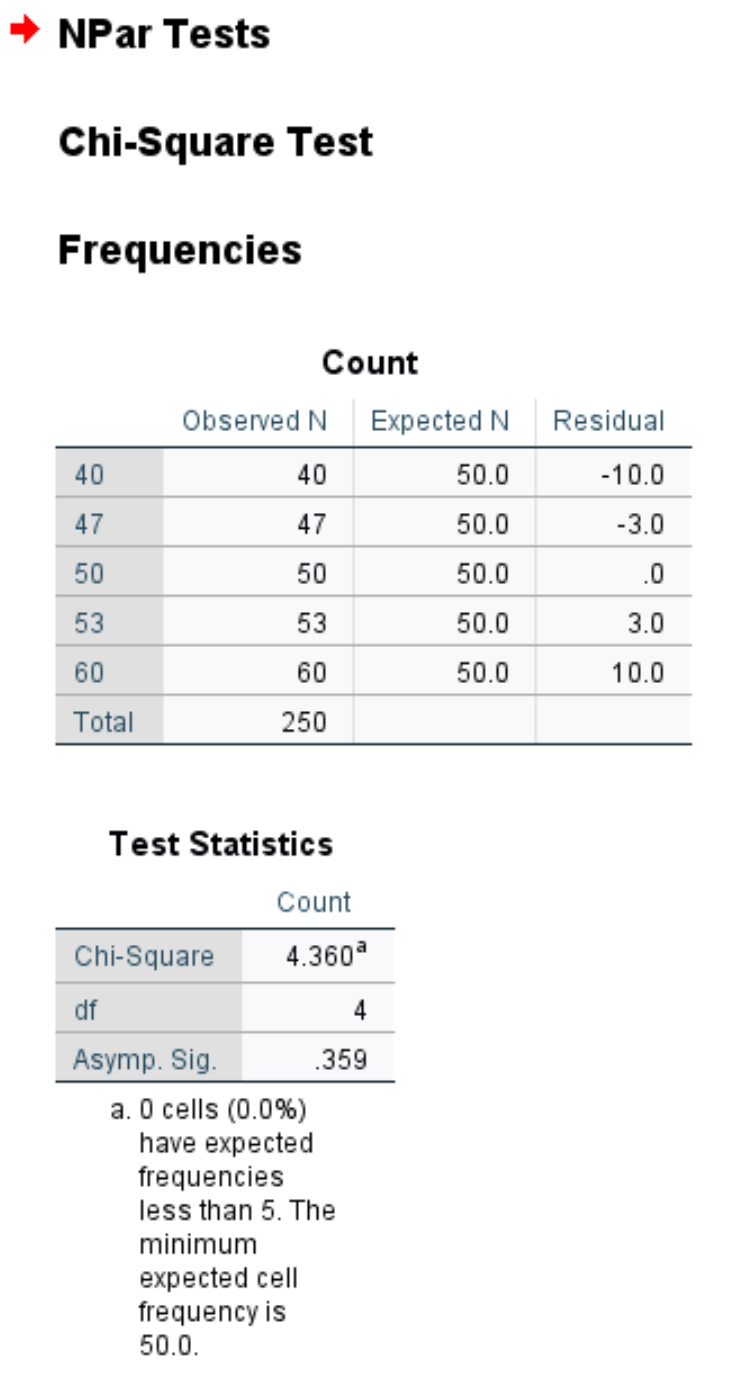
Die erste Tabelle zeigt die beobachtete und erwartete Anzahl von Kunden an jedem Wochentag sowie den Rest (dh die Differenz) zwischen beobachteter und erwarteter Anzahl.

Die zweite Tabelle zeigt die folgenden Zahlen:

Chi-Quadrat: Die Chi-Quadrat-Teststatistik, die 4,36 beträgt.

df: Die Freiheitsgrade, berechnet als #categories-1 = 5-1 = 4.

Asymp. Sig: Der p-Wert, der einem Chi-Quadrat-Wert von 4,36 mit 4 Freiheitsgraden entspricht, also 0,359. Dieser Wert kann auch mit dem Chi-Quadrat-Score-zu-P-Wert-Rechner ermittelt werden.

Da der p-Wert (0,359) nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Das bedeutet, dass uns nicht genügend Beweise dafür vorliegen, dass sich die tatsächliche Kundenverteilung von der vom Ladenbesitzer gemeldeten unterscheidet.