Chi-quadrat-verteilung
In diesem Artikel wird erklärt, was die Chi-Quadrat-Verteilung ist und wofür sie verwendet wird. Darüber hinaus finden Sie das Chi-Quadrat-Verteilungsdiagramm und seine Eigenschaften.
Was ist die Chi-Quadrat-Verteilung?
Die Chi-Quadrat-Verteilung ist eine Wahrscheinlichkeitsverteilung, deren Symbol χ² ist. Genauer gesagt ist die Chi-Quadrat-Verteilung die Summe des Quadrats von k unabhängigen Zufallsvariablen mit einer Normalverteilung.
Somit hat die Chi-Quadrat-Verteilung k Freiheitsgrade. Daher hat eine Chi-Quadrat-Verteilung so viele Freiheitsgrade wie die Summe der Quadrate der normalverteilten Variablen, die sie darstellt.
![Rendered by QuickLaTeX.com \displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9ea0bf7a87071883ceae5e419bae9e71_l3.png)
Die Chi-Quadrat-Verteilung wird auch als Pearson-Verteilung bezeichnet.
Es ist zu beachten, dass die Chi-Quadrat-Verteilung ein Sonderfall der Gamma-Verteilung ist.
Die Chi-Quadrat-Verteilung wird häufig bei statistischen Schlussfolgerungen verwendet, beispielsweise beim Testen von Hypothesen und bei Konfidenzintervallen. Wir werden unten sehen, welche Anwendungen diese Art von Wahrscheinlichkeitsverteilung sind.
Chi-Quadrat-Verteilungsdiagramm
Sobald wir die Definition der Chi-Quadrat-Verteilung sehen, werden wir mehrere Beispiele dieser Art von Verteilung grafisch dargestellt sehen. Unten sehen Sie also, wie das Wahrscheinlichkeitsdiagramm der Chi-Quadrat-Verteilung je nach Freiheitsgrad variiert.
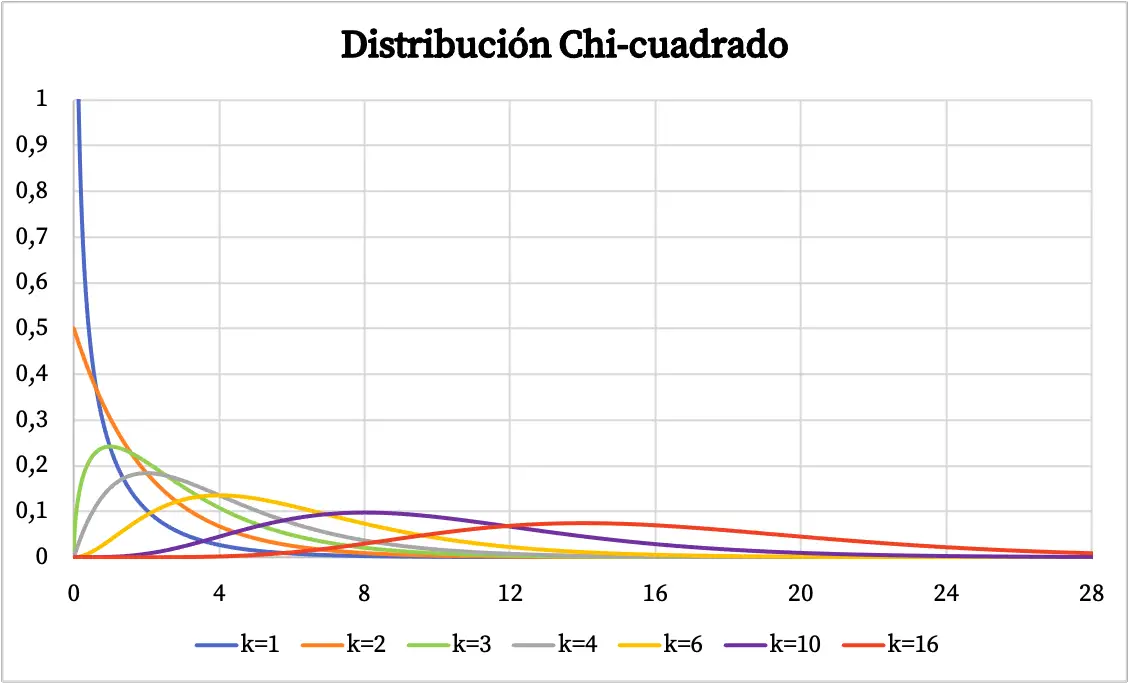
Die Dichtefunktion der Chi-Quadrat-Verteilung ist in der obigen Grafik dargestellt. Andererseits sieht das Diagramm der kumulativen Chi-Quadrat-Wahrscheinlichkeitsverteilungsfunktion wie folgt aus:
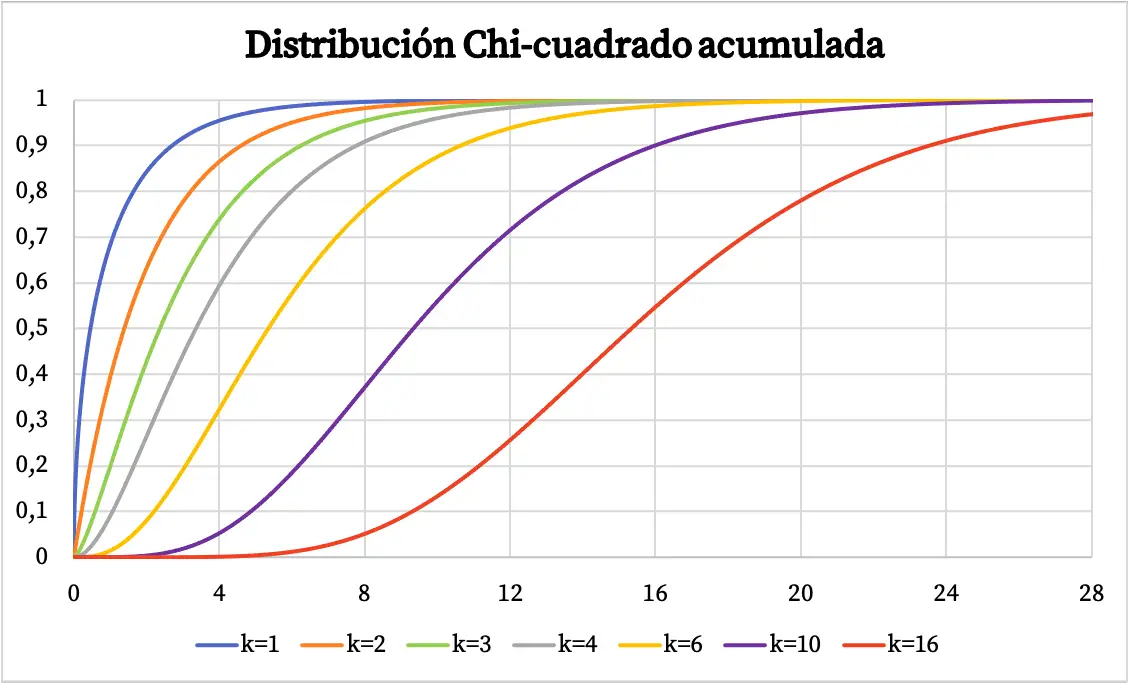
Merkmale der Chi-Quadrat-Verteilung
In diesem Abschnitt werden wir die wichtigsten Eigenschaften der Chi-Quadrat-Verteilung im Zusammenhang mit Wahrscheinlichkeitstheorie und Statistik sehen.
- Der Mittelwert einer Chi-Quadrat-Verteilung entspricht ihren Freiheitsgraden.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8a7926aa60ec788064c47a5a34e641ab_l3.png)
- Die Varianz einer Chi-Quadrat-Verteilung entspricht dem Doppelten der Freiheitsgrade der Verteilung.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-cffd659f19d8ed8260fcaf53dc6dd83f_l3.png)
- Der Modus einer Chi-Quadrat-Verteilung ist zwei Einheiten kleiner als ihre Freiheitsgrade, solange die Verteilung mehr als einen Freiheitsgrad hat.
![]()
- Die Dichtefunktion der Chi-Quadrat-Verteilung ist Null, wenn x=0. Für Werte von x größer als 0 wird die Dichtefunktion einer Chi-Quadrat-Verteilung jedoch durch die folgende Formel definiert:
![]()
- Die kumulative Verteilungsfunktion der Chi-Quadrat-Verteilung wird durch die folgende Formel bestimmt:
![]()
- Der Schiefekoeffizient der Chi-Quadrat-Verteilung ist die Quadratwurzel des Quotienten von acht dividiert durch die Anzahl der Freiheitsgrade der Verteilung.
![]()
- Die Kurtosis der Chi-Quadrat-Verteilung wird mit dem folgenden Ausdruck berechnet:
![]()
- Aufgrund des zentralen Grenzwertsatzes kann die Chi-Quadrat-Verteilung durch eine Normalverteilung angenähert werden, wenn k groß genug ist.
![]()
Anwendungen der Chi-Quadrat-Verteilung
Die Chi-Quadrat-Verteilung hat in der Statistik viele verschiedene Anwendungen. Tatsächlich gibt es sogar den Chi-Quadrat-Test, mit dem die Unabhängigkeit zwischen Variablen und die Güte der Anpassung an eine theoretische Verteilung überprüft werden. Beispielsweise kann der Chi-Quadrat-Test verwendet werden, um zu bestimmen, ob die Daten einer Stichprobe einer Poisson-Verteilung entsprechen.
Bei der linearen Regressionsanalyse wird die Chi-Quadrat-Verteilung auch verwendet, um den Mittelwert einer normalverteilten Grundgesamtheit und die Steigung der Studienlinie der linearen Regression zu schätzen.
Schließlich ist auch die Chi-Quadrat-Verteilung durch ihre Beziehung zur Snedecor-F-Verteilung an der Varianzanalyse beteiligt.