So führen sie einen chow-test in r durch

Mit einem Chow-Test wird getestet, ob die Koeffizienten zweier unterschiedlicher Regressionsmodelle auf unterschiedlichen Datensätzen gleich sind.

Dieser Test wird typischerweise im Bereich der Ökonometrie mit Zeitreihendaten verwendet, um festzustellen, ob zu einem bestimmten Zeitpunkt ein Strukturbruch in den Daten vorliegt.

Dieses Tutorial bietet ein schrittweises Beispiel für die Durchführung eines Chow-Tests in R.

Schritt 1: Erstellen Sie die Daten

Zuerst erstellen wir gefälschte Daten:

 #create data
data <- data.frame(x = c(1, 1, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, 8, 9, 10, 10,
                         11, 12, 12, 13, 14, 15, 15, 16, 17, 18, 18, 19, 20, 20),
                   y = c(3, 5, 6, 10, 13, 15, 17, 14, 20, 23, 25, 27, 30, 30, 31,
                         33, 32, 32, 30, 32, 34, 34, 37, 35, 34, 36, 34, 37, 38, 36))

#view first six rows of data
head(data)

  xy
1 1 3
2 1 5
3 2 6
4 3 10
5 4 13
6 4 15

Schritt 2: Visualisieren Sie die Daten

Als Nächstes erstellen wir ein einfaches Streudiagramm zur Visualisierung der Daten:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(data, aes (x = x, y = y)) +
    geom_point(col=' steelblue ', size= 3 )

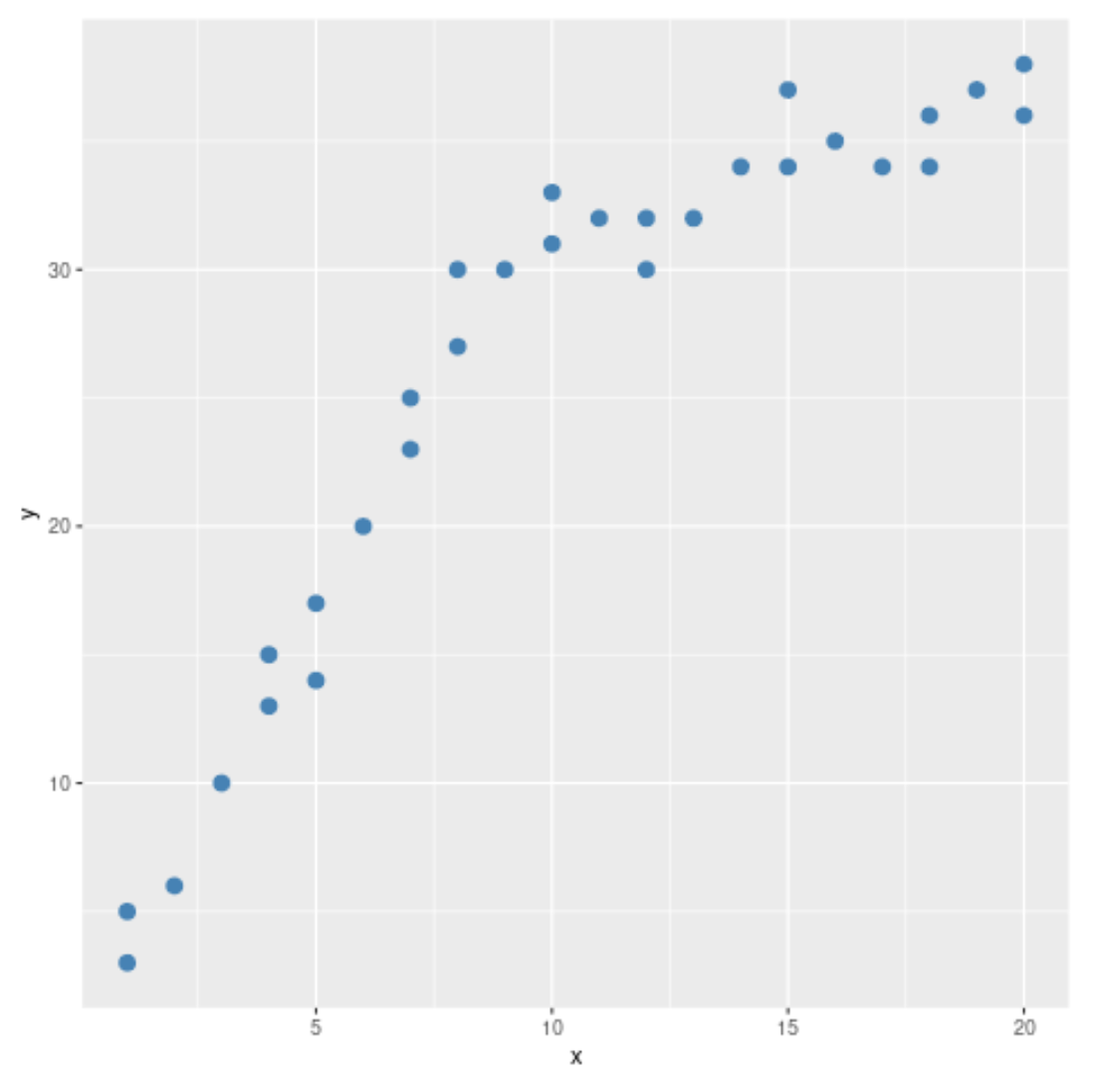
Aus dem Streudiagramm können wir erkennen, dass sich das Muster in den Daten bei x = 10 zu ändern scheint. Daher können wir den Chow-Test durchführen, um festzustellen, ob es bei x = 10 einen strukturellen Bruchpunkt in den Daten gibt.

Schritt 3: Führen Sie den Chow-Test durch

Wir können die sctest- Funktion aus dem strucchange- Paket verwenden, um einen Chow-Test durchzuführen:

 #load strucchange package
library (strucchange)

#perform Chow test
sctest(data$y ~ data$x, type = " Chow ", point = 10 )

	Chow test

data: data$y ~ data$x
F = 110.14, p-value = 2.023e-13

Aus dem Testergebnis können wir erkennen:

• F-Test- Statistik : 110,14
• p-Wert: <.0000

Da der p-Wert kleiner als 0,05 ist, können wir die Nullhypothese des Tests ablehnen. Das bedeutet, dass wir genügend Beweise dafür haben, dass in den Daten ein struktureller Bruchpunkt vorhanden ist.

Mit anderen Worten: Zwei Regressionslinien können das Modell effektiver in die Daten einpassen als eine einzelne Regressionslinie.