Was ist cochrans q-test? (definition & #038; beispiel)

Der Q-Test von Cochran ist ein statistischer Test, der verwendet wird, um zu bestimmen, ob der Anteil der „Erfolge“ in drei oder mehr Gruppen gleich ist, in denen in jeder Gruppe dieselben Personen vorkommen.

Beispielsweise können wir den Q-Test von Cochran verwenden, um festzustellen, ob der Anteil der Schüler, die einen Test bestehen, gleich ist, wenn drei verschiedene Lerntechniken angewendet werden.

Schritte zur Durchführung des Cochran-Q-Tests

Der Q-Test von Cochran verwendet die folgenden Null- und Alternativhypothesen:

Nullhypothese (H ₀ ): Der Anteil der „Erfolge“ ist in allen Gruppen gleich

Alternativhypothese ( _HA ): Der Anteil der „Erfolge“ ist in mindestens einer der Gruppen unterschiedlich

Die Teststatistik wird wie folgt berechnet:

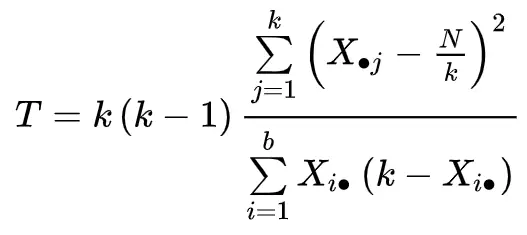
Gold:

• k: Die Anzahl der Behandlungen (oder „Gruppen“)
• Xj: die Summe der Spalte für die ^j-te Behandlung
• b: Die Anzahl der Blöcke
• Xi. : Die Summe der Zeile für den ^i-ten Block
• N: Die Gesamtsumme

Die T- Teststatistik folgt einer Chi-Quadrat-Verteilung mit k-1 Freiheitsgraden.

Wenn der mit der Teststatistik verbundene p-Wert unter einem bestimmten Signifikanzniveau liegt (z. B. α = 0,05), können wir die Nullhypothese ablehnen und daraus schließen, dass wir über ausreichende Beweise verfügen, um zu sagen, dass der Anteil der „Erfolge“ unterschiedlich ist mindestens eine der Gruppen.

Beispiel: Cochrans Q-Test

Angenommen, ein Forscher möchte wissen, ob drei verschiedene Lerntechniken zu unterschiedlichen Erfolgsquoten bei Studierenden führen.

Um dies zu testen, rekrutiert sie 20 Studenten, die jeweils eine Prüfung mit gleichem Schwierigkeitsgrad ablegen und dabei drei verschiedene Lerntechniken anwenden. Die Ergebnisse sind unten dargestellt:

Zur Durchführung des Cochran-Q-Tests können wir Statistiksoftware verwenden, da die manuelle Durchführung mühsam sein kann.

Hier ist der Code, mit dem wir diesen Datensatz erstellen und Cochrans Q-Test in der statistischen Programmiersprache R durchführen können:

 #load DescTools package
library (DescTools)

#create dataset
df <- data.frame(student= rep (1:20, each = 3 ),
                 technique= rep (c('A', 'B', 'C'), times= 20 ),
                 outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1,
                           1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
                           1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1,
                           1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1))

#perform Cochran's Q test
CochranQTest(outcome ~ technique| student, data=df)

	Cochran's Q test

data: outcome and technique and student
Q = 0.33333, df = 2, p-value = 0.8465

Aus dem Testergebnis können wir folgendes beobachten:

• Die Teststatistik beträgt 0,333
• Der entsprechende p-Wert beträgt 0,8465

Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.

Das bedeutet, dass uns nicht genügend Belege dafür vorliegen, dass die von Studierenden verwendete Lerntechnik zu unterschiedlichen Erfolgsquoten führt.