So berechnen sie cohens d in excel

Wenn wir in der Statistik feststellen möchten, ob zwischen zwei Gruppen ein signifikanter Unterschied besteht oder nicht, führen wir häufig einen Hypothesentest durch, der einen p-Wert ergibt.

Wenn dieser p-Wert unter einem bestimmten Signifikanzniveau liegt (übliche Werte sind 0,10, 0,05 und 0,01), schließen wir daraus, dass ein statistisch signifikanter Unterschied zwischen den beiden Gruppen besteht.

Während uns ein p-Wert jedoch sagen kann, ob zwischen zwei Gruppen ein statistisch signifikanter Unterschied besteht oder nicht, kann uns eine Effektgröße sagen, wie groß dieser Unterschied tatsächlich ist.

Eines der gebräuchlichsten Maße für die Effektstärke ist Cohens d , das wie folgt berechnet wird:

Cohens d = ( x ₁ – x ₂ ) / gepoolte SD

Gold:

• x ₁ = Durchschnitt der Gruppe 1
• x ₂ = Durchschnitt der Gruppe 2
• Gruppierte SD = √ (s ₁ ² + s ₂ ² ) / 2

In diesem Tutorial wird erklärt, wie man Cohens d in Excel berechnet.

Beispiel: Cohens d in Excel

Führen Sie die folgenden Schritte aus, um Cohens d in Excel zu berechnen.

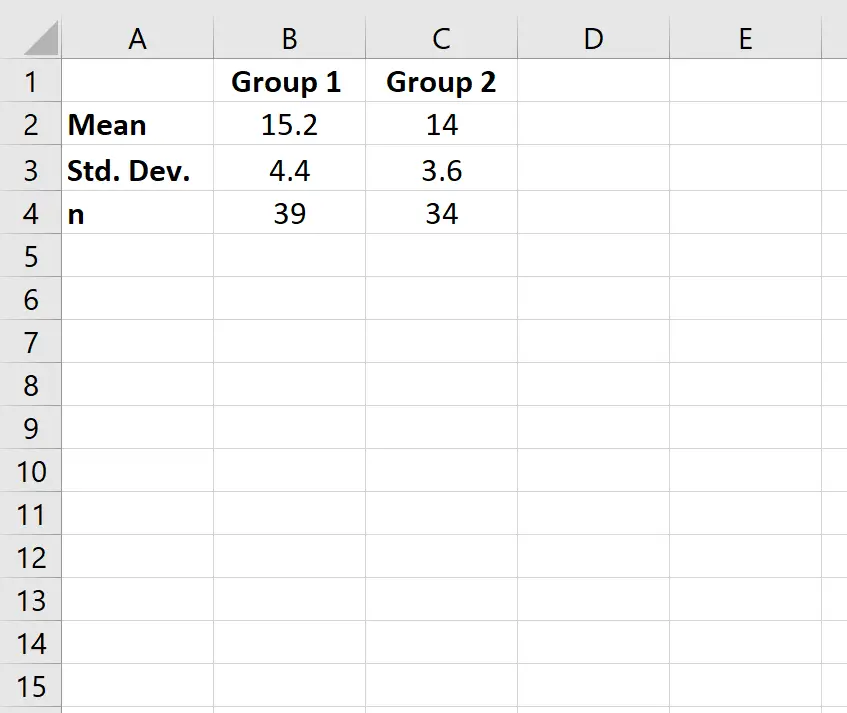
Schritt 1: Geben Sie die Daten ein.

Zunächst geben wir die Werte für Mittelwert, Standardabweichung und Stichprobengröße (n) für zwei Gruppen ein.

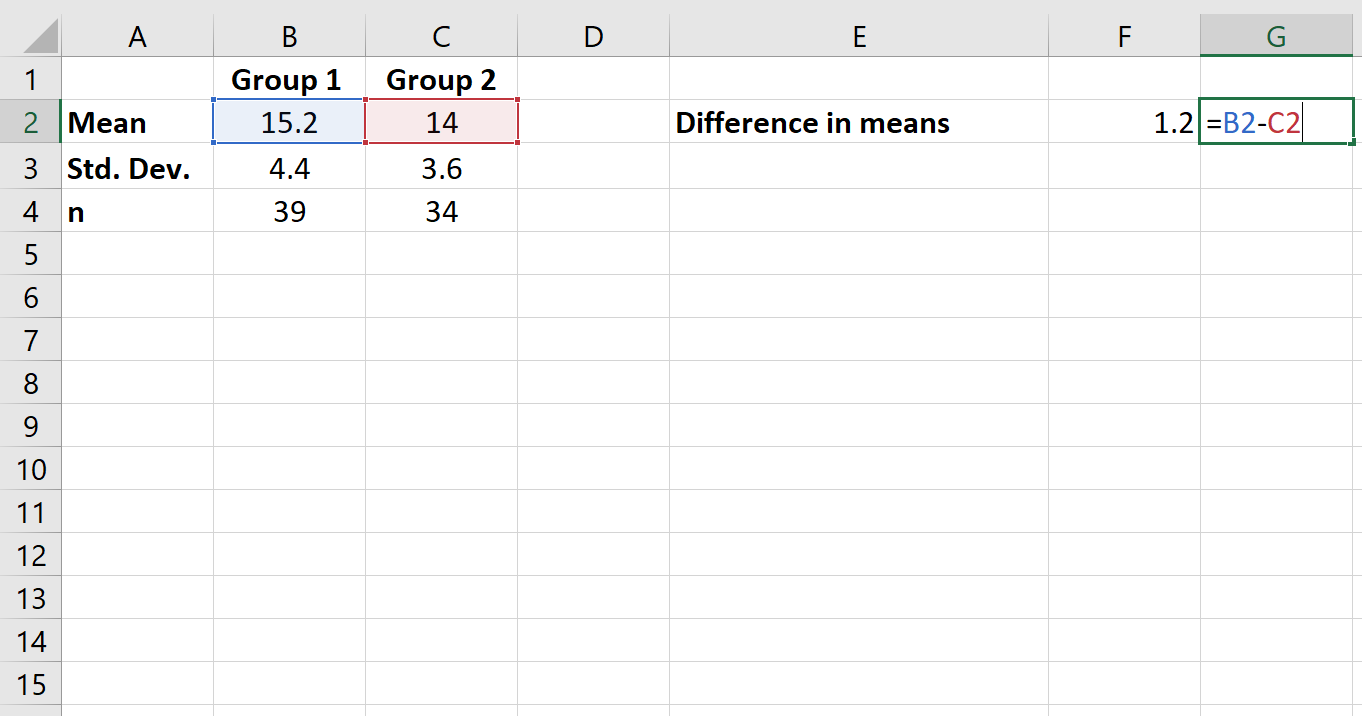
Schritt 2: Berechnen Sie die Mittelwertdifferenz.

Als nächstes berechnen wir die Differenz zwischen den Gruppenmitteln.

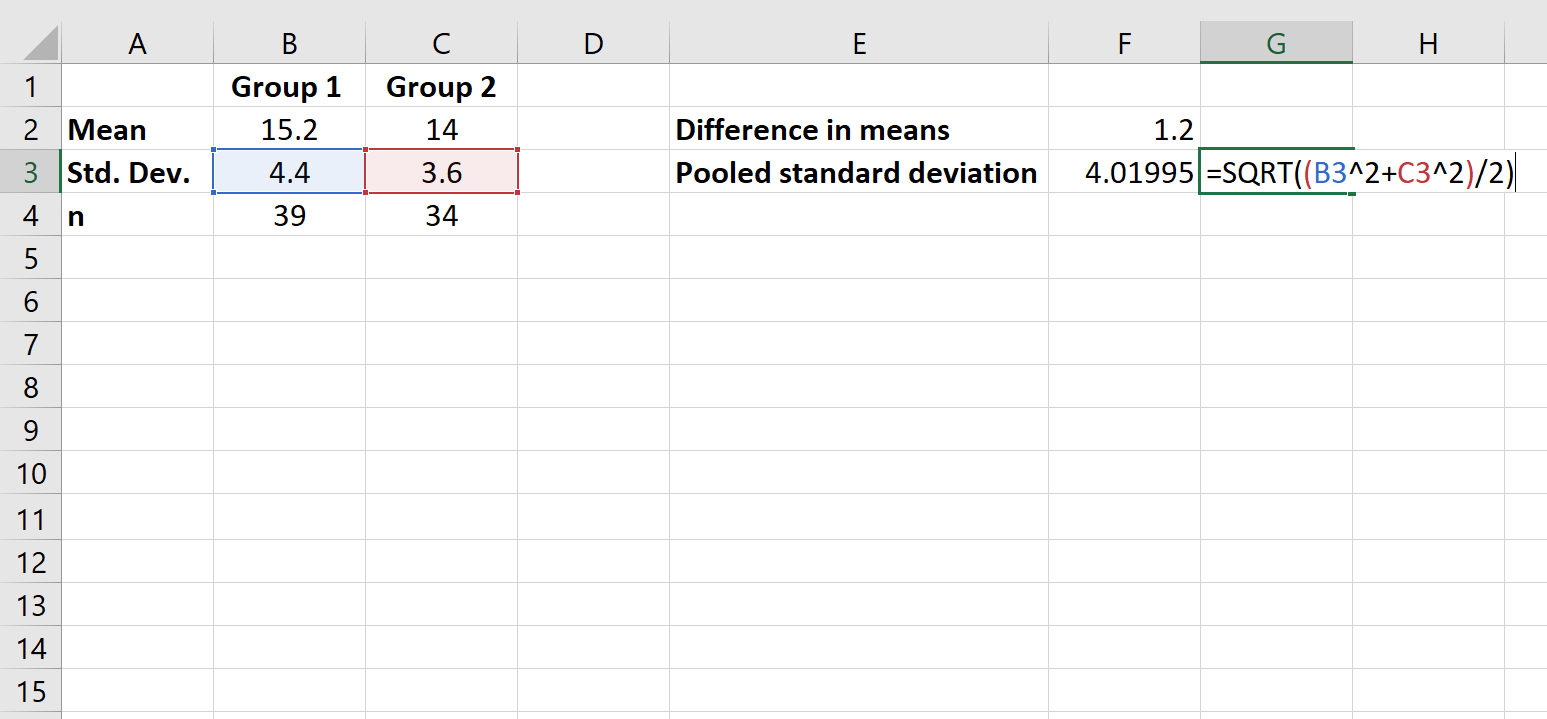
Schritt 3: Berechnen Sie die gepoolte Standardabweichung.

Als nächstes berechnen wir die gepoolte Standardabweichung.

Schritt 4: Berechnen Sie Cohens d.

Abschließend berechnen wir Cohens d.

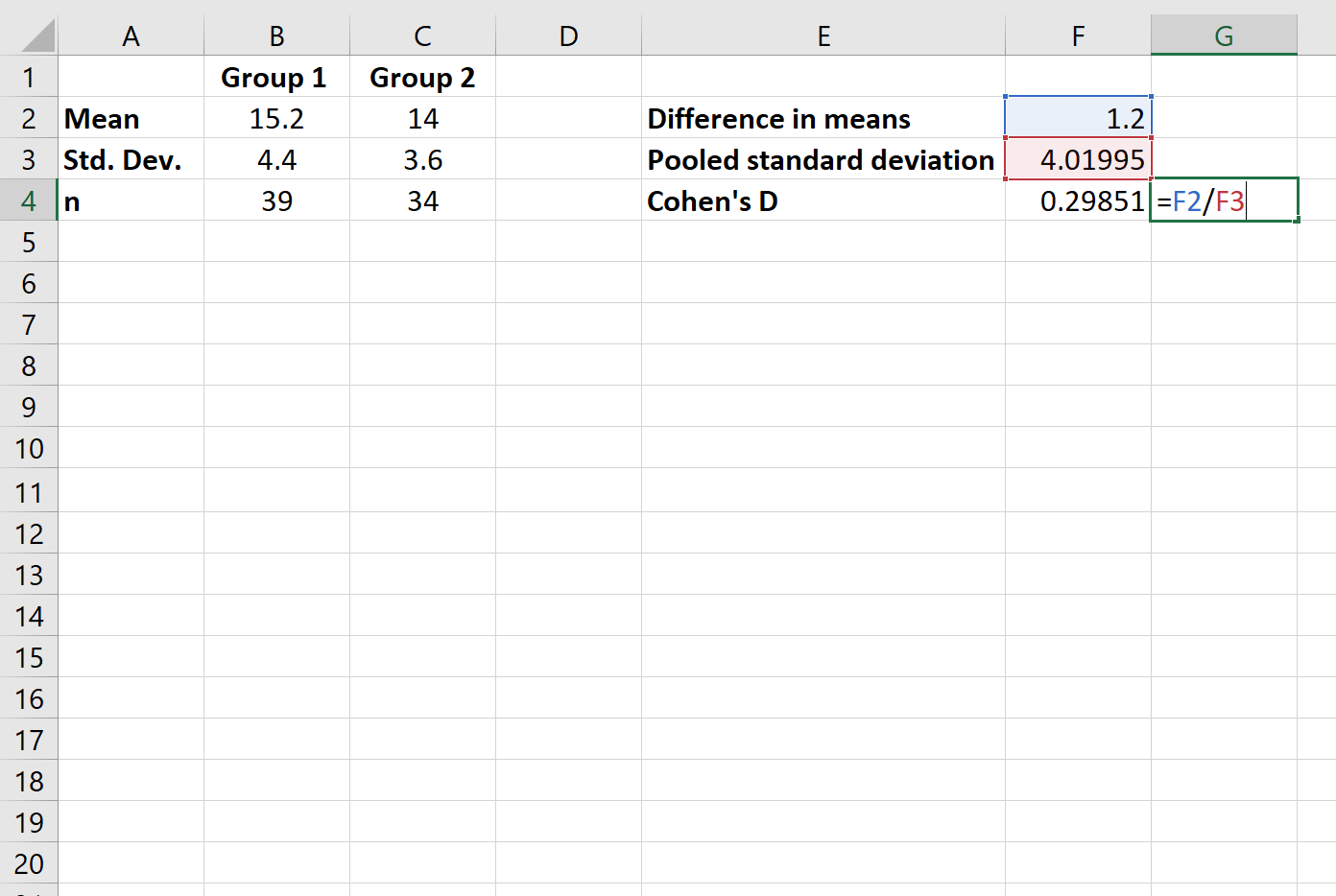
Cohens d beträgt für dieses Beispiel 0,29851 .

Wie ist Cohens d zu interpretieren?

Im Allgemeinen ist Cohens d wie folgt zu interpretieren:

• 0,2 = Kleine Effektgröße
• 0,5 = mittlere Effektstärke
• 0,8 = Große Effektgröße

In unserem Beispiel würde eine Effektgröße von 0,29851 wahrscheinlich als kleine Effektgröße angesehen werden.

Dies bedeutet, dass, obwohl der Unterschied zwischen den Mittelwerten der beiden Gruppen statistisch signifikant unterschiedlich ist, der tatsächliche Unterschied zwischen den Mittelwerten der Gruppen unbedeutend ist.