So überprüfen sie anova-annahmen
Eine einfaktorielle ANOVA ist ein statistischer Test, mit dem ermittelt wird, ob zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen ein signifikanter Unterschied besteht.
Hier ist ein Beispiel dafür, wann wir eine einfaktorielle ANOVA verwenden könnten:
Sie teilen eine Klasse mit 90 Schülern nach dem Zufallsprinzip in drei Gruppen zu je 30 Personen auf. Jede Gruppe verwendet einen Monat lang eine andere Lerntechnik, um sich auf eine Prüfung vorzubereiten. Am Ende des Monats legen alle Studierenden die gleiche Prüfung ab.
Sie möchten wissen, ob die Lerntechnik einen Einfluss auf die Prüfungsergebnisse hat. Sie führen also eine einfaktorielle ANOVA durch, um festzustellen, ob zwischen den Durchschnittswerten der drei Gruppen ein statistisch signifikanter Unterschied besteht.
Bevor wir eine einfaktorielle ANOVA durchführen können, müssen wir zunächst überprüfen, ob drei Annahmen erfüllt sind.
1. Normalität – Jede Stichprobe wurde aus einer normalverteilten Grundgesamtheit gezogen.
2. Gleiche Varianzen – Die Varianzen der Grundgesamtheiten, aus denen die Stichproben gezogen werden, sind gleich.
3. Unabhängigkeit – Die Beobachtungen innerhalb jeder Gruppe sind unabhängig voneinander und die Beobachtungen innerhalb der Gruppen wurden durch Zufallsstichproben ermittelt.
Wenn diese Annahmen nicht erfüllt sind, sind die Ergebnisse unserer einfaktoriellen ANOVA möglicherweise nicht zuverlässig.
In diesem Artikel erklären wir, wie Sie diese Annahmen überprüfen und was zu tun ist, wenn eine davon verletzt wird.
Annahme Nr. 1: Normalität
ANOVA geht davon aus, dass jede Stichprobe aus einer normalverteilten Grundgesamtheit stammt.
So überprüfen Sie diese Hypothese in R:
Um diese Hypothese zu überprüfen, können wir zwei Ansätze verwenden:
- Überprüfen Sie die Hypothese visuell mithilfe von Histogrammen oder QQ-Diagrammen .
- Überprüfen Sie die Hypothese mithilfe formaler statistischer Tests wie Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre oder D’Agostino-Pearson.
Angenommen, wir rekrutieren 90 Personen für die Teilnahme an einem Abnehmexperiment, bei dem wir 30 Personen nach dem Zufallsprinzip dazu auffordern, einen Monat lang entweder Programm A, Programm B oder Programm C zu befolgen. Um zu sehen, ob das Programm einen Einfluss auf die Gewichtsabnahme hat, möchten wir eine einfaktorielle ANOVA durchführen. Der folgende Code zeigt, wie die Normalitätsannahme mithilfe von Histogrammen, QQ-Diagrammen und einem Shapiro-Wilk-Test überprüft wird.
1. Passen Sie das ANOVA-Modell an.
#make this example reproducible
set.seed(0)
#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
weight_loss = c(runif(30, 0, 3),
runif(30, 0, 5),
runif(30, 1, 7)))
#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)
2. Erstellen Sie ein Histogramm der Antwortwerte.
#create histogram
hist(data$weight_loss)
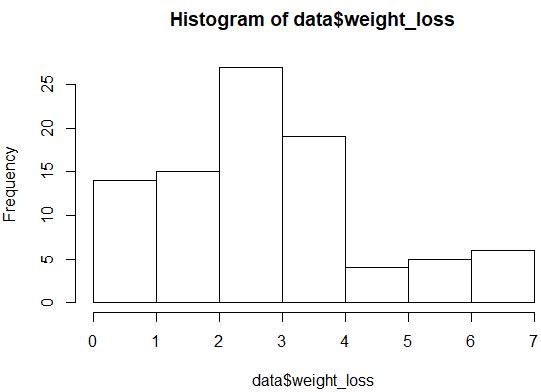
Die Verteilung sieht nicht besonders normalverteilt aus (z. B. ist sie nicht „glockenförmig“), aber wir können auch ein QQ-Diagramm erstellen, um einen anderen Blick auf die Verteilung zu werfen.
3. Erstellen Sie ein QQ-Diagramm der Residuen
#create QQ plot to compare this dataset to a theoretical normal distribution qqnorm(model$residuals) #add straight diagonal line to plot qqline(model$residuals)

Wenn die Datenpunkte in einem QQ-Diagramm entlang einer geraden diagonalen Linie liegen, folgt der Datensatz im Allgemeinen wahrscheinlich einer Normalverteilung. In diesem Fall können wir eine deutliche Abweichung von der Linie an den Enden erkennen, was darauf hindeuten könnte, dass die Daten nicht normalverteilt sind.
4. Führen Sie den Shapiro-Wilk-Test auf Normalität durch.
#Conduct Shapiro-Wilk Test for normality shapiro. test (data$weight_loss) #Shapiro-Wilk normality test # #data: data$weight_loss #W = 0.9587, p-value = 0.005999
Der Shapiro-Wilk-Test testet die Nullhypothese, dass die Stichproben aus einer Normalverteilung stammen, mit der Alternativhypothese, dass die Stichproben nicht aus einer Normalverteilung stammen. In diesem Fall beträgt der p-Wert des Tests 0,005999 , was niedriger ist als der Alpha-Wert von 0,05. Dies deutet darauf hin, dass die Stichproben keiner Normalverteilung folgen.
Was tun, wenn diese Annahme nicht respektiert wird:
Im Allgemeinen gilt eine einfaktorielle ANOVA als recht robust gegenüber Verletzungen der Normalitätsannahme, solange die Stichprobengrößen groß genug sind.
Wenn Sie über extrem große Stichproben verfügen, werden Ihnen außerdem statistische Tests wie der Shapiro-Wilk-Test fast immer sagen, dass Ihre Daten nicht normal sind. Aus diesem Grund ist es oft am besten, Ihre Daten visuell mithilfe von Diagrammen wie Histogrammen und QQ-Diagrammen zu überprüfen. Wenn Sie sich nur die Diagramme ansehen, können Sie eine ziemlich gute Vorstellung davon bekommen, ob die Daten normalverteilt sind oder nicht.
Wenn die Annahme der Normalität stark verletzt wird oder Sie einfach nur sehr konservativ sein möchten, haben Sie zwei Möglichkeiten:
(1) Transformieren Sie die Antwortwerte Ihrer Daten, sodass die Verteilungen normaler verteilt sind.
(2) Führen Sie einen äquivalenten nichtparametrischen Test durch, beispielsweise einen Kruskal-Wallis-Test , der keine Normalitätsannahme erfordert.
Annahme Nr. 2: gleiche Varianz
ANOVA geht davon aus, dass die Varianzen der Populationen, aus denen die Stichproben gezogen werden, gleich sind.
So überprüfen Sie diese Hypothese in R:
Wir können diese Hypothese in R mit zwei Ansätzen überprüfen:
- Überprüfen Sie die Hypothese visuell mithilfe von Boxplots.
- Testen Sie die Hypothese mit formalen statistischen Tests wie dem Bartlett-Test.
Der folgende Code zeigt, wie das geht, indem er denselben gefälschten Gewichtsverlustdatensatz verwendet, den wir zuvor erstellt haben.
1. Erstellen Sie Boxplots.
#Create box plots that show distribution of weight loss for each group boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)
Die Varianz des Gewichtsverlusts in jeder Gruppe kann anhand der Länge jedes Boxplots beobachtet werden. Je länger die Box ist, desto höher ist die Varianz. Wir können beispielsweise erkennen, dass die Varianz bei Teilnehmern an Programm C etwas höher ist als bei Teilnehmern an Programm A und Programm B.
2. Führen Sie den Bartlett-Test durch.
#Create box plots that show distribution of weight loss for each group bartlett. test (weight_loss ~ program, data=data) #Bartlett test of homogeneity of variances # #data: weight_loss by program #Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599
Der Bartlett-Test testet die Nullhypothese, dass die Stichproben gleiche Varianzen aufweisen, im Vergleich zur Alternativhypothese, dass die Stichproben keine gleichen Varianzen aufweisen. In diesem Fall beträgt der p-Wert des Tests 0,01599 , was niedriger ist als der Alpha-Wert von 0,05. Dies deutet darauf hin, dass nicht alle Stichproben die gleiche Varianz aufweisen.
Was tun, wenn diese Annahme nicht respektiert wird:
Im Allgemeinen gilt eine einfaktorielle ANOVA als ziemlich robust gegenüber Verstößen gegen die Annahme gleicher Varianzen, solange jede Gruppe die gleiche Stichprobengröße hat.
Wenn die Stichprobengrößen jedoch nicht gleich sind und diese Annahme schwerwiegend verletzt wird, können Sie stattdessen einen Kruskal-Wallis-Test ausführen, bei dem es sich um die nichtparametrische Version der einfaktoriellen ANOVA handelt.
Annahme Nr. 3: Unabhängigkeit
ANOVA geht davon aus:
- Die Beobachtungen jeder Gruppe sind unabhängig von den Beobachtungen aller anderen Gruppen.
- Die Beobachtungen innerhalb jeder Gruppe wurden durch eine Zufallsstichprobe ermittelt.
So überprüfen Sie diese Hypothese:
Es gibt keinen formalen Test, mit dem Sie überprüfen können, ob die Beobachtungen in jeder Gruppe unabhängig sind und aus einer Zufallsstichprobe stammen. Die einzige Möglichkeit, diese Annahme zu erfüllen, ist die Verwendung eines randomisierten Designs.
Was tun, wenn diese Annahme nicht respektiert wird:
Leider können Sie nicht viel tun, wenn diese Annahme nicht erfüllt ist. Einfach ausgedrückt: Wenn die Daten so gesammelt wurden, dass die Beobachtungen in jeder Gruppe nicht unabhängig von den Beobachtungen in anderen Gruppen waren, oder wenn die Beobachtungen innerhalb jeder Gruppe nicht durch einen randomisierten Prozess gewonnen wurden, sind die ANOVA-Ergebnisse nicht zuverlässig .
Wenn diese Annahme nicht erfüllt ist, ist es am besten, das Experiment mit einem randomisierten Design neu zu erstellen.
Weiterführende Literatur:
So führen Sie eine einfaktorielle ANOVA in R durch
So führen Sie eine einfaktorielle ANOVA in Excel durch
