So analysieren sie residuen in einem anova-modell

Eine ANOVA („Varianzanalyse“) ist eine Art Modell, mit dem ermittelt wird, ob zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen ein signifikanter Unterschied besteht oder nicht.

Wenn wir ein ANOVA-Whenever-Modell an einen Datensatz anpassen, wird es immer Residuen geben – diese stellen die Differenz zwischen jeder einzelnen Beobachtung und dem Gruppenmittelwert dar, aus dem die Beobachtung stammt.

Das folgende Beispiel zeigt, wie Residuen für ein ANOVA-Modell in der Praxis berechnet werden.

Beispiel: Berechnung von Residuen in der ANOVA

Angenommen, wir rekrutieren 90 Personen für die Teilnahme an einem Abnehmexperiment, bei dem wir 30 Personen nach dem Zufallsprinzip dazu auffordern, einen Monat lang Programm A, Programm B oder Programm C zu befolgen.

Wir können eine einfaktorielle ANOVA durchführen, um festzustellen, ob es einen statistisch signifikanten Unterschied zwischen dem Gewichtsverlust aufgrund der drei Programme gibt.

Angenommen, wir berechnen den durchschnittlichen Gewichtsverlust der an den einzelnen Programmen teilnehmenden Personen wie folgt:

• Programm A : 1,58 Pfund
• Programm B : 2,56 Pfund
• Programm C : 4,13 Pfund

Die Residuen des ANOVA-Modells wären die Differenz zwischen dem Gewichtsverlust jedes Einzelnen und dem durchschnittlichen Gewichtsverlust seines Programms.

Die folgende Tabelle zeigt beispielsweise, wie Residuen für 10 verschiedene Personen in der Studie berechnet werden:

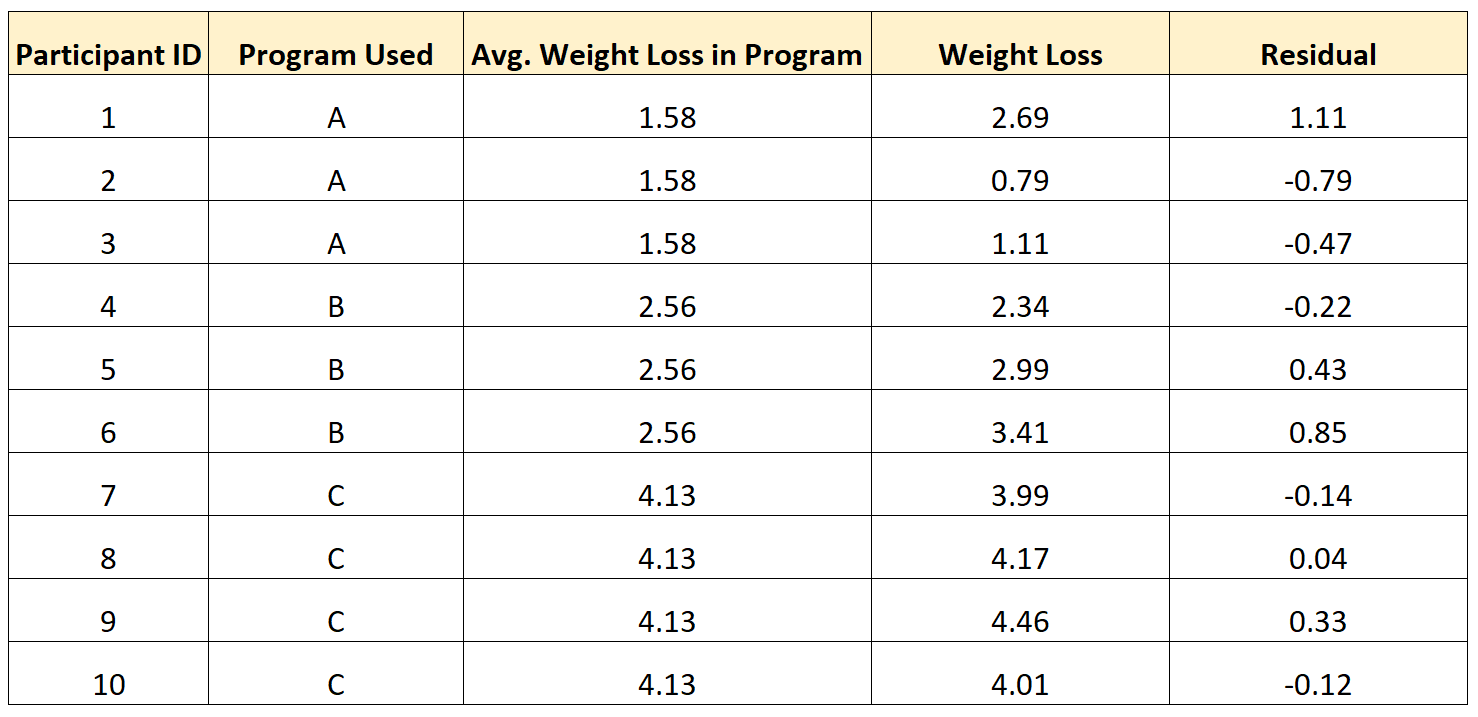
Beachten Sie das folgende Muster:

• Personen, deren Wert über ihrem Gruppendurchschnitt lag, hatten ein positives Residuum .
• Personen, deren Wert niedriger war als ihr Gruppenmittel, hatten ein negatives Residuum .

In der Praxis würden wir die Residuen für alle 90 Personen berechnen.

So verwenden Sie Residuen, um die Normalität zu überprüfen

Eine der Annahmen einer ANOVA ist, dass die Residuen normalverteilt sind.

Der gebräuchlichste Weg, diese Annahme zu überprüfen, ist die Erstellung eines QQ-Diagramms .

Wenn die Residuen normalverteilt sind, liegen die Punkte in einem QQ-Diagramm auf einer geraden diagonalen Linie.

So würde ein QQ-Diagramm für unser vorheriges Beispiel aussehen:

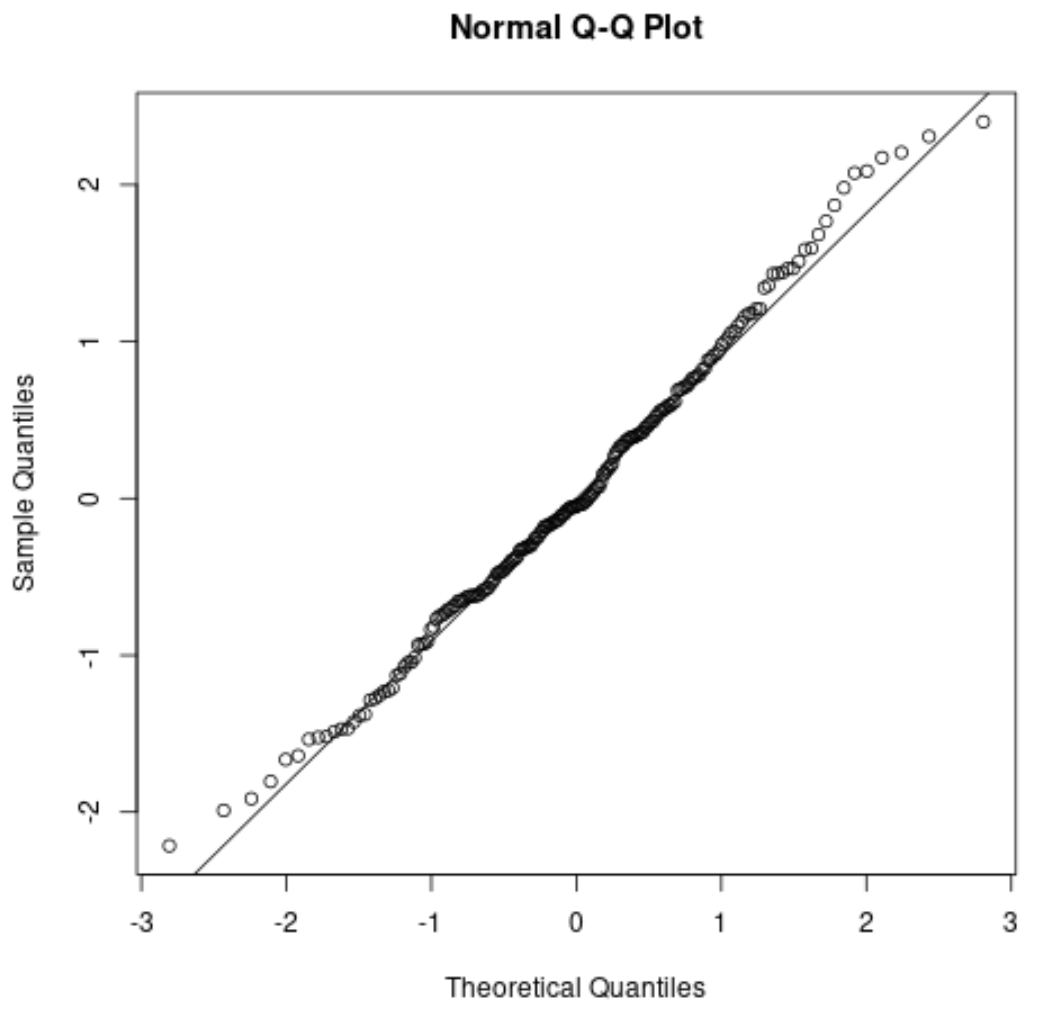
Die Spitzen weichen ein wenig von der geraden diagonalen Linie an den Enden des Schwanzes ab, aber im Allgemeinen folgen die Spitzen ganz gut der diagonalen Linie. Dies sagt uns, dass die Normalitätsannahme wahrscheinlich erfüllt ist.

Als Referenz sehen Sie hier, wie ein QQ-Diagramm für nicht normalverteilte Residuen aussehen könnte:

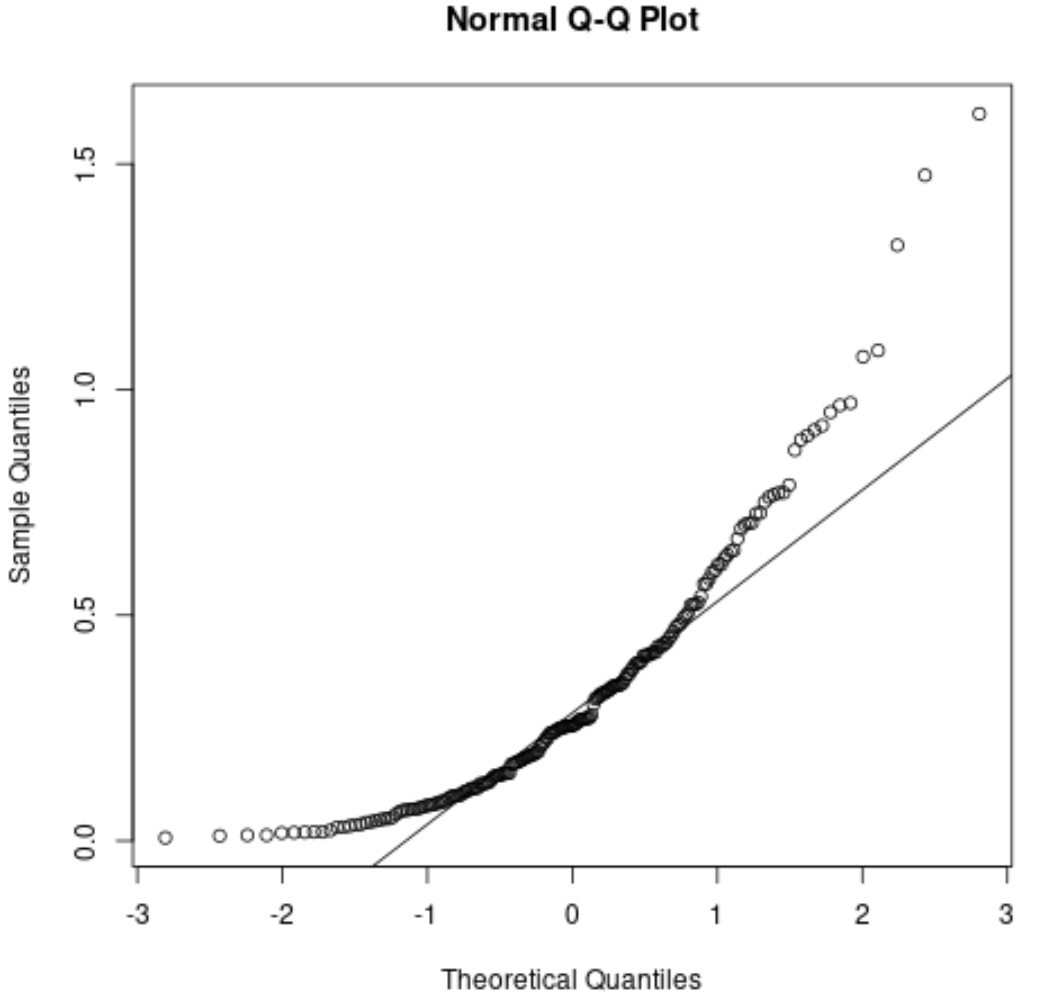
Die Punkte weichen stark von der geraden Diagonallinie ab, was darauf hindeutet, dass die Residuen nicht normalverteilt sind.

In den folgenden Tutorials erfahren Sie, wie Sie QQ-Diagramme in verschiedenen Softwareprogrammen erstellen:

• So erstellen Sie ein QQ-Diagramm in Excel
• So erstellen Sie ein QQ-Diagramm in R
• So erstellen Sie ein QQ-Diagramm in Python

Zusätzliche Ressourcen

Die folgenden Artikel bieten zusätzliche Informationen zu ANOVA-Modellen:

Eine Einführung in die einfaktorielle ANOVA
So überprüfen Sie ANOVA-Annahmen
4 Beispiele für die Verwendung von ANOVA im wirklichen Leben