So transformieren sie daten in python (log, quadratwurzel, kubikwurzel)

Viele statistische Tests gehen davon aus, dass Datensätze normalverteilt sind. Dies ist jedoch in der Praxis häufig nicht der Fall.

Eine Möglichkeit, dieses Problem zu lösen, besteht darin, die Werteverteilung in einem Datensatz mithilfe einer von drei Transformationen zu transformieren:

1. Log-Transformation: Transformieren Sie die Antwortvariable von y in log(y) .

2. Quadratwurzeltransformation: Transformieren Sie die Antwortvariable von y in √y .

3. Kubikwurzeltransformation: Transformieren Sie die Antwortvariable von y in y ^1/3 .

Durch die Durchführung dieser Transformationen wird der Datensatz im Allgemeinen normaler verteilt.

Die folgenden Beispiele zeigen, wie diese Transformationen in Python durchgeführt werden.

Protokolltransformation in Python

Der folgende Code zeigt, wie man eine logarithmische Transformation an einer Variablen durchführt und nebeneinander Diagramme erstellt, um die ursprüngliche Verteilung und die logarithmisch transformierte Verteilung der Daten anzuzeigen:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 4 , b= 15 , size= 300 )

#create log-transformed data
data_log = np. log (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Log-Transformed Data ')

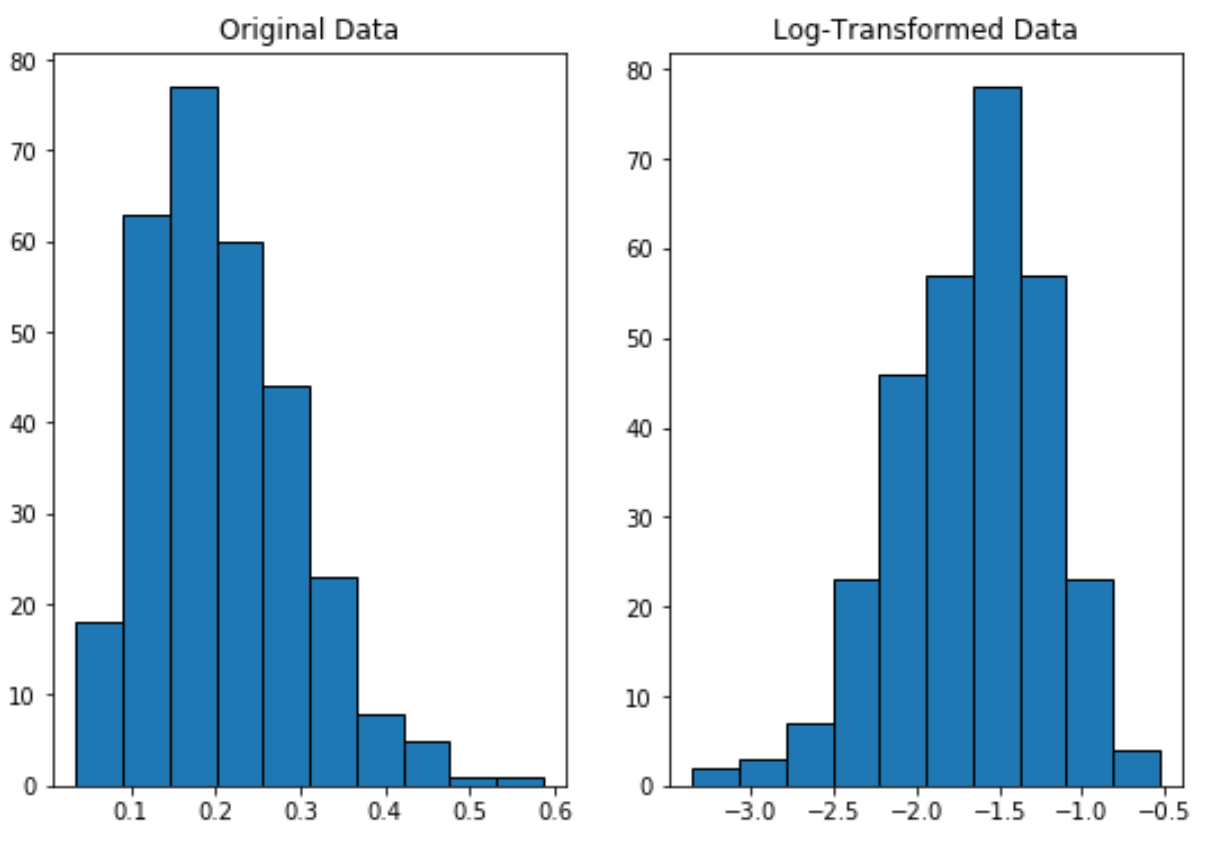
Beachten Sie, dass die logarithmisch transformierte Verteilung normaler verteilt ist als die Originalverteilung.

Es ist immer noch keine perfekte „Glockenform“, aber sie kommt einer Normalverteilung näher als der ursprünglichen Verteilung.

Quadratwurzeltransformation in Python

Der folgende Code zeigt, wie Sie eine Quadratwurzeltransformation für eine Variable durchführen und nebeneinander Diagramme erstellen, um die ursprüngliche Verteilung und die quadratwurzeltransformierte Verteilung der Daten anzuzeigen:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 1 , b= 5 , size= 300 )

#create log-transformed data
data_log = np. sqrt (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Square Root Transformed Data ') 

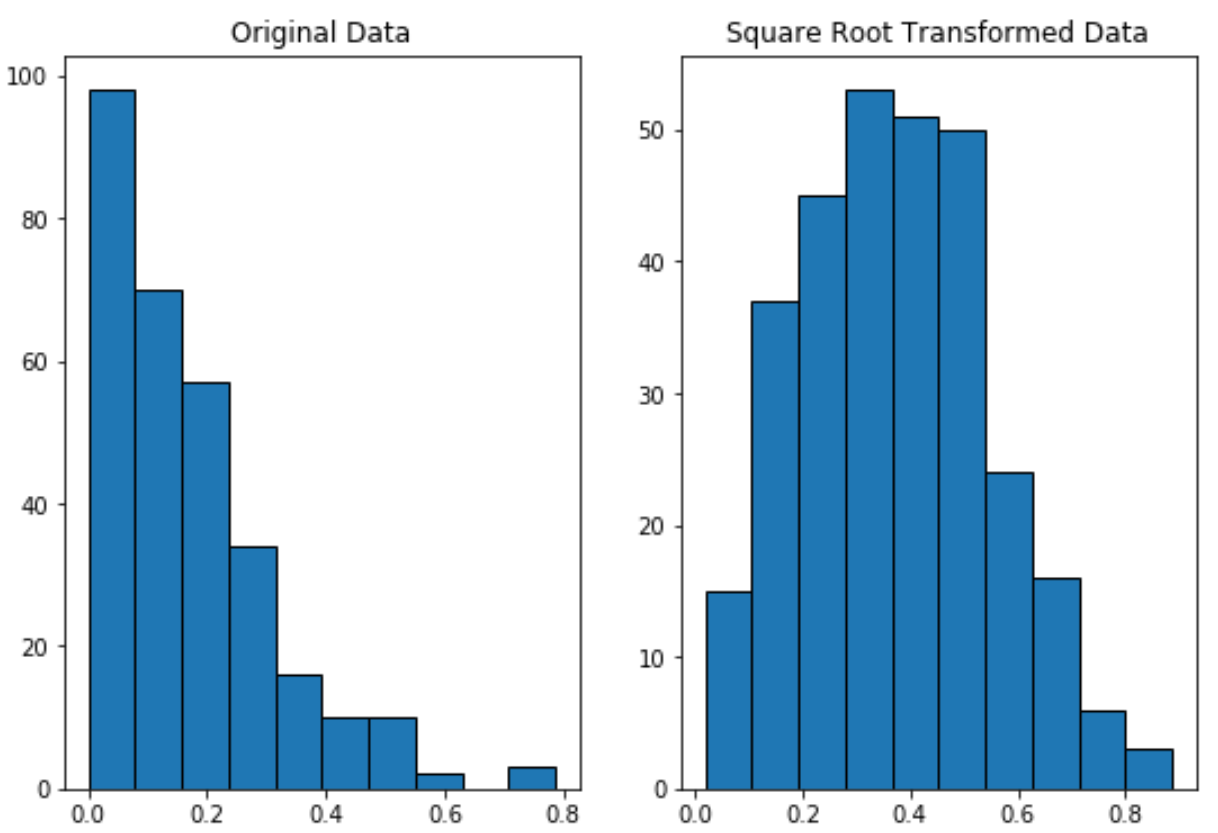
Beachten Sie, dass die Quadratwurzel-transformierten Daten viel normaler verteilt sind als die Originaldaten.

Würfelwurzeltransformation in Python

Der folgende Code zeigt, wie Sie eine Kubikwurzeltransformation für eine Variable durchführen und nebeneinander Diagramme erstellen, um die ursprüngliche Verteilung und die durch die Kubikwurzel transformierte Verteilung der Daten anzuzeigen:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (0)

#create beta distributed random variable with 200 values
data = np. random . beta (a= 1 , b= 5 , size= 300 )

#create log-transformed data
data_log = np. cbrt (data)

#define grid of plots
fig, axs = plt. subplots (nrows= 1 , ncols= 2 )

#create histograms
axs[0]. hist (data, edgecolor=' black ')
axs[1]. hist (data_log, edgecolor=' black ')

#add title to each histogram
axs[0]. set_title (' Original Data ')
axs[1].set_title(' Cube Root Transformed Data ') 

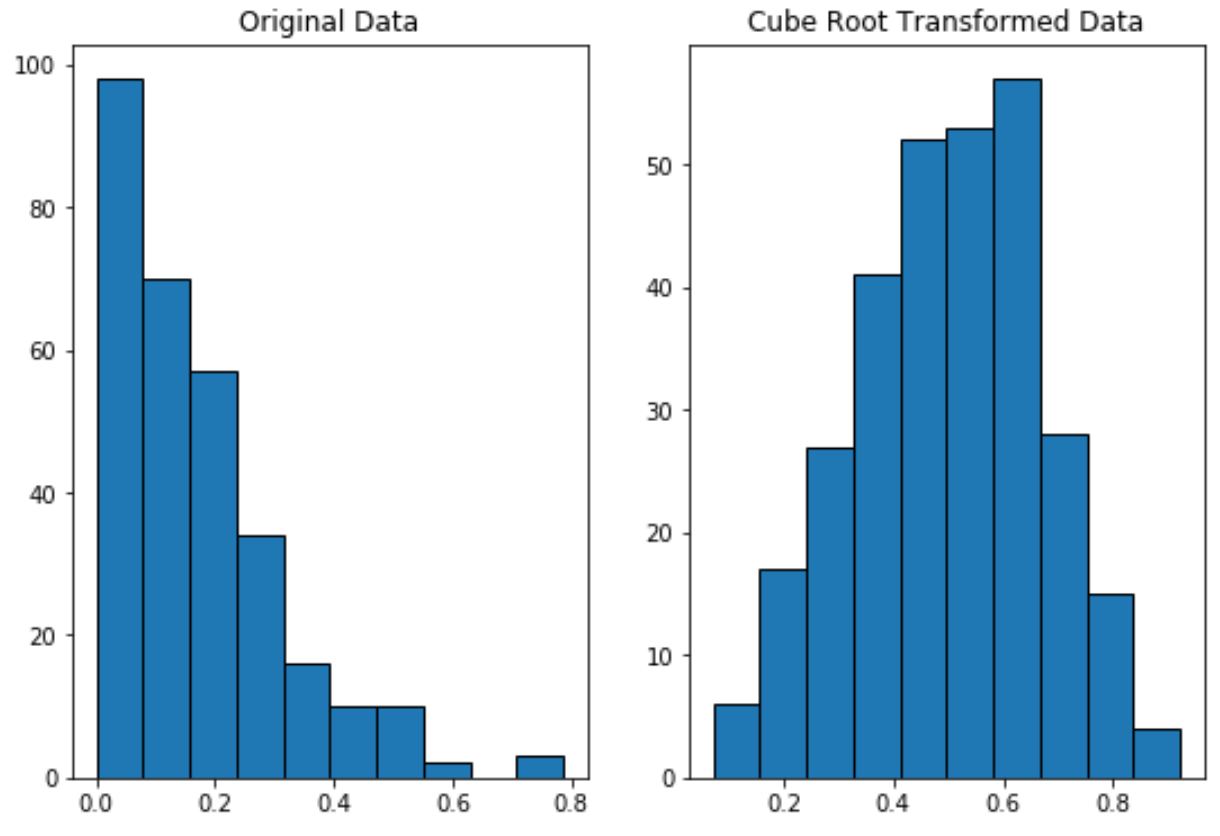
Beachten Sie, dass die durch die Kubikwurzel transformierten Daten viel normaler verteilt sind als die Originaldaten.

Zusätzliche Ressourcen

So berechnen Sie Z-Scores in Python
So normalisieren Sie Daten in Python
Was ist die Normalitätsannahme in der Statistik?