So transformieren sie daten in r (log, quadratwurzel, kubikwurzel)

Bei vielen statistischen Tests wird davon ausgegangen, dass die Residuen einer Antwortvariablen normalverteilt sind.

Allerdings sind die Residuen oft nicht normalverteilt. Eine Möglichkeit, dieses Problem zu lösen, besteht darin, die Antwortvariable mithilfe einer von drei Transformationen zu transformieren:

1. Log-Transformation: Transformieren Sie die Antwortvariable von y in log(y) .

2. Quadratwurzeltransformation: Transformieren Sie die Antwortvariable von y in √y .

3. Kubikwurzeltransformation: Transformieren Sie die Antwortvariable von y in y ^1/3 .

Durch die Durchführung dieser Transformationen nähert sich die Antwortvariable im Allgemeinen der Normalverteilung an. Die folgenden Beispiele zeigen, wie diese Transformationen in R durchgeführt werden.

Log-Transformation in R

Der folgende Code zeigt, wie eine Protokolltransformation für eine Antwortvariable durchgeführt wird:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

Der folgende Code zeigt, wie Histogramme erstellt werden, um die Verteilung von y vor und nach der Durchführung einer Protokolltransformation anzuzeigen:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

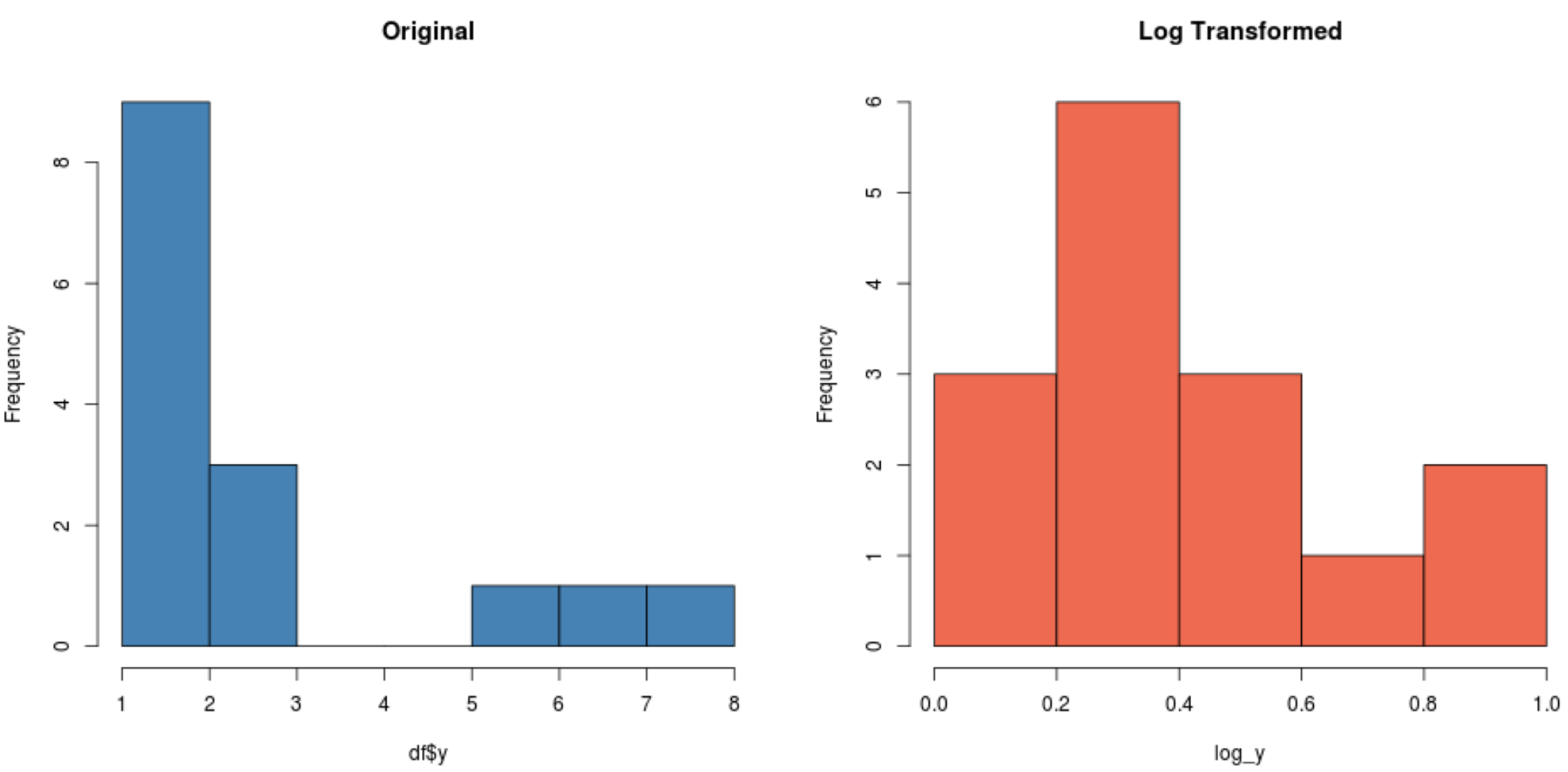
Beachten Sie, dass die logarithmisch transformierte Verteilung viel normaler ist als die ursprüngliche Verteilung. Es ist immer noch keine perfekte „Glockenform“, aber sie kommt einer Normalverteilung näher als der ursprünglichen Verteilung.

Wenn wir tatsächlich einen Shapiro-Wilk-Test für jede Verteilung durchführen, werden wir feststellen, dass die ursprüngliche Verteilung die Normalitätsannahme nicht erfüllt, während dies bei der logarithmisch transformierten Verteilung nicht der Fall ist (bei α = 0,05):

 #perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data: df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:log_y
W = 0.89089, p-value = 0.06917

Quadratwurzeltransformation in R

Der folgende Code zeigt, wie eine Quadratwurzeltransformation für eine Antwortvariable durchgeführt wird:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

Der folgende Code zeigt, wie Histogramme erstellt werden, um die Verteilung von y vor und nach der Durchführung einer Quadratwurzeltransformation anzuzeigen:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed') 

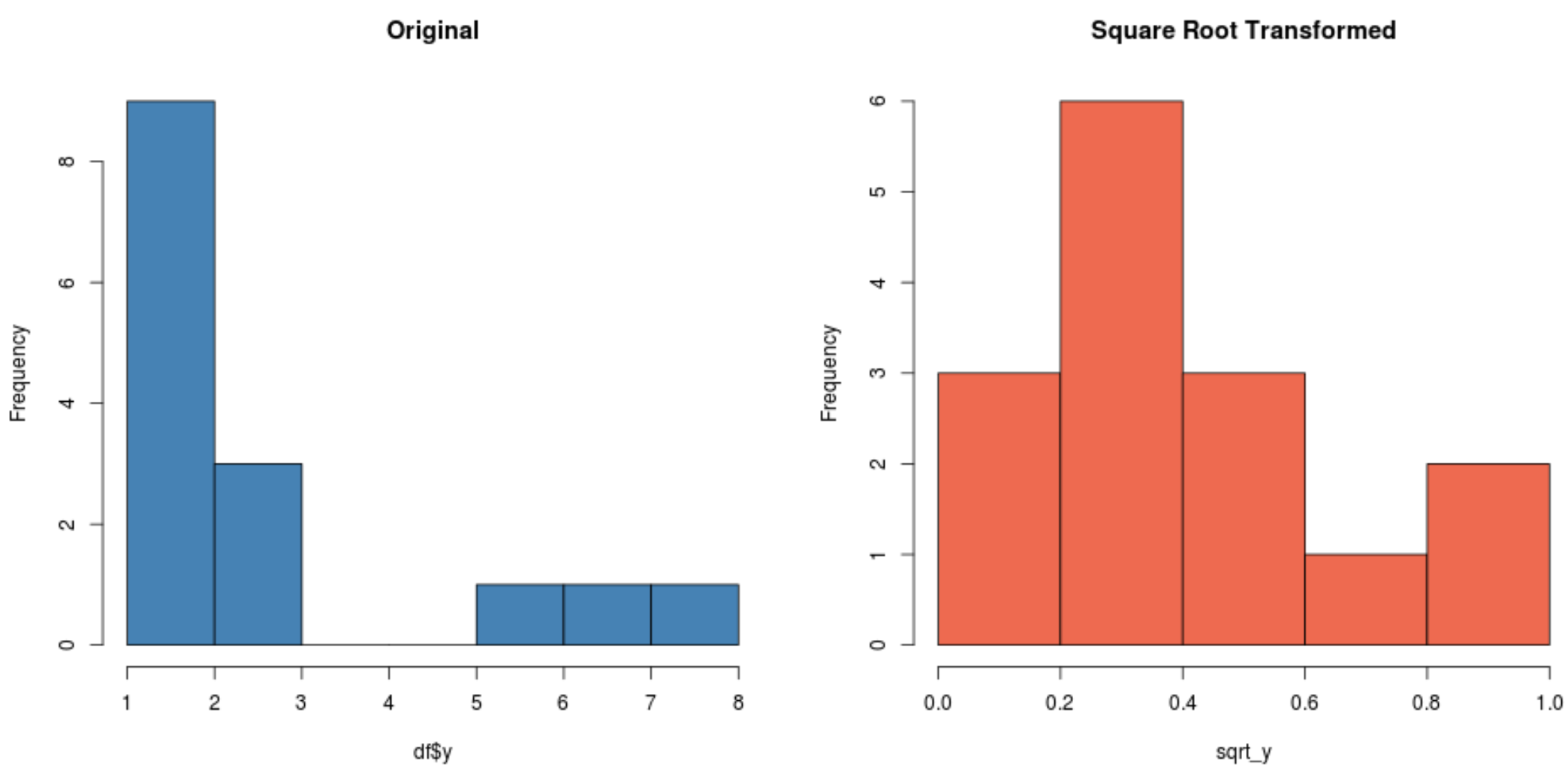
Beachten Sie, dass die Quadratwurzeltransformationsverteilung viel normaler verteilt ist als die Originalverteilung.

Kubikwurzeltransformation in R

Der folgende Code zeigt, wie eine Kubikwurzeltransformation für eine Antwortvariable durchgeführt wird:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

Der folgende Code zeigt, wie Histogramme erstellt werden, um die Verteilung von y vor und nach der Durchführung einer Quadratwurzeltransformation anzuzeigen:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed') 

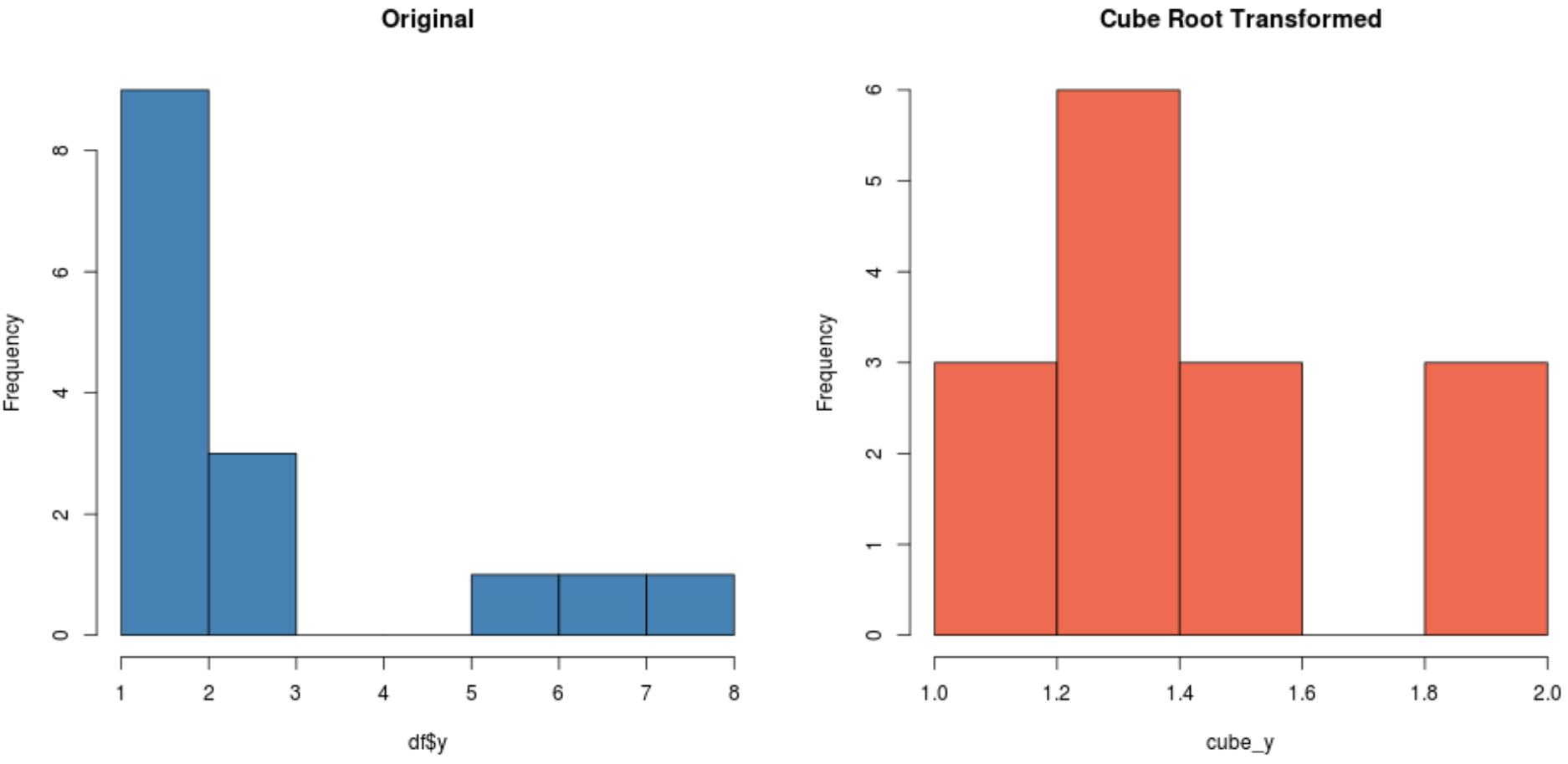
Abhängig von Ihrem Datensatz kann eine dieser Transformationen einen neuen Datensatz erzeugen, der normaler verteilt ist als die anderen.