Kovarianzmatrix

In diesem Artikel wird erläutert, was die Kovarianzmatrix ist und wie ihre Formel lautet. Anhand eines konkreten Beispiels erfahren Sie, wie Sie die Kovarianzmatrix erstellen und welche Eigenschaften Kovarianzmatrizen haben.

Was ist die Kovarianzmatrix?

Die Kovarianzmatrix ist eine quadratische Matrix, deren Elemente die Varianzen und Kovarianzen der untersuchten Variablen sind. Somit sind die Elemente der Hauptdiagonale der Kovarianzmatrix die Varianz jeder Variablen und die übrigen Elemente sind die Kovarianzen zwischen den Variablen.

In der Statistik wird die Kovarianzmatrix verwendet, um die Beziehung zwischen zwei oder mehr Zufallsvariablen zu analysieren. Die Kovarianzmatrix ist sehr nützlich, da Sie damit die Korrelation zwischen vielen Variablen schnell interpretieren können, da Sie die Werte aller Kovarianzen der Variablen gleichzeitig sehen können.

Das Symbol für die Kovarianzmatrix ist der griechische Großbuchstabe Sigma (Σ).

So berechnen Sie die Kovarianzmatrix

Um die Kovarianzmatrix mehrerer statistischer Variablen zu berechnen , müssen folgende Schritte durchgeführt werden:

1. Berechnen Sie die Varianzen aller Variablen.
2. Berechnen Sie die Kovarianz jedes Variablenpaares.
3. Bilden Sie die Kovarianzmatrix:
• Die Varianz der Variablen i muss auf der Hauptdiagonalen der Matrix platziert werden, genauer gesagt an der Position i,i .
• Die Kovarianz zwischen den Variablen i und j muss an der Position i,j der Matrix platziert werden.

Die Formel für die Kovarianzmatrix lautet daher wie folgt:

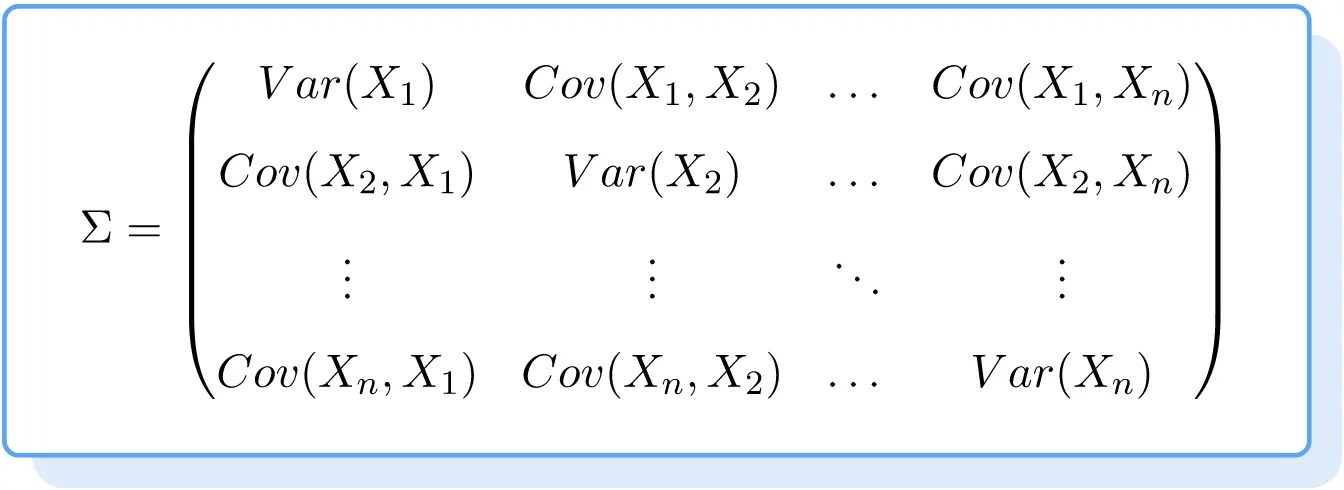
Beispiel einer Kovarianzmatrix

Nachdem Sie die Definition der Kovarianzmatrix gesehen haben, finden Sie unten eine Schritt-für-Schritt-Übung, damit Sie sehen können, wie diese Art von Matrix erstellt wird.

Berechnet die Kovarianzmatrix der Variablen X, Y und Z, deren Werte sind:

• X: 4, 7, 12, 5, 7
• Und: 9, 15, 19, 6, 8
• Z: 7, 2, 4, 6, 3

Als Erstes müssen wir die Varianzen aller Variablen bestimmen:

Zweitens ermitteln wir die Kovarianz zwischen jedem Variablenpaar:

Und nachdem wir alle Varianzen und Kovarianzen berechnet haben, müssen wir nur noch die Kovarianzmatrix erstellen. Dazu setzen wir die Varianzwerte auf die Hauptdiagonale der Matrix und die Kovarianzwerte an ihre entsprechende Position:

Wie Sie sehen, ist es durch die Darstellung der Varianzen und Kovarianzen in einer Matrix sehr einfach, die Variablen zu interpretieren. Die Variable mit der größten Streuung ist Y (23.44), andererseits haben die Variablen X und Y einen direkten Zusammenhang, während die Variablen X und Z (und damit Y und Z) einen umgekehrten Zusammenhang haben.

Beachten Sie, dass die Kovarianzmatrix immer symmetrisch ist, da die Kovarianz zwischen zwei Variablen nicht von der Reihenfolge der Variablen abhängt. Zum Beispiel,

ist gleich

Darüber hinaus ist die Kovarianzmatrix immer eine quadratische Matrix und ihre Dimension entspricht der Anzahl der Variablen. In diesem Fall hatten wir drei Variablen und deshalb ist es eine 3×3-Matrix, aber wenn wir nur zwei Variablen hätten, wäre die Kovarianzmatrix 2×2 gewesen.

Eigenschaften der Kovarianzmatrix

Die Kovarianzmatrix weist folgende Merkmale auf:

• Die Kovarianzmatrix ist eine quadratische Matrix in der Größenordnung der Anzahl der Variablen.
• Die Kovarianzmatrix ist symmetrisch, was bedeutet, dass die Hauptdiagonale der Matrix eine Symmetrieachse ist.
• Die Kovarianzmatrix ist immer positiv semidefinit.
• Die Determinante der Kovarianzmatrix ist gleich oder größer Null.