Dezile

In diesem Artikel erklären wir, was Dezile sind und wie sie berechnet werden. Sie finden auch mehrere gelöste, Schritt-für-Schritt-Beispiele für Dezilberechnungen und können darüber hinaus die Dezile jeder statistischen Stichprobe mit einem Online-Rechner berechnen.

Was sind Dezile?

In der Statistik sind Dezile die neun Werte, die einen Satz geordneter Daten in zehn gleiche Teile unterteilen. Das erste, zweite, dritte, … Dezil repräsentiert also 10 %, 20 %, 30 %, … der Stichprobe oder Grundgesamtheit.

Beispielsweise ist der Wert des vierten Dezils höher als 40 % der Daten, aber niedriger als der Rest der Daten.

Dezile werden durch den Großbuchstaben D und den Dezilindex dargestellt, d. h. das erste Dezil ist D ₁ , das zweite Dezil ist D ₂ , das dritte Dezil ist D ₃ usw.

👉 Mit dem Rechner unten können Sie Dezile für jeden Datensatz berechnen.

Es ist zu beachten, dass Dezile ebenso wie Quartile, Quintile und Perzentile ein Maß für die nichtzentrale Position sind. Sie können die Bedeutung jedes dieser Quantiltypen auf unserer Website überprüfen.

Darüber hinaus entspricht das fünfte Dezil dem Median und dem zweiten Quartil, da sie den gesamten Datensatz in zwei gleiche Teile teilen.

So berechnen Sie Dezile

Um die Dezilposition einer Reihe statistischer Daten zu berechnen , multiplizieren Sie die Dezilzahl mit der Summe der Gesamtzahl der Daten plus eins und dividieren Sie das Ergebnis durch zehn.

Die Dezilformel lautet daher:

Bitte beachten Sie: Diese Formel sagt uns die Position des Dezils, nicht den Wert des Dezils. Das Dezil sind die Daten, die sich an der durch die Formel ermittelten Position befinden.

Manchmal liefert uns das Ergebnis dieser Formel jedoch eine Dezimalzahl. Daher müssen wir zwei Fälle unterscheiden, je nachdem, ob das Ergebnis eine Dezimalzahl ist oder nicht:

• Wenn das Ergebnis der Formel eine Zahl ohne Dezimalteil ist, sind das Dezil die Daten, die sich an der durch die obige Formel angegebenen Position befinden.
• Wenn das Ergebnis der Formel eine Zahl mit Dezimalteil ist, wird der Dezilwert nach folgender Formel berechnet:

Dabei sind x _i und x _i+1 die Zahlen der Positionen, zwischen denen sich die durch die erste Formel erhaltene Zahl befindet, und d ist der Dezimalteil der durch die erste Formel erhaltenen Zahl.

Nun denken Sie vielleicht, dass es komplex ist, die Dezile einer statistischen Stichprobe zu ermitteln, aber in der Praxis ist es ganz einfach. Wenn Sie die folgenden beiden Beispiele lesen, werden Sie es sicherlich viel besser verstehen.

Hinweis : Die wissenschaftliche Gemeinschaft ist sich nicht ganz einig, wie man Dezile berechnet, daher gibt es Statistikbücher, die es etwas anders erklären.

Beispiel einer Dezilberechnung

Wie Sie oben gesehen haben, hängt die Berechnung von Dezilen davon ab, ob die Zahl, die uns die erste Formel liefert, dezimal ist oder nicht. Deshalb haben wir unten zwei gelöste Beispiele vorbereitet, eines für jeden Fall. Denken Sie auf jeden Fall daran, dass Sie Fragen zur Zusammensetzung der Dezile in den Kommentaren stellen können.

Beispiel 1

• Ermitteln Sie anhand der folgenden Daten, vom kleinsten zum größten, das erste, dritte und achte Dezil der Stichprobe.

Die Daten in dieser Übung sind bereits sortiert, sodass die Reihenfolge nicht geändert werden muss, andernfalls müssten wir die Daten zuerst vom kleinsten zum größten sortieren.

Wie oben erläutert, lautet die Formel, die es ermöglicht, die Positionen der Dezile zu ermitteln, wie folgt:

Die Stichprobengröße für diese Übung beträgt 29 Beobachtungen. Um die Position des ersten Dezils zu berechnen, müssen Sie also 29 für n und 1 für k ersetzen:

Das Ergebnis der Formel ist 3, sodass das erste Dezil an dritter Stelle der geordneten Liste steht und dieser Wert 85 entspricht.

Jetzt wenden wir das gleiche Verfahren noch einmal an, jedoch mit dem dritten Dezil. Wir verwenden die Formel, indem wir das k durch eine 3 ersetzen:

Das dritte Dezil wird daher das Element an neunter Stelle sein, also 97.

Schließlich führen wir den gleichen Vorgang durch, fügen jedoch eine 8 in die Formel ein, um das achte Dezil zu bestimmen:

Das achte Dezil ist die Zahl an Position 24 der geordneten Datenliste, das achte Dezil ist also 131.

Beispiel 2

• Berechnen Sie anhand der Daten in der folgenden Tabelle die Dezile 4, 7 und 9.

Um die Positionen der Dezile zu ermitteln, müssen Sie wie im vorherigen Beispiel die folgende Formel verwenden:

In diesem Fall beträgt die Stichprobengröße 42. Um die Position des vierten Dezils zu ermitteln, müssen Sie den Parameter n durch 42 und k durch 4 ersetzen:

Aber dieses Mal haben wir aus der Formel eine Dezimalzahl erhalten, also müssen wir die folgende Formel anwenden, um das genaue Dezil zu berechnen:

Die aus der ersten Formel erhaltene Zahl ist 17,2, das vierte Dezil liegt also zwischen dem siebzehnten und dem achtzehnten gegebenen Dezil, also 109 bzw. 112. Daher ist x _i 109, x _{i+ 1} ist 112 und d ist der Dezimalteil. der erhaltenen Zahl, also 0,2.

Wir wiederholen den gleichen Vorgang, um das siebte Dezil zu finden. Wir berechnen zunächst die Position des Dezils:

Aus der Formel haben wir die Zahl 30,1 erhalten, was bedeutet, dass das Dezil zwischen den Positionen 30 und 31 liegt, deren Werte 154 und 159 sind. Die Berechnung des genauen Dezils lautet daher:

Abschließend wenden wir die gleiche Methode noch einmal an, um das neunte Dezil zu erhalten. Wir bestimmen die Position des Dezils:

Die erhaltene Zahl ist dezimal und liegt zwischen 38 und 39, deren Positionen den Werten 189 und 196 entsprechen. Somit lautet die Berechnung von Dezil 9:

Dezilrechner

Geben Sie einen statistischen Datensatz in den Rechner unten ein, um Dezile zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Dezile in gruppierten Daten

Um Dezile zu berechnen, wenn Daten in Intervalle gruppiert werden , müssen wir zunächst mithilfe der folgenden Formel das Intervall oder die Klasse ermitteln, in die das Dezil fällt:

Das Dezil liegt daher in dem Intervall, dessen absolute Häufigkeit unmittelbar größer ist als die im vorherigen Ausdruck erhaltene Zahl.

Und sobald wir bereits wissen, zu welchem Intervall das Dezil gehört, müssen wir die folgende Formel anwenden, um den genauen Wert des Dezils zu ermitteln:

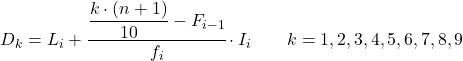
Gold:

• L _i ist die untere Grenze des Intervalls, in dem sich das Dezil befindet.
• n ist die Gesamtzahl der statistischen Daten.
• F _i-1 ist die kumulative absolute Häufigkeit des vorherigen Intervalls.
• f _i ist die absolute Häufigkeit des Intervalls, in dem sich das Dezil befindet.
• I _i ist die Breite des Dezilintervalls.

Damit Sie sehen können, wie das geht, haben Sie unten eine abgeschlossene Übung, in der die Dezile 3, 5 und 8 der folgenden nach Intervallen gruppierten Daten berechnet werden.

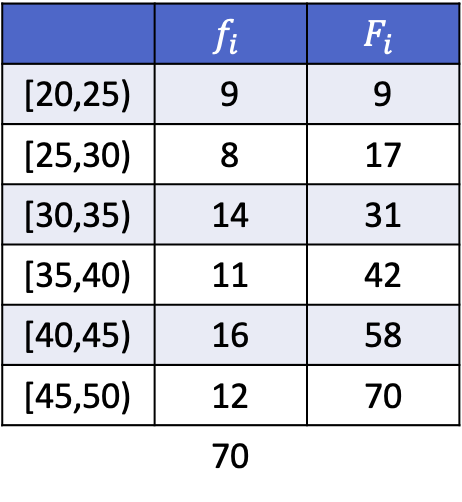
Da die Daten gruppiert sind, besteht die Berechnung jedes Dezils aus zwei Schritten: Zuerst wird das Intervall ermittelt, in das das Dezil fällt, und dann wird der genaue Wert des Dezils berechnet. Wir finden daher das Intervall des dritten Dezils:

Das Dezilintervall ist dasjenige, dessen absolute kumulative Häufigkeit unmittelbar größer als 21,3 ist, und in diesem Fall ist es das Intervall [30,35), dessen absolute kumulative Häufigkeit 31 beträgt. Da wir nun das Dezilintervall kennen, wenden wir zur Ermittlung die folgende Formel an der genaue Wert des Dezils:

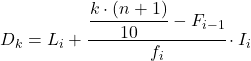
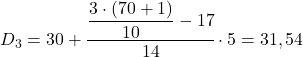
Wir müssen die Methode nun erneut anwenden, um das fünfte Dezil zu erhalten. Wir bestimmen zunächst das Intervall, in dem es liegt:

Das Ergebnis 35 bedeutet, dass es im Intervall [35,40) liegt, aber nicht, weil es eine 35 im Intervallausdruck gibt, sondern weil seine akkumulierte absolute Häufigkeit (42) am unmittelbarsten am höchsten ist. Und sobald das Intervall identifiziert ist, wenden wir die zweite Formel des Prozesses an:

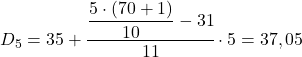
Schließlich finden wir das achte Dezil. Dazu berechnen wir zunächst sein Intervall:

Die kumulative absolute Häufigkeit unmittelbar über 56,8 beträgt 58, der achte Dezilbereich beträgt also [40,45]. Es reicht daher aus, den genauen Wert des Dezils zu bestimmen: