So berechnen sie dfbetas in r

In der Statistik wollen wir oft wissen, welchen Einfluss verschiedene Beobachtungen auf Regressionsmodelle haben.

Eine Möglichkeit, den Einfluss von Beobachtungen zu berechnen, ist die Verwendung einer Metrik namens DFBETAS , die uns den standardisierten Effekt auf jeden Koeffizienten beim Entfernen jeder einzelnen Beobachtung angibt.

Diese Metrik gibt uns eine Vorstellung vom Einfluss jeder Beobachtung auf jede Koeffizientenschätzung in einem bestimmten Regressionsmodell.

Dieses Tutorial zeigt ein Schritt-für-Schritt-Beispiel für die Berechnung und Visualisierung von DFBETAS für jede Beobachtung in einem Modell in R.

Schritt 1: Erstellen Sie ein Regressionsmodell

Zuerst erstellen wir ein multiples lineares Regressionsmodell unter Verwendung des in R integrierten mtcars- Datensatzes:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Schritt 2: Berechnen Sie DFBETAS für jede Beobachtung

Als Nächstes verwenden wir die integrierte Funktion dfbetas() , um die DFBETAS-Werte für jede Beobachtung im Modell zu berechnen:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

Für jede Beobachtung können wir den Unterschied in der Koeffizientenschätzung für den Ursprung, die Variable disp und die Variable hp sehen, der auftritt, wenn wir diese bestimmte Beobachtung entfernen.

Im Allgemeinen gehen wir davon aus, dass eine Beobachtung einen starken Einfluss auf die Schätzung eines bestimmten Koeffizienten hat, wenn ihr DBETAS-Wert größer als ein Schwellenwert von 2/√ n ist, wobei n die Anzahl der Beobachtungen ist.

In diesem Beispiel wäre der Schwellenwert 0,3535534 :

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

Schritt 3: Visualisieren Sie die DFBETAS

Schließlich können wir Diagramme erstellen, um den DFBETAS-Wert für jede Beobachtung und jeden Prädiktor im Modell zu visualisieren:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

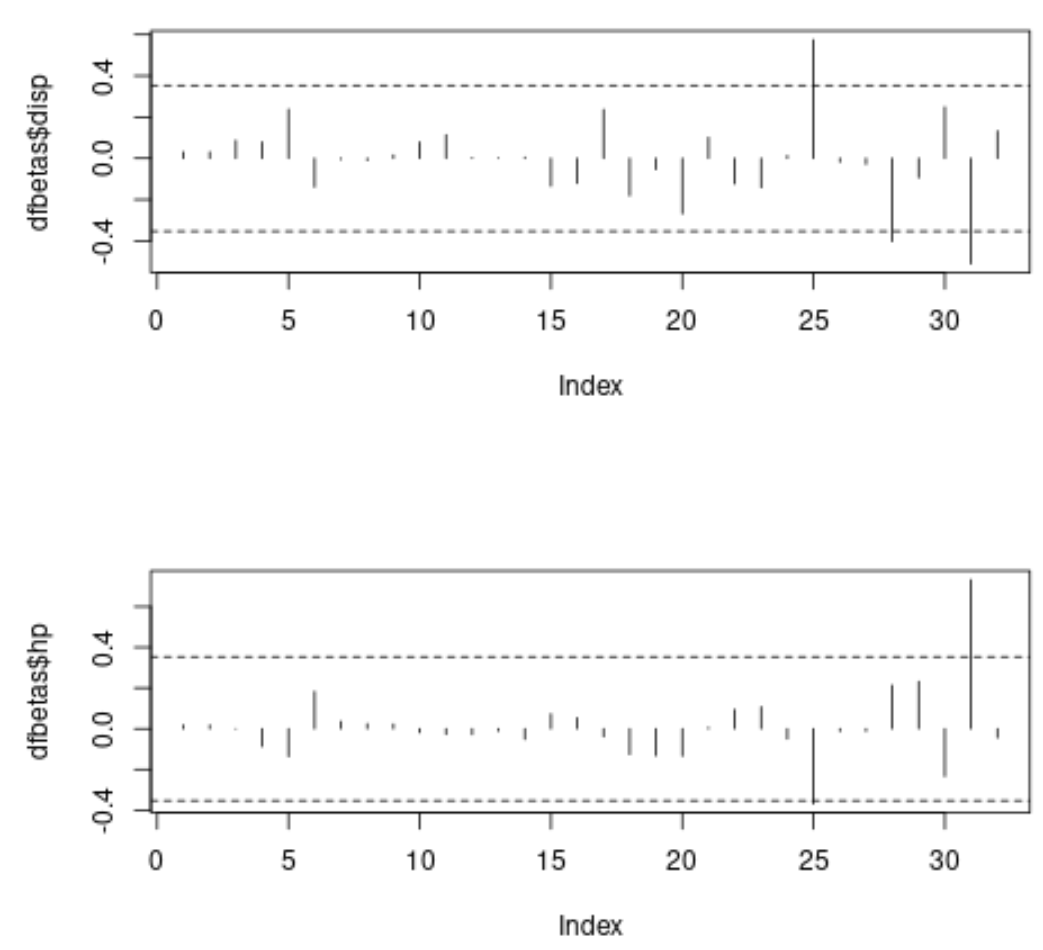
In jedem Diagramm zeigt die x-Achse den Index jeder Beobachtung im Datensatz an und der y-Wert zeigt die entsprechenden DFBETAS für jede Beobachtung und jeden Prädiktor an.

Im ersten Diagramm können wir sehen, dass drei Beobachtungen den absoluten Schwellenwert von 0,3535534 überschreiten, und im zweiten Diagramm können wir sehen, dass zwei Beobachtungen den absoluten Schwellenwert überschreiten.

Möglicherweise entscheiden wir uns dafür, diese Beobachtungen genauer zu untersuchen, um festzustellen, ob sie einen übermäßigen Einfluss auf die Schätzung der Modellkoeffizienten haben.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So berechnen Sie Hebelstatistiken in R
So berechnen Sie DFFITS in R