So interpretieren sie diagnosediagramme in r

Lineare Regressionsmodelle werden verwendet, um die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen zu beschreiben.

Sobald wir jedoch ein Regressionsmodell angepasst haben, empfiehlt es sich, auch Diagnosediagramme zu erstellen, um die Modellresiduen zu analysieren und sicherzustellen, dass ein lineares Modell für die jeweiligen Daten, mit denen wir arbeiten, geeignet ist.

In diesem Tutorial wird erläutert, wie Diagnosediagramme für ein bestimmtes Regressionsmodell in R erstellt und interpretiert werden.

Beispiel: Diagnosediagramme in R erstellen und interpretieren

Angenommen, wir passen ein einfaches lineares Regressionsmodell unter Verwendung von „Studienstunden“ an, um die „Prüfungsnote“ von Schülern in einer bestimmten Klasse vorherzusagen:

 #create data frame
df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

Mit dem Befehl plot() können wir vier Diagnosediagramme für dieses Regressionsmodell erstellen:

 #produce diagnostic plots for regression model
plot(model)

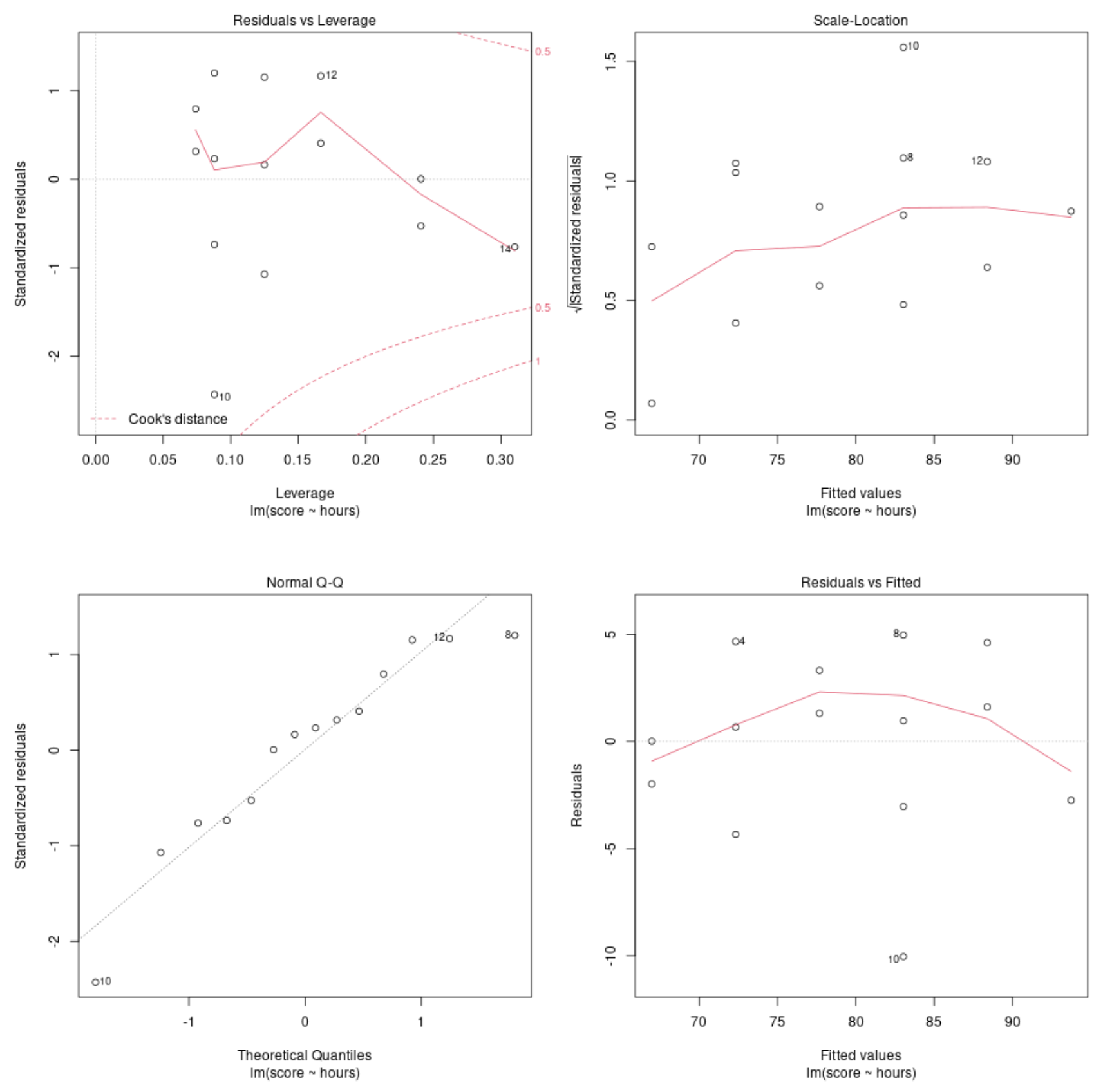
Diagnosetabelle Nr. 1: Restwerte vs. Leverage-Diagramm

Dieses Diagramm wird verwendet, um einflussreiche Beobachtungen zu identifizieren. Wenn Punkte in diesem Diagramm außerhalb der Cook-Distanz (gepunktete Linien) liegen, handelt es sich um eine einflussreiche Beobachtung.

In unserem Beispiel können wir sehen, dass Beobachtung Nr. 10 der Cook-Distanzgrenze am nächsten kommt, aber nicht außerhalb der gepunkteten Linie liegt. Dies bedeutet, dass es in unserem Datensatz keine übermäßig einflussreichen Punkte gibt.

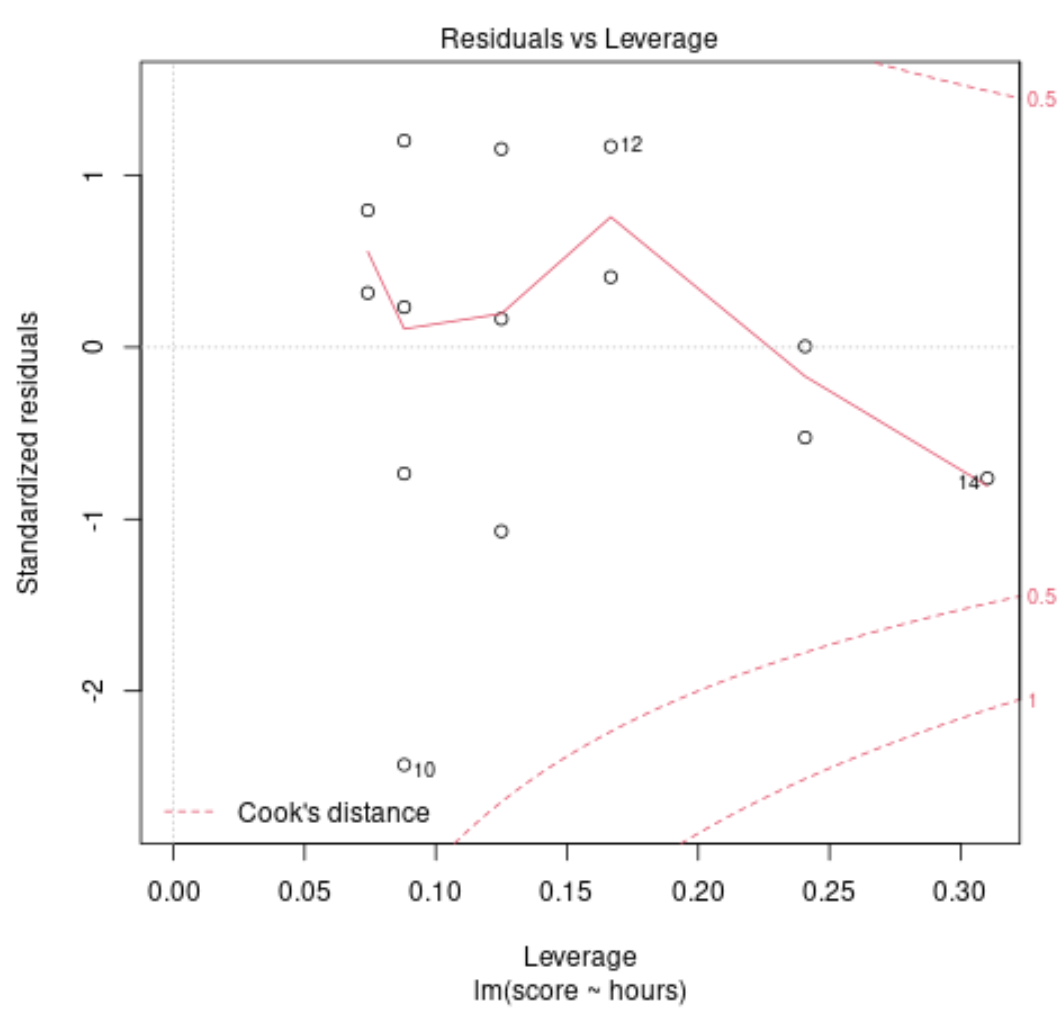
Diagnosediagramm Nr. 2: Maßstabs- und Standortdiagramm

Dieses Diagramm wird verwendet, um die Annahme der Varianzgleichheit (auch „Homoskedastizität“ genannt) zwischen den Residuen unseres Regressionsmodells zu überprüfen. Wenn die rote Linie im Diagramm ungefähr horizontal verläuft, ist die Annahme gleicher Varianz wahrscheinlich erfüllt.

In unserem Beispiel können wir sehen, dass die rote Linie im Diagramm nicht genau horizontal verläuft, aber an keiner Stelle zu stark abweicht. Wir stellen wahrscheinlich fest, dass die Annahme gleicher Varianz in diesem Fall nicht verletzt wird.

Verwandte Themen: Heteroskedastizität in der Regressionsanalyse verstehen

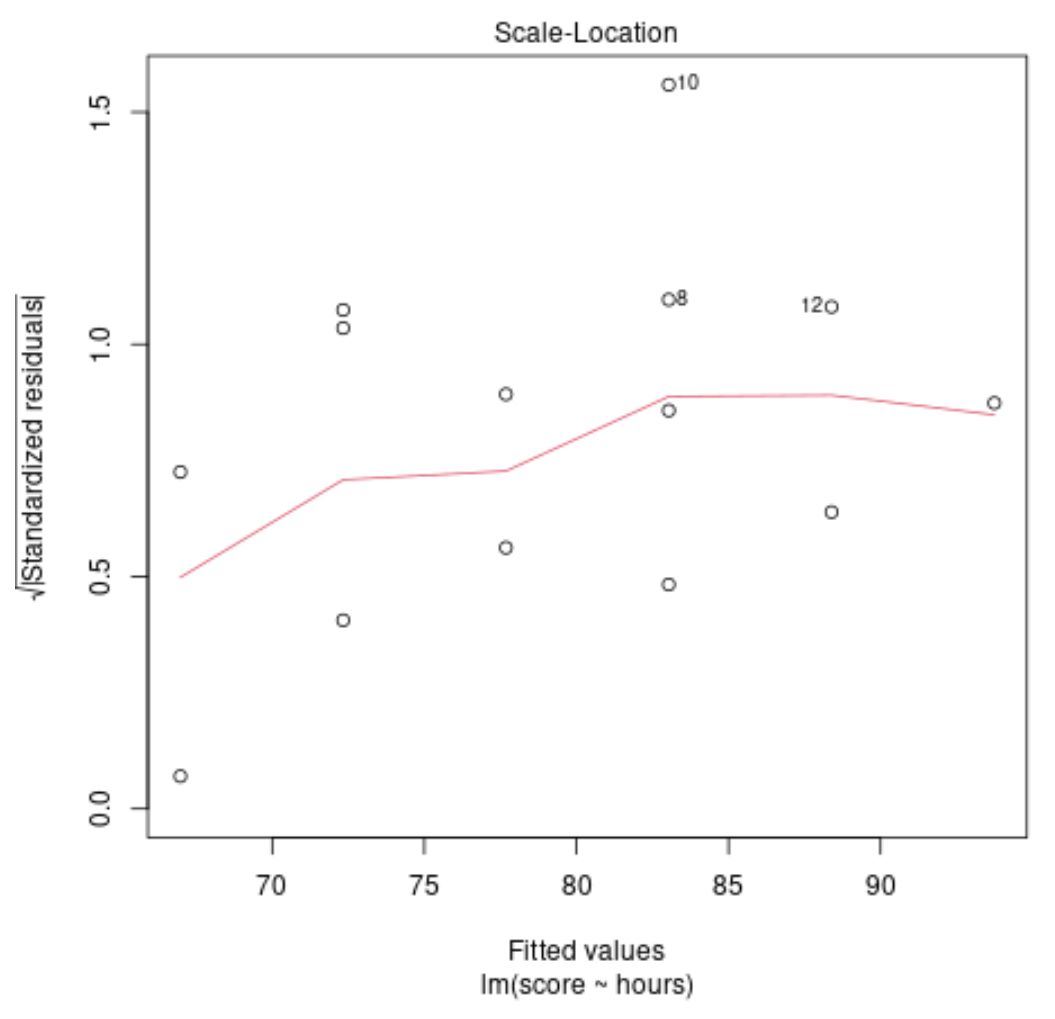
Diagnose-Trace Nr. 3: normale QQ-Trace

Dieses Diagramm wird verwendet, um zu bestimmen, ob die Residuen aus dem Regressionsmodell normalverteilt sind. Wenn die Punkte in diesem Diagramm ungefähr entlang einer geraden diagonalen Linie liegen, können wir davon ausgehen, dass die Residuen normalverteilt sind.

In unserem Beispiel können wir sehen, dass die Punkte ungefähr entlang der diagonalen Geraden liegen. Die Beobachtungen Nr. 10 und Nr. 8 weichen ein wenig von der Linie an den Enden ab, aber nicht genug, um zu erklären, dass die Residuen nicht normalverteilt sind.

Diagnosediagramm Nr. 4: Residuen vs. Angepasste Handlung

Dieses Diagramm wird verwendet, um zu bestimmen, ob die Residuen nichtlineare Muster aufweisen. Wenn die rote Linie in der Mitte des Diagramms ungefähr horizontal verläuft, können wir davon ausgehen, dass die Residuen einem linearen Muster folgen.

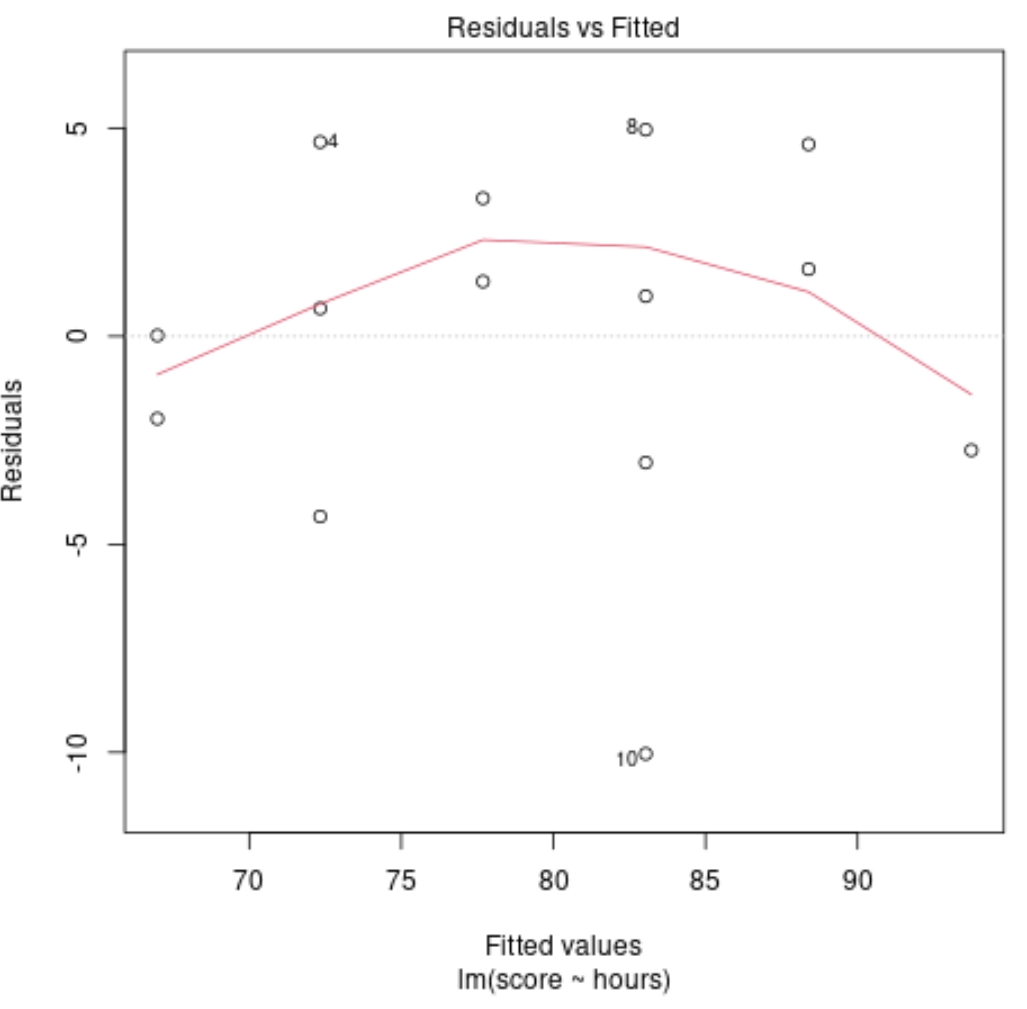
In unserem Beispiel können wir sehen, dass die rote Linie von einer perfekten horizontalen Linie abweicht, jedoch nicht wesentlich. Wir geben wahrscheinlich an, dass die Residuen einem ungefähr linearen Muster folgen und dass ein lineares Regressionsmodell für diesen Datensatz geeignet ist.

Zusätzliche Ressourcen

Die vier Annahmen der linearen Regression
Was sind Residuen in der Statistik?
So erstellen Sie ein Residuendiagramm in R
So interpretieren Sie ein Maßstabs- und Standortdiagramm