Dichtefunktion
In diesem Artikel erfahren Sie, was die Dichtefunktion ist, wie aus der Dichtefunktion eine Wahrscheinlichkeit berechnet wird und welche Eigenschaften diese Wahrscheinlichkeitsfunktion hat. Darüber hinaus können Sie die Unterschiede zwischen der Dichtefunktion und der Verteilungsfunktion erkennen.
Was ist die Dichtefunktion?
Die Dichtefunktion , auch Wahrscheinlichkeitsdichtefunktion genannt, ist eine mathematische Funktion, die die Wahrscheinlichkeit beschreibt, dass eine kontinuierliche Zufallsvariable einen bestimmten Wert annimmt.
Mit anderen Worten: Die einer Variablen zugeordnete Dichtefunktion definiert mathematisch die Wahrscheinlichkeiten, mit denen die Variable einen Wert annimmt.
Nehmen wir beispielsweise an, dass die Wahrscheinlichkeit, dass ein Erwachsener in einer Bevölkerung größer als 1,80 m ist, 35 % beträgt, dann wird die Dichtefunktion bei der Berechnung dieser Wahrscheinlichkeit eine Wahrscheinlichkeit von 35 % angeben.
Manchmal wird die Wahrscheinlichkeitsdichtefunktion als PDF abgekürzt.
Berechnen Sie eine Wahrscheinlichkeit mit der Dichtefunktion
Um die Wahrscheinlichkeit zu ermitteln, dass eine kontinuierliche Variable einen Wert in einem Intervall annimmt, muss das Integral der Dichtefunktion berechnet werden, die dieser Variablen zwischen den Grenzen des Intervalls zugeordnet ist.
![]()
Gold
![]()
ist die Dichtefunktion der kontinuierlichen Zufallsvariablen.
Mit anderen Worten: Die Wahrscheinlichkeit, dass die Variable in einem Intervall einen Wert annimmt, entspricht der Fläche unter der Dichtefunktion in diesem Intervall.
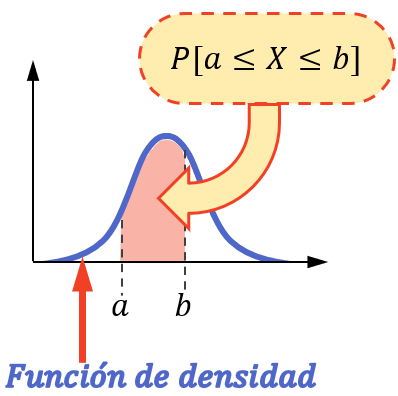
Beachten Sie, dass die Wahrscheinlichkeitsberechnung nur auf diese Weise durchgeführt werden kann, wenn die statistische Variable einer kontinuierlichen Verteilung folgt, beispielsweise einer Normalverteilung, einer Exponentialverteilung, einer Poisson-Verteilung usw.
Eigenschaften der Dichtefunktion
Die Dichtefunktion hat folgende Eigenschaften:
- Der Wert der Dichtefunktion ist für jeden Wert von x Null oder positiv.
![]()
- Darüber hinaus ist der Maximalwert der Dichtefunktion gleich 1.
![]()
- Tatsächlich ist die Gesamtfläche unter dem Dichtefunktionsgraphen unabhängig von der Variablen immer äquivalent zu 1, da sie der Menge aller Wahrscheinlichkeiten entspricht.
![]()
- Wie im vorherigen Abschnitt erläutert, wird die Wahrscheinlichkeit, dass eine kontinuierliche Variable in einem Intervall einen Wert annimmt, mit dem Integral der Dichtefunktion in diesem Intervall berechnet.
![]()
Dichtefunktion und Verteilungsfunktion
In diesem letzten Abschnitt werden wir sehen, wie sich die Dichtefunktion und die Verteilungsfunktion unterscheiden, da es sich um zwei Arten von Wahrscheinlichkeitsfunktionen handelt, die im Allgemeinen verwechselt werden.
Mathematisch entspricht die Verteilungsfunktion dem Integral der Dichtefunktion , sodass die Verteilungsfunktion die kumulative Wahrscheinlichkeit einer kontinuierlichen Variablen beschreibt.
Das heißt, das Bild der Verteilungsfunktion für jeden Wert ist gleich der Wahrscheinlichkeit, dass die Variable diesen Wert oder einen niedrigeren Wert annimmt.
Die mathematische Beziehung zwischen diesen beiden Arten von Funktionen ist daher wie folgt:
![]()
Gold
![]()
ist die Dichtefunktion und
![]()
ist die Verteilungsfunktion.
Beachten Sie, wie sich die grafische Darstellung der Dichtefunktion relativ zu ihrer Verteilungsfunktion einer Variablen ändert, die einer Normalverteilung mit einem Mittelwert von 1 und einer Standardabweichung von 0,5 folgt:

Um mehr über die Verteilungsfunktion zu erfahren, klicken Sie auf den folgenden Link: