Was sind dichtekurven? (erklärung & beispiele)

Eine Dichtekurve ist eine Kurve in einem Diagramm, die die Werteverteilung in einem Datensatz darstellt. Dies ist aus drei Gründen nützlich:

1. Eine Dichtekurve gibt uns eine gute Vorstellung von der „Form“ einer Verteilung, einschließlich der Frage, ob eine Verteilung einen oder mehrere „Spitzen“ von Häufigkeitswerten aufweist und ob die Verteilung nach links schief ist oder nicht oder richtig. RECHTS. .

2. Eine Dichtekurve ermöglicht es uns, visuell zu sehen, in welcher Beziehung der Mittelwert und der Median einer Verteilung stehen.

3. Mithilfe einer Dichtekurve können wir visuell sehen, wie viel Prozent der Beobachtungen in einem Datensatz zwischen verschiedenen Werten liegen.

Die bekannteste Dichtekurve ist die Glockenkurve, die dieNormalverteilung darstellt.

Um Dichtekurven besser zu verstehen, betrachten Sie das folgende Beispiel.

Beispiel: Erstellen und Interpretieren einer Dichtekurve

Nehmen wir an, wir haben den folgenden Datensatz, der die Höhe von 20 verschiedenen Pflanzen (in Zoll) in einem bestimmten Feld zeigt:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

Wenn wir ein einfaches Histogramm erstellen würden, um die relativen Häufigkeiten jedes Werts anzuzeigen, würde es so aussehen:

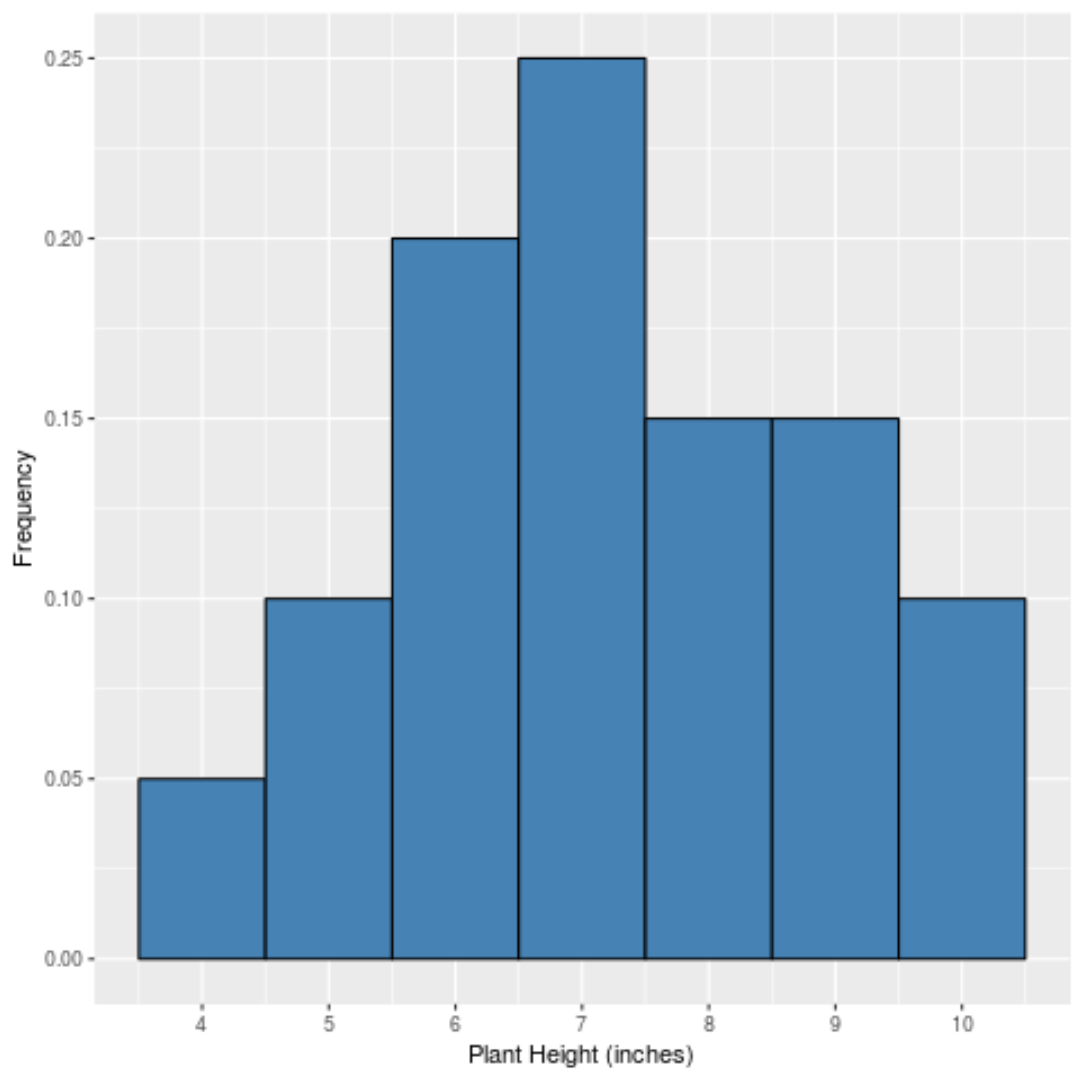
Die x-Achse zeigt den Datenwert und die y-Achse die relative Häufigkeit (z. B. erscheint der Wert „7“ 5 Mal von 20 Gesamtwerten im Datensatz, hat also eine relative Häufigkeit von 25 % bzw 0,25 .

Und wenn wir eine Dichtekurve erstellen würden, um die „Form“ dieser Verteilung zu erfassen, würde sie so aussehen:

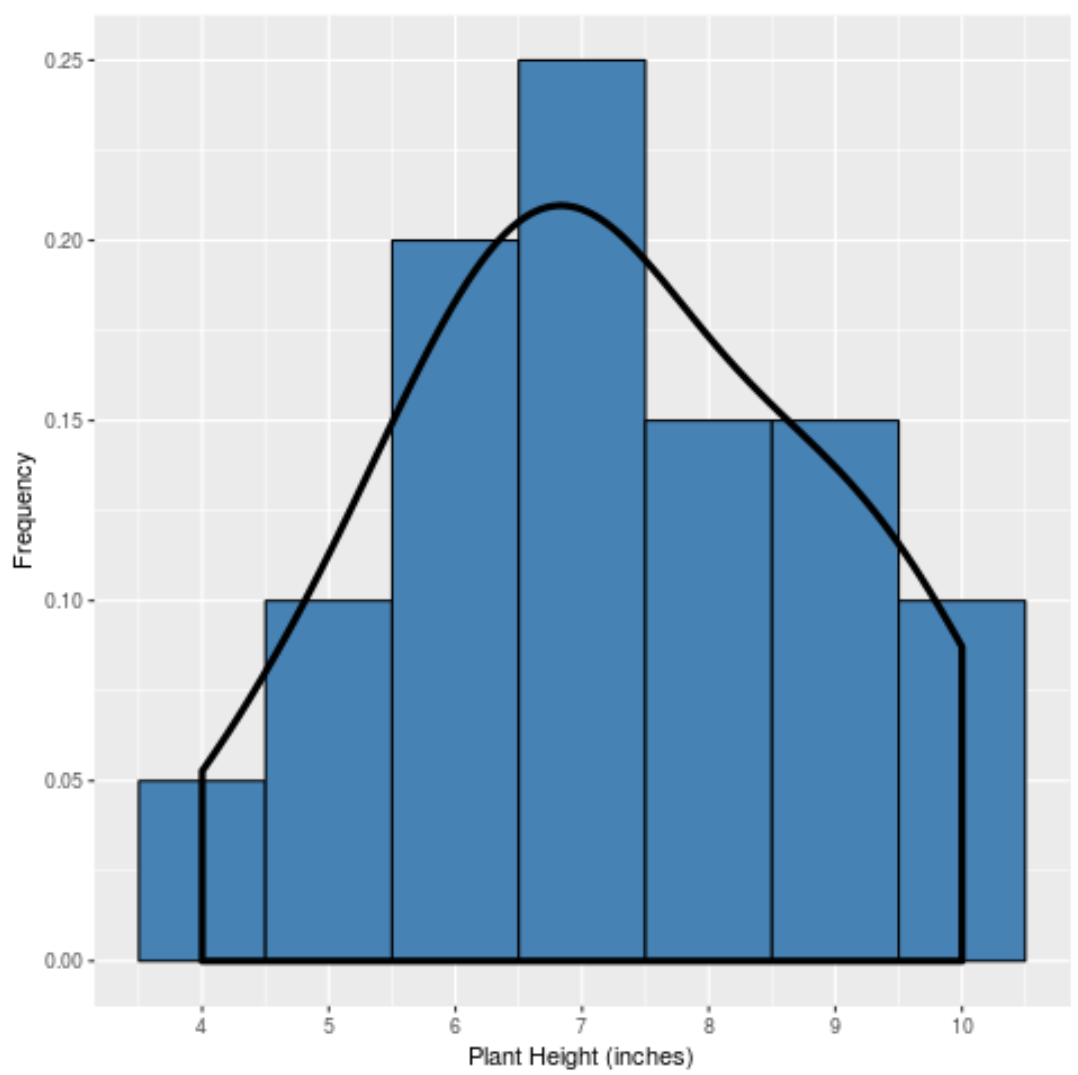
Die Kurve ist in der Nähe der Verteilungsmitte am höchsten, da dort die meisten Werte zu finden sind. Außerdem ist er an den Enden der Verteilung am niedrigsten, da weniger Pflanzen diese Werte annehmen (z. B. Höhe 4 Zoll oder 10 Zoll).

Wie man Dichtekurven interpretiert

Dichtekurven gibt es in allen Formen und Größen und sie ermöglichen uns ein schnelles visuelles Verständnis der Werteverteilung in einem bestimmten Datensatz. Sie sind besonders nützlich, um uns bei der Visualisierung zu helfen:

1. Asymmetrie

Schiefe ist eine Möglichkeit, die Symmetrie einer Verteilung zu beschreiben. Mithilfe von Dichtekurven können wir schnell erkennen, ob ein Diagramm nach links oder rechts geneigt ist oder keine Neigung aufweist:

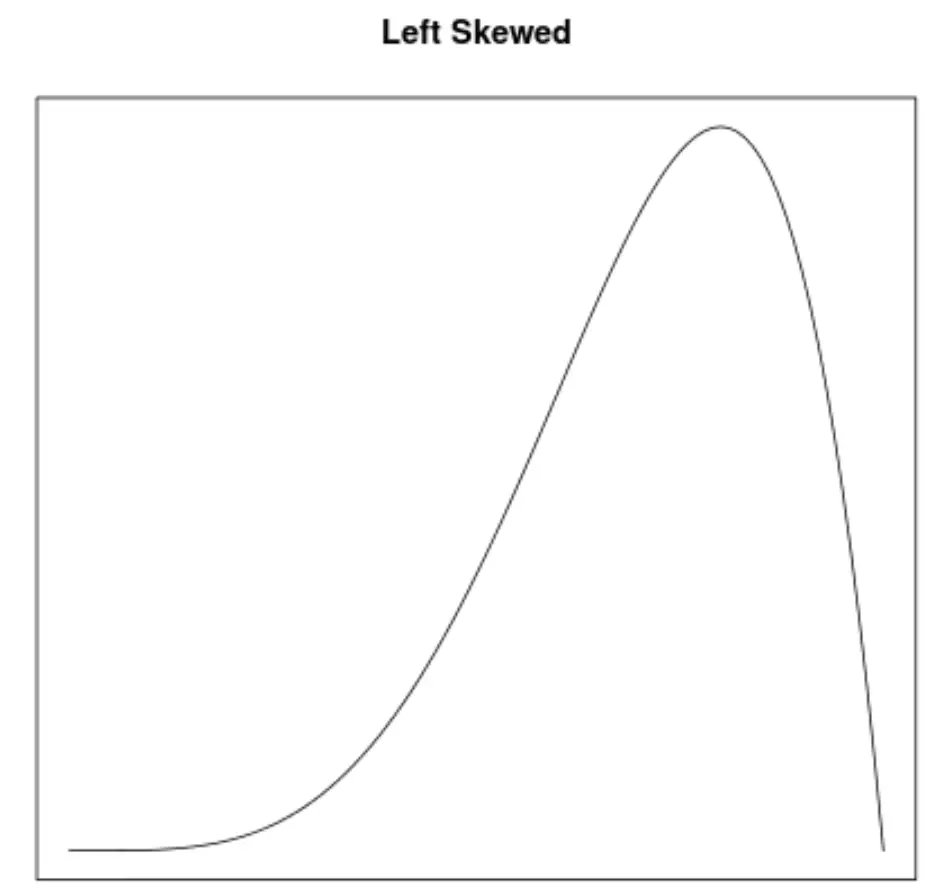
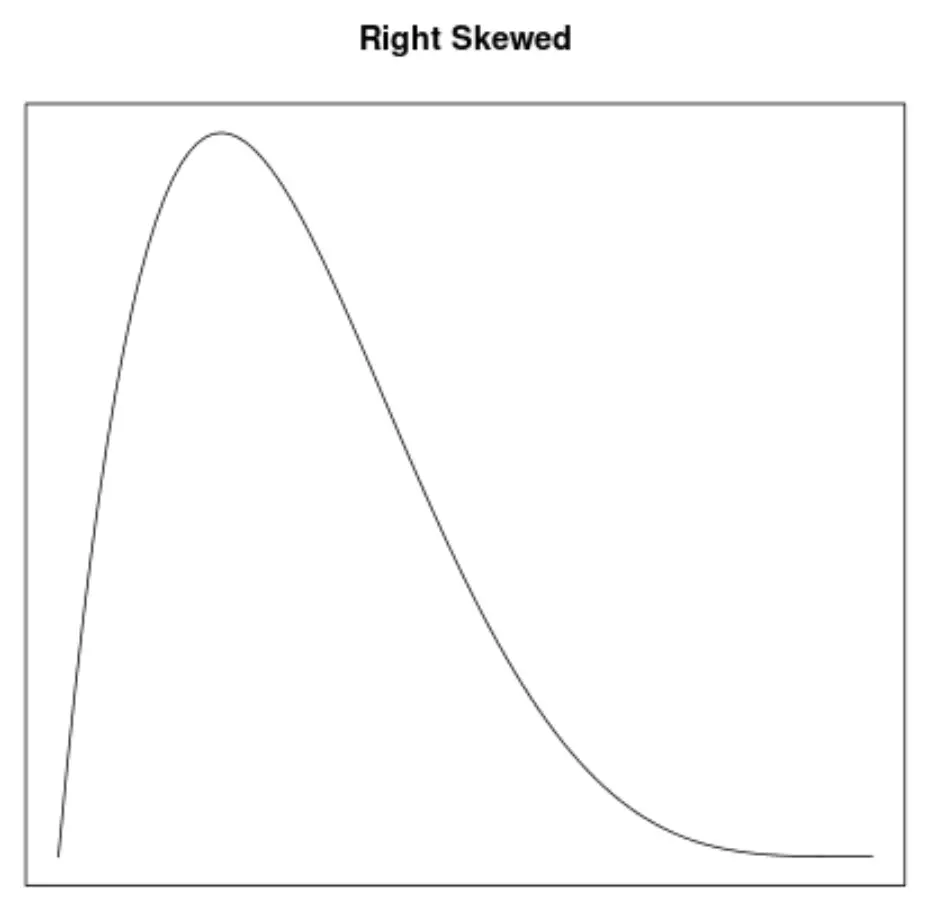
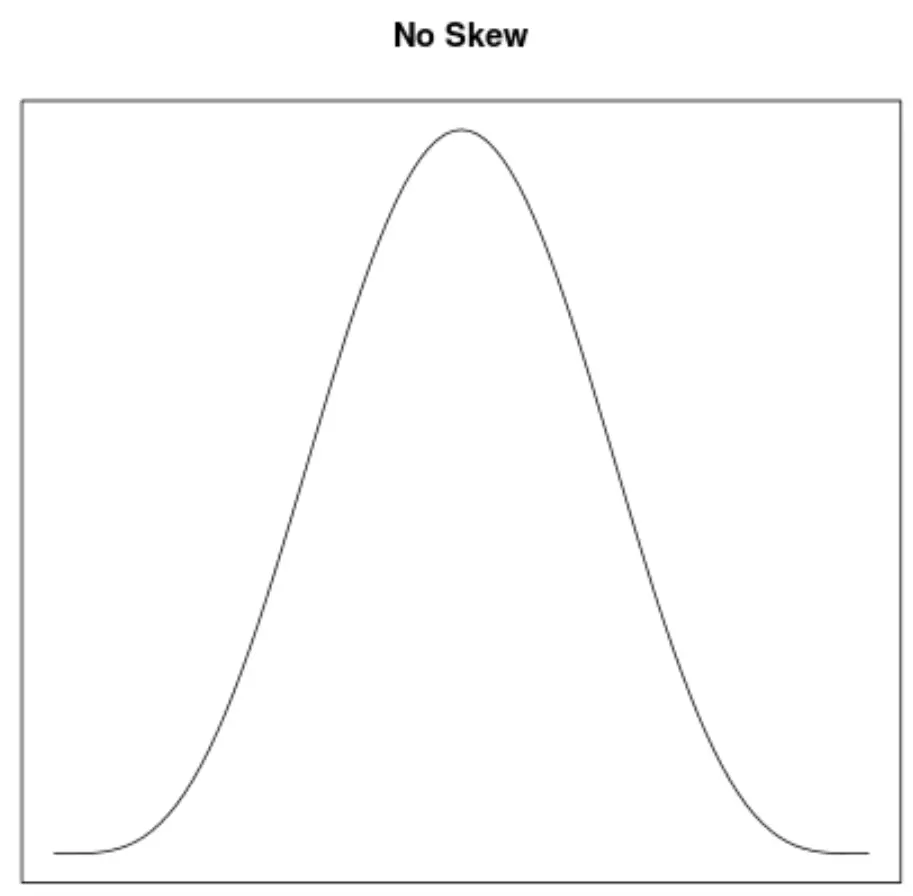
2. Die Lage des Mittelwerts und Medians

Anhand der Schiefe einer Dichtekurve können wir schnell erkennen, ob der Mittelwert oder Median in einer bestimmten Verteilung größer ist. Besonders:

• Bleibt eine Dichtekurve asymmetrisch , dann ist der Mittelwert niedriger als der Median.
• Wenn eine Dichtekurve rechtsschief ist, ist der Mittelwert größer als der Median.
• Wenn eine Dichtekurve keine Asymmetrie aufweist, ist der Mittelwert gleich dem Median.

3. Anzahl der Spitzen

Mithilfe von Dichtekurven können wir auch schnell erkennen, wie viele „Peaks“ es in einer bestimmten Verteilung gibt. In jedem der obigen Beispiele hatten die Verteilungen nur einen Peak, daher würden wir diese Verteilungen als unimodal beschreiben.

Einige Verteilungen können jedoch zwei Spitzen aufweisen, die wir bimodale Verteilungen nennen. Und in seltenen Fällen können wir auch multimodale Verteilungen mit zwei oder mehr Peaks haben.

Indem wir einfach eine Dichtekurve für einen bestimmten Datensatz erstellen, können wir schnell erkennen, wie viele Spitzen es in der Verteilung gibt.

Eigenschaften von Dichtekurven

Dichtekurven haben die folgenden Eigenschaften:

• Die Fläche unter der Kurve summiert sich immer zu 100 %.
• Die Kurve wird niemals unter die x-Achse fallen.

Berücksichtigen Sie diese beiden Tatsachen, wenn Sie Dichtekurven für verschiedene Verteilungen erstellen oder interpretieren.

Zusätzliche Ressourcen

Einführung in relative Häufigkeitshistogramme
So erstellen Sie eine Glockenkurve in Excel
So erstellen Sie eine Glockenkurve in Python