Erweiterter dickey-fuller-test in r (mit beispiel)

Eine Zeitreihe wird als „stationär“ bezeichnet, wenn sie keinen Trend aufweist, über die Zeit eine konstante Varianz aufweist und über die Zeit eine konstante Autokorrelationsstruktur aufweist.

Eine Möglichkeit zu testen, ob eine Zeitreihe stationär ist, besteht darin, einen erweiterten Dickey-Fuller-Test durchzuführen, der die folgenden Null- und Alternativhypothesen verwendet:

H ₀ : Die Zeitreihe ist instationär. Mit anderen Worten, seine Struktur hängt von der Zeit ab und seine Variation ist über die Zeit nicht konstant.

H _A : Die Zeitreihe ist stationär.

Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (z. B. α = 0,05), können wir die Nullhypothese ablehnen und daraus schließen, dass die Zeitreihe stationär ist.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie ein erweiterter Dickey-Fuller-Test in R für eine bestimmte Zeitreihe durchgeführt wird.

Beispiel: Augmented Dickey-Fuller-Test in R

Angenommen, wir haben die folgenden Zeitreihendaten in R:

 data <- c(3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10)

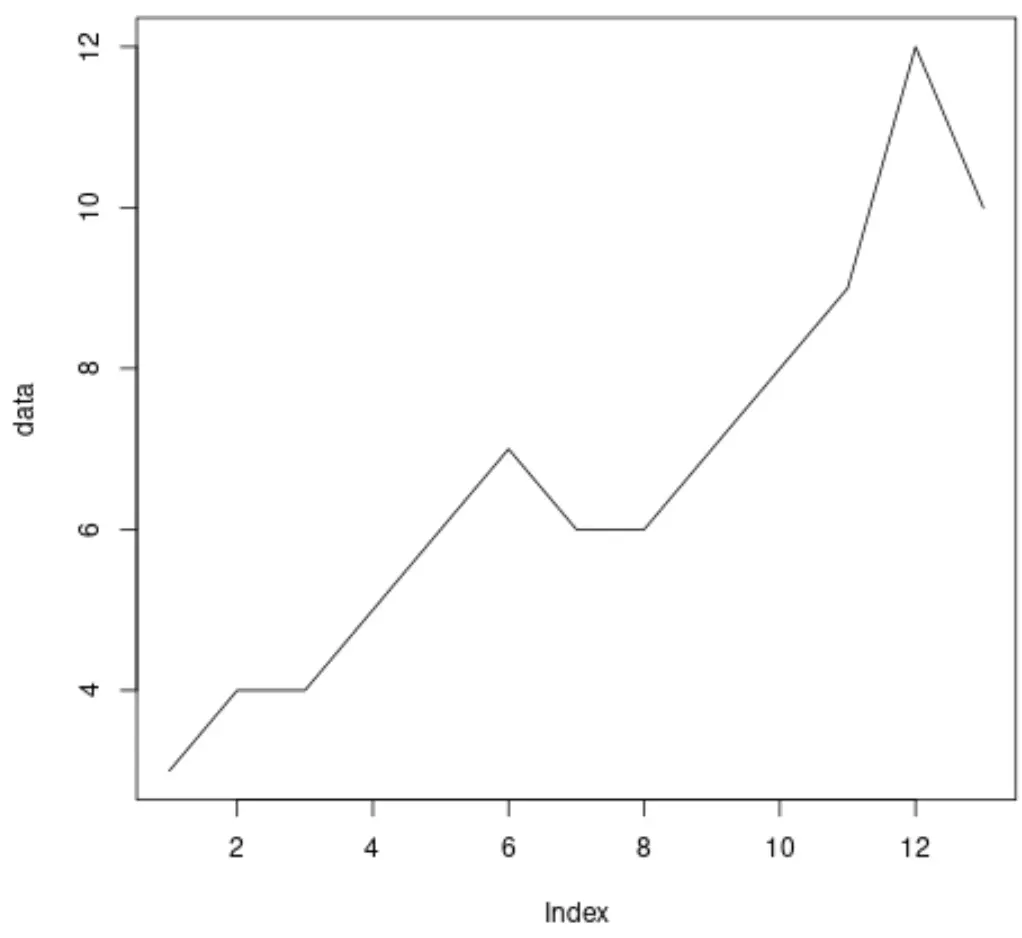
Bevor wir einen erweiterten Dickey-Fuller-Test an den Daten durchführen, können wir ein schnelles Diagramm erstellen, um die Daten zu visualisieren:

 plot(data, type=' l ')

Um einen erweiterten Dickey-Fuller-Test durchzuführen, können wir die Funktion adf.test() aus der tseries- Bibliothek verwenden.

Der folgende Code zeigt, wie diese Funktion verwendet wird:

 library (tseries)

#perform augmented Dickey-Fuller test 
adf.test(data)

	Augmented Dickey-Fuller Test

data:data
Dickey-Fuller = -2.2048, Lag order = 2, p-value = 0.4943
alternative hypothesis: stationary

So interpretieren Sie die wichtigsten Werte des Ergebnisses:

• Teststatistik: -2,2048
• P-Wert: 0,4943

Da der p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.

Dies bedeutet, dass die Zeitreihe nicht stationär ist. Mit anderen Worten, seine Struktur hängt von der Zeit ab und seine Variation ist über die Zeit nicht konstant.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in R ausführen:

So führen Sie einen Mann-Kendall-Trendtest in R durch
So zeichnen Sie eine Zeitreihe in R
So reduzieren Sie Datentrends