Die normalverteilung

Die Normalverteilung ist die häufigste Wahrscheinlichkeitsverteilung in der Statistik.

Normalverteilungen haben die folgenden Eigenschaften:

• Glockenform
• Symmetrisch
• Der Mittelwert und der Median sind gleich; beide liegen im Zentrum der Verteilung
• Etwa 68 % der Daten liegen innerhalb einer Standardabweichung vom Mittelwert
• Etwa 95 % der Daten liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
• Etwa 99,7 % der Daten liegen innerhalb von drei Standardabweichungen vom Mittelwert.

Die letzten drei Punkte werden als Faustregel bezeichnet, manchmal auch als 68-95-99,7-Regel bezeichnet.

Verwandte Themen: Faustregel (Übungsprobleme)

So zeichnen Sie eine Normalkurve

Um eine Normalkurve zu zeichnen, müssen wir den Mittelwert und die Standardabweichung kennen.

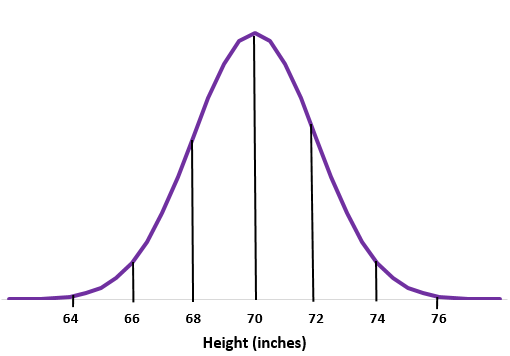
Beispiel 1: Angenommen, die Größe der Männer in einer bestimmten Schule ist normalverteilt mit einem Mittelwert von $\mu =\; 70\; Zoll\; und$ einer Standardabweichung von $\sigma \; =\; 2\; Zoll.\; Skizzieren\; Sie\; die\; Normalkurve.$

Schritt 1: Skizzieren Sie eine Normalkurve.

Schritt 2: Der Durchschnitt von 70 Zoll liegt in der Mitte.

Schritt 3: Jede Standardabweichung entspricht einem Abstand von 2 Zoll.

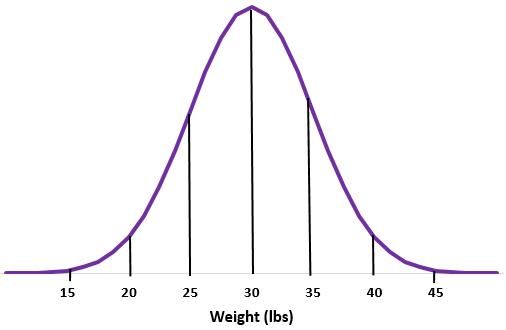
Beispiel 2: Angenommen, das Gewicht einer bestimmten Otterart ist normalverteilt mit einem Mittelwert von $\mu =\; 30\; lb\; und$ einer Standardabweichung von $\sigma \; =\; 5\; lb.\; Skizzieren\; Sie\; die\; Normalkurve.$

Schritt 1: Skizzieren Sie eine Normalkurve.

Schritt 2: Das durchschnittliche Gewicht von 30 Pfund liegt in der Mitte.

Schritt 3: Jede Standardabweichung entspricht einer Distanz von 5 Pfund

So finden Sie Prozentsätze mithilfe der Normalverteilung

Die Faustregel , manchmal auch 68-95-99,7-Regel genannt, besagt, dass für eine normalverteilte Zufallsvariable 68 % der Daten in den Bereich von einer Standardabweichung vom Mittelwert fallen, 95 % in den Bereich von zwei Standards Abweichungen vom Mittelwert und 99,7 % liegen innerhalb von drei Standardabweichungen vom Mittelwert.

Mit dieser Regel können wir Fragen zu Prozentsätzen beantworten.

Beispiel: Angenommen, die Größe der Männer in einer bestimmten Schule ist normalverteilt mit einem Mittelwert von $\mu =\; 70\; Zoll\; und$ einer Standardabweichung von $\sigma \; =\; 2\; Zoll.$

$Wie\; viel\; Prozent\; der\; Männer\; an\; dieser\; Schule\; sind\; ungefähr\; über\; 74\; Zoll\; groß?$

Lösung:

Schritt 1: Skizzieren Sie eine Normalverteilung mit einem Mittelwert von $\mu =\; 70\; Zoll\; und$ einer Standardabweichung von $\sigma \; =\; 2\; Zoll.$

Schritt 2: Eine Körpergröße von 74 Zoll liegt zwei Standardabweichungen über dem Durchschnitt. Addieren Sie die Prozentsätze über diesem Punkt zur Normalverteilung.

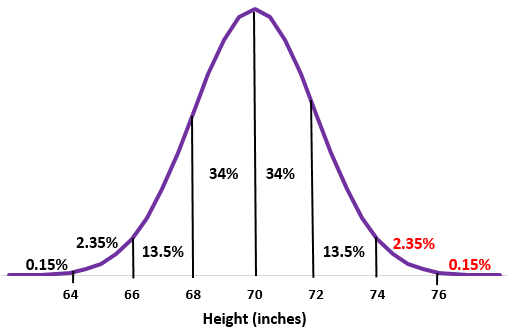
2,35 % + 0,15 % = 2,5 %

Etwa 2,5 % der Männer an dieser Schule sind über 74 Zoll groß.

$Wie\; viel\; Prozent\; der\; Männer\; an\; dieser\; Schule\; sind\; ungefähr\; zwischen\; 68\; und\; 72\; Zoll\; groß?$

Lösung:

Schritt 1: Skizzieren Sie eine Normalverteilung mit einem Mittelwert von $\mu =\; 70\; Zoll\; und$ einer Standardabweichung von $\sigma \; =\; 2\; Zoll.$

Schritt 2: Eine Körpergröße von 68 Zoll und 72 Zoll liegt eine Standardabweichung unter bzw. über dem Durchschnitt. Addieren Sie einfach die Prozentsätze zwischen diesen beiden Punkten in der Normalverteilung.

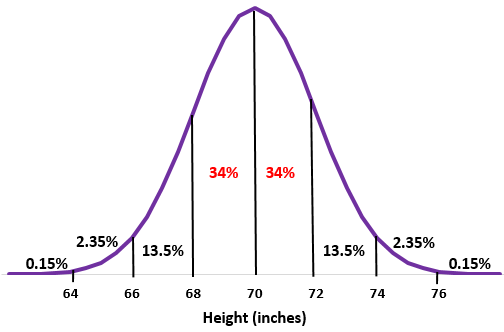
34 % + 34 % = 68 %

Etwa 68 % der Männer an dieser Schule sind zwischen 68 und 72 Zoll groß.

So finden Sie Zählungen mithilfe der Normalverteilung

Wir können die Faustregel auch verwenden, um Fragen zu Zählungen zu beantworten.

Beispiel: Angenommen, das Gewicht einer bestimmten Otterart ist normalverteilt mit einem Mittelwert von $\mu =\; 30\; lb\; und$ einer Standardabweichung von $\sigma \; =\; 5\; lb.$

Eine bestimmte Kolonie hat 200 dieser Otter. Wie viele dieser Otter wiegen ungefähr mehr als 35 Pfund?

Lösung:

Schritt 1: Skizzieren Sie eine Normalverteilung mit einem Mittelwert von $\mu =\; 30\; lb\; und$ einer Standardabweichung von $\sigma \; =\; 5\; lb.$

Schritt 2: Ein Gewicht von 35 Pfund liegt eine Standardabweichung über dem Mittelwert. Addieren Sie die Prozentsätze über diesem Punkt zur Normalverteilung.

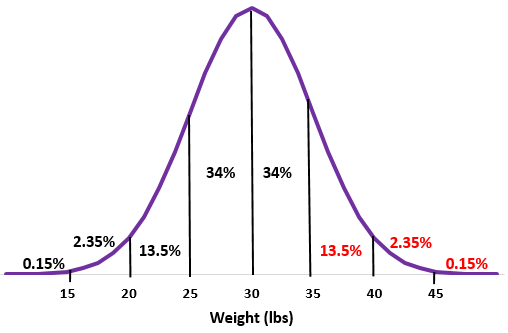
13,5 % + 2,35 % + 0,15 % = 16 %

Schritt 3: Da es in der Kolonie 200 Otter gibt, sind 16 % von 200 = 0,16 * 200 = 32

Ungefähr 32 Otter in dieser Kolonie wiegen mehr als 35 Pfund.

Wie viele Otter in dieser Kolonie wiegen ungefähr weniger als 30 Pfund?

Anstatt alle Schritte zu befolgen, die wir oben ausgeführt haben, können wir erkennen, dass der Median einer Normalverteilung gleich dem Mittelwert ist, der in diesem Fall 30 Pfund beträgt.

Das bedeutet, dass die Hälfte der Otter mehr als 30 Pfund und die andere Hälfte weniger als 30 Pfund wiegt. Das bedeutet, dass 50 % der 200 Otter weniger als 30 Pfund wiegen, also 0,5 * 200 = 100 Otter .

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur Normalverteilung:

6 konkrete Beispiele der Normalverteilung
Normalverteilung vs. t-Verteilung: der Unterschied
So erstellen Sie eine Glockenkurve in Excel
So erstellen Sie eine Glockenkurve in Python