Kann die varianz negativ sein?

In der Statistik bezieht sich der Begriff Varianz darauf, wie Werte in einem bestimmten Datensatz verteilt sind.

Eine häufige Frage, die Studierende zum Thema Varianz stellen, ist:

Kann die Varianz negativ sein?

Die Antwort: Nein, die Varianz kann nicht negativ sein. Der niedrigste Wert, den es annehmen kann, ist Null.

Um zu verstehen, warum das so ist, müssen wir verstehen, wie die Varianz tatsächlich berechnet wird.

So berechnen Sie die Lücke

Die Formel zum Ermitteln der Varianz einer Stichprobe (bezeichnet mit s ² ) lautet:

s ² = Σ (x _i – x ) ² / (n-1)

Gold:

• x : Das Stichprobenmittel
• x _i : Die ^i-te Beobachtung in der Stichprobe
• N : Stichprobengröße
• Σ : Ein griechisches Symbol mit der Bedeutung „Summe“

Angenommen, wir haben den folgenden Datensatz mit 10 Werten:

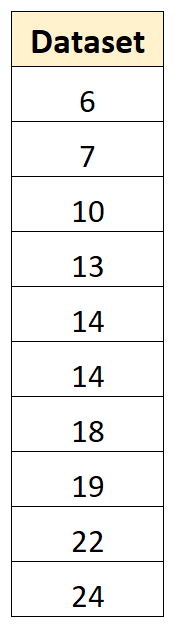
Mit den folgenden Schritten können wir die Varianz dieser Stichprobe berechnen:

Schritt 1: Finden Sie den Durchschnitt

Der Durchschnitt ist einfach der Durchschnitt. Es ergibt sich ein Wert von 14,7 .

Schritt 2: Ermitteln Sie die quadratischen Abweichungen

Dann können wir die quadratische Abweichung jedes einzelnen Wertes vom Mittelwert berechnen.

Die erste quadratische Abweichung wird beispielsweise als (6-14,7) ² = 75,69 berechnet.

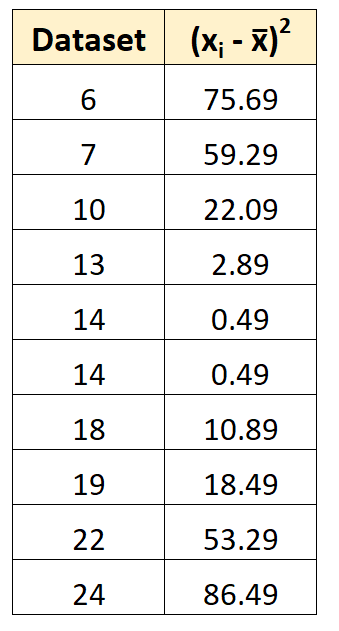
Schritt 3: Ermitteln Sie die Summe der quadrierten Abweichungen

Dann können wir alle Quadrate der Abweichungen summieren:

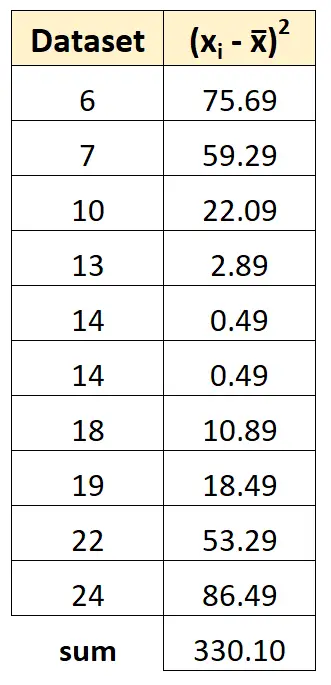
Schritt 4: Berechnen Sie die Stichprobenvarianz

Schließlich können wir die Stichprobenvarianz als Summe der quadratischen Abweichungen dividiert durch (n-1) berechnen:

s ² = 330,1 / (10-1) = 330,1 / 9 = 36,678

Die Stichprobenvarianz beträgt 36.678 .

Ein Beispiel für eine Nullvarianz

Die einzige Möglichkeit für einen Datensatz, eine Varianz von Null zu haben, besteht darin, dass alle Werte im Datensatz gleich sind .

Der folgende Datensatz hat beispielsweise eine Stichprobenvarianz von Null:

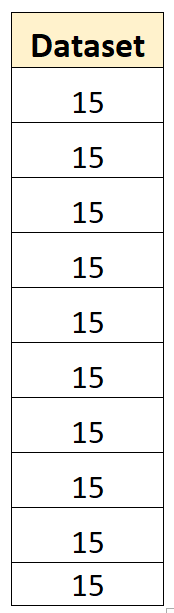
Der Mittelwert des Datensatzes liegt bei 15 und keiner der Einzelwerte weicht vom Mittelwert ab. Somit ist die Summe der Quadrate der Abweichungen Null und die Stichprobenvarianz ist einfach Null.

Kann die Standardabweichung negativ sein?

Eine gebräuchlichere Methode zur Messung der Werteverteilung in einem Datensatz ist die Verwendung der Standardabweichung, die einfach die Quadratwurzel der Varianz ist.

Wenn beispielsweise die Varianz einer bestimmten Stichprobe ^s2 = 36,678 beträgt, wird die Standardabweichung (geschrieben s ) wie folgt berechnet:

s = √ ^s2 = √ 36,678 = 6,056

Da wir bereits wissen, dass die Varianz immer Null oder eine positive Zahl ist, bedeutet dies, dass die Standardabweichung niemals negativ sein kann, da die Quadratwurzel aus Null oder einer positiven Zahl nicht negativ sein kann.

Zusätzliche Ressourcen

Maße der zentralen Tendenz: Definition und Beispiele
Streuungsmaße: Definition und Beispiele