Was sind disjunkte ereignisse? (definition & beispiele)

Disjunkte Ereignisse sind Ereignisse, die nicht gleichzeitig auftreten können.

In probabilistischer Notation geschrieben sind die Ereignisse A und B disjunkt, wenn ihr Schnittpunkt Null ist. Dies kann wie folgt geschrieben werden:

• P(A und B) = 0
• P(A∩B) = 0

Angenommen, wir wählen zufällig eine Karte aus einem Stapel aus. Sei Ereignis A das Ereignis, dass die Karte ein Pik oder ein Kreuz ist, und Ereignis B das Ereignis, dass die Karte ein Herz oder eine Karo ist.

Wir würden den Beispielraum für Ereignisse wie folgt definieren:

• A = {Spaten, Schläger}
• B = {Herz, Diamant}

Beachten Sie, dass es keine Überlappung zwischen den beiden abgetasteten Räumen gibt. Somit sind die Ereignisse A und B disjunkte Ereignisse, da sie nicht beide gleichzeitig auftreten können.

Hinweis: Disjunkte Ereignisse werden auch als gegenseitig ausschließend bezeichnet.

Beispiele für disjunkte Ereignisse

Hier sind einige weitere Beispiele für disjunkte Ereignisse.

Beispiel 1: Zeichnen

Angenommen, Sie werfen eine Münze. Sei Ereignis A das Ereignis, bei dem die Münze auf „Kopf“ landet, und Ereignis B das Ereignis, bei dem die Münze auf „Kopf“ landet.

Ereignis A und Ereignis B wären disjunkt, da sie nicht beide gleichzeitig auftreten können. Die Münze kann weder auf Kopf noch auf Zahl landen.

Beispiel 2: Würfeln

Angenommen, Sie würfeln. Sei Ereignis A das Ereignis, bei dem der Würfel auf einer ungeraden Zahl landet, und Ereignis B sei das Ereignis, bei dem der Würfel auf einer geraden Zahl landet.

Ereignis A und Ereignis B wären disjunkt, da sie nicht beide gleichzeitig auftreten können. Die Würfel können weder auf eine gerade noch auf eine ungerade Zahl fallen.

Beispiel 3: Pro Bowl-Standort

Angenommen, die NFL möchte einen Ort für die Ausrichtung des Pro Bowls auswählen. Sie haben die Optionen in Miami und San Diego eingegrenzt. Sie stecken die beiden Namen in einen Hut und wählen zufällig einen aus. Nehmen wir an, dass Event A das Event ist, für das sie Miami auswählen, und Event B das Event, für das sie San Diego auswählen.

Ereignis A und Ereignis B wären disjunkt, da sie nicht beide gleichzeitig auftreten können. Miami und San Diego können beide nicht ausgewählt werden.

Disjunkte Ereignisse anzeigen

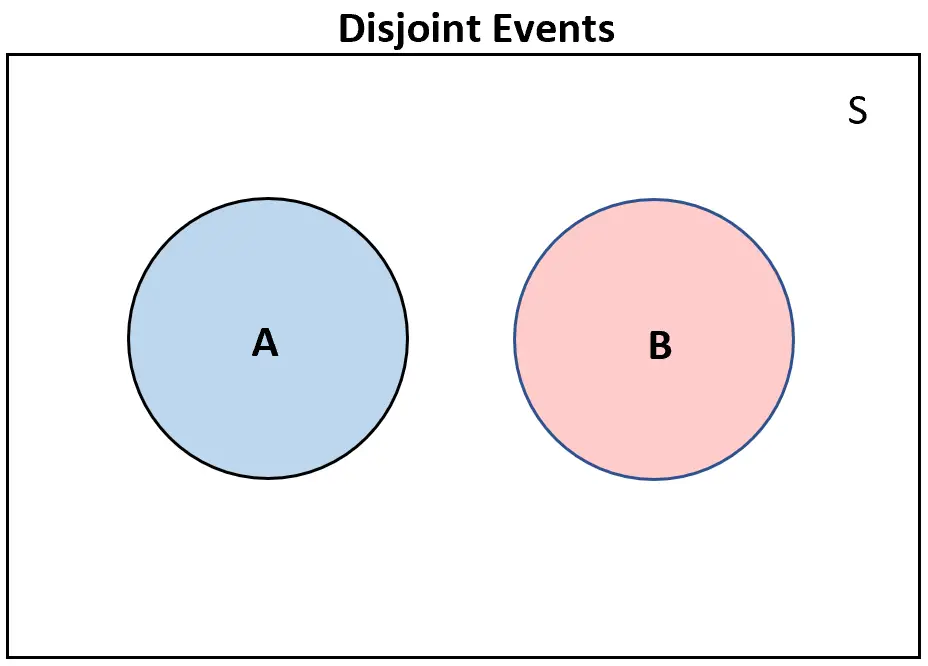
Eine nützliche Möglichkeit, disjunkte Ereignisse zu visualisieren, ist die Erstellung eines Venn-Diagramms.

Wenn zwei Ereignisse disjunkt sind, überlappen sie sich in einem Venn-Diagramm überhaupt nicht:

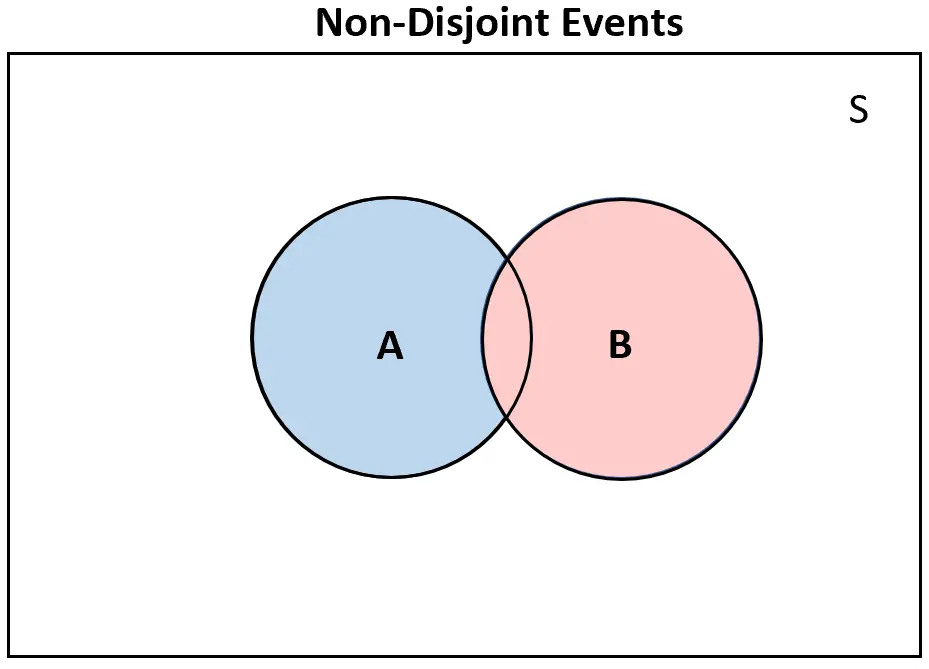
Wenn umgekehrt zwei Ereignisse nicht disjunkt sind , wird es im Venn-Diagramm zumindest eine gewisse Überlappung geben:

Die Wahrscheinlichkeit disjunkter Ereignisse

Wie bereits erwähnt, ist die Wahrscheinlichkeit, dass beide Ereignisse gleichzeitig auftreten, null, wenn zwei Ereignisse disjunkt sind.

• P(A∩B) = 0

Ebenso kann die Wahrscheinlichkeit des Eintretens eines Ereignisses berechnet werden, indem die einzelnen Wahrscheinlichkeiten addiert werden.

• P(A∪B) = P(A) + P(B)

Angenommen, Ereignis A sei das Ereignis, bei dem ein Würfel auf einer 1 oder einer 2 landet, und Ereignis B sei das Ereignis, bei dem ein Würfel auf einer 5 oder einer 6 landet.

Wir würden den Beispielraum für Ereignisse wie folgt definieren:

• A = {1, 2}
• B = {5, 6}

Wir würden die Wahrscheinlichkeit des Eintretens von Ereignis A oder Ereignis B wie folgt berechnen:

• P(A∪B) = P(A) + P(B)
• P(A∪B) = 2/6 + 2/6
• P(A∪B) = 4/6 = 2/3

Die Wahrscheinlichkeit, dass Ereignis A oder Ereignis B eintritt, beträgt 2/3 .

Zusätzliche Ressourcen

Die folgenden Tutorials bieten Erläuterungen zu anderen gängigen Wahrscheinlichkeitsthemen:

So ermitteln Sie die Wahrscheinlichkeit von A oder B: anhand von Beispielen
So ermitteln Sie die Wahrscheinlichkeit von A und B: Mit Beispielen
Gesetz der Gesamtwahrscheinlichkeit: Definition und Beispiele