Diskrete gleichverteilung

In diesem Artikel wird erläutert, was die diskrete Gleichverteilung ist und wie ihre charakteristische Formel lautet. Ebenso können Sie die grafische Darstellung der diskreten Gleichverteilung und ihrer Eigenschaften sehen.

Was ist eine diskrete Gleichverteilung?

Eine diskrete Gleichverteilung ist eine diskrete Wahrscheinlichkeitsverteilung, bei der alle Werte gleich wahrscheinlich sind, d. h. in einer diskreten Gleichverteilung haben alle Werte die gleiche Eintrittswahrscheinlichkeit.

Beispielsweise kann der Wurf eines Würfels mit einer diskreten Gleichverteilung definiert werden, da alle möglichen Ergebnisse (1, 2, 3, 4, 5 oder 6) die gleiche Eintrittswahrscheinlichkeit haben.

Im Allgemeinen verfügt eine diskrete Gleichverteilung über zwei charakteristische Parameter, a und b , die den Bereich möglicher Werte definieren, den die Verteilung annehmen kann. Wenn also eine Variable durch eine diskrete Gleichverteilung definiert ist, wird sie als Uniform(a,b) geschrieben.

Die diskrete Gleichverteilung kann zur Beschreibung von Zufallsexperimenten verwendet werden, denn wenn alle Ergebnisse die gleiche Wahrscheinlichkeit haben, bedeutet dies, dass das Experiment zufällig ist.

Diskrete Gleichverteilungsformel

Nachdem wir nun die Definition der diskreten Gleichverteilung kennen, werden wir sehen, welche Formel es uns ermöglicht, die Wahrscheinlichkeit des Auftretens der Werte einer Verteilung dieses Typs zu berechnen.

Die Wahrscheinlichkeitsfunktion einer diskreten Gleichverteilung ist konstant und ihr Wert ist über die Gesamtzahl der möglichen Ergebnisse gleich eins. Somit lautet die Formel für die diskrete Gleichverteilung wie folgt:

Andererseits lautet die Formel für die kumulative Wahrscheinlichkeitsfunktion der diskreten Gleichverteilung wie folgt:

Gold

Und

sind die charakteristischen Parameter der diskreten Gleichverteilung.

Diskretes Gleichverteilungsdiagramm

Da die diskrete Gleichverteilung in einem Intervall nur bestimmte Werte annehmen kann, besteht ihre grafische Darstellung aus Punkten. Darüber hinaus sind alle Wahrscheinlichkeiten gleich, sodass alle Punkte in der diskreten Gleichverteilung dieselben vertikalen Koordinaten haben.

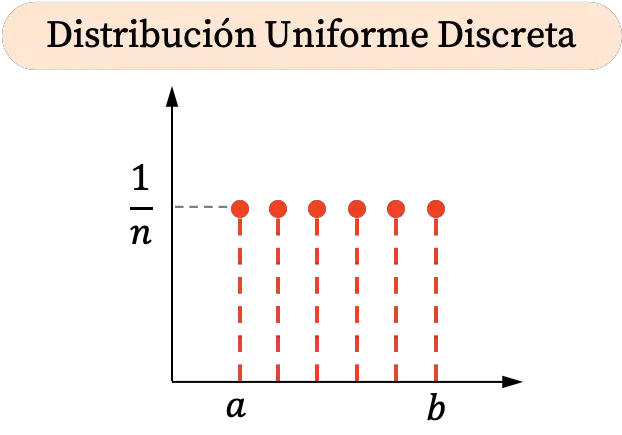
Andererseits sieht das kumulative Wahrscheinlichkeitsdiagramm der diskreten Gleichverteilung wie folgt aus:

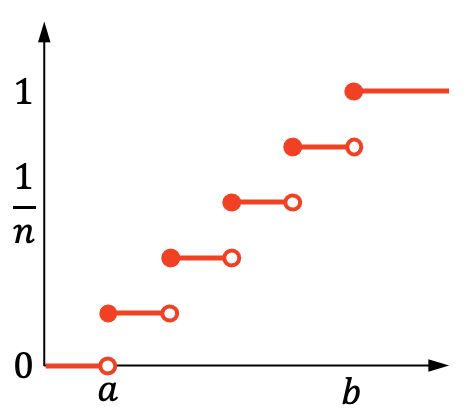
Merkmale der diskreten Gleichverteilung

Die diskrete Gleichverteilung weist folgende Merkmale auf:

• Die diskrete Gleichverteilung wird durch zwei ganzzahlige Parameter a und b definiert, die den Bereich möglicher Werte der Verteilung bestimmen.

• Der Mittelwert einer diskreten Gleichverteilung ist gleich der Summe ihrer beiden charakteristischen Parameter dividiert durch zwei.

• Der Median einer diskreten Gleichverteilung entspricht ihrem Mittelwert und wird daher mit demselben Ausdruck berechnet:

• Die Varianz einer diskreten Gleichverteilung ist gleich dem Quadrat der Gesamtzahl der Ergebnisse minus eins dividiert durch zwölf.

• Die diskrete Gleichverteilung ist symmetrisch zu ihrem Mittelwert, daher ist der Schiefekoeffizient dieser Wahrscheinlichkeitsverteilung Null.

• Die Kurtosis der diskreten Gleichverteilung kann mit dem folgenden Ausdruck berechnet werden:

Diskrete Gleichverteilung und kontinuierliche Gleichverteilung

Schließlich werden wir sehen, was der Unterschied zwischen einer diskreten Gleichverteilung und einer kontinuierlichen Gleichverteilung ist, da es sich um zwei ähnliche Arten von Wahrscheinlichkeitsverteilungen handelt, die sich jedoch erheblich unterscheiden.

Der Unterschied zwischen einer diskreten Gleichverteilung und einer kontinuierlichen Gleichverteilung liegt in ihren möglichen Werten. Die diskrete Gleichverteilung kann in einem Intervall nur bestimmte Werte annehmen, während die kontinuierliche Gleichverteilung in dem Intervall, in dem sie definiert ist, jeden Wert annehmen kann.

Im Allgemeinen können diskrete Gleichverteilungen nur ganzzahlige Werte annehmen, während kontinuierliche Gleichverteilungen auch Dezimalwerte annehmen können.