Dreifaktorielle anova: definition und beispiel

Eine dreifache ANOVA wird verwendet, um zu bestimmen, wie sich drei verschiedene Faktoren auf eine Antwortvariable auswirken.

Dreifaktorielle ANOVAs sind weniger verbreitet als eine einfaktorielle ANOVA (mit nur einem Faktor) oder eine zweifaktorielle ANOVA (mit nur zwei Faktoren), werden aber dennoch in einer Vielzahl von Bereichen verwendet.

Wann immer wir eine Drei-Wege-ANOVA durchführen, möchten wir wissen, ob zwischen jedem Faktor und der Antwortvariablen eine statistisch signifikante Beziehung besteht und ob es Interaktionseffekte zwischen den Faktoren gibt.

Dieses Tutorial zeigt mehrere Szenarien, in denen Sie eine dreifaktorielle ANOVA verwenden können, sowie ein Beispiel für deren Durchführung.

Wann sollte eine Drei-Wege-ANOVA verwendet werden?

Hier sind einige Szenarien, in denen Sie eine Drei-Wege-ANOVA verwenden können:

Szenario 1: Botanik

Ein Botaniker möchte möglicherweise bestimmen, wie (1) Sonneneinstrahlung, (2) Bewässerungshäufigkeit und (3) Düngertyp das Pflanzenwachstum beeinflussen.

In diesem Szenario könnte sie eine Drei-Wege-ANOVA durchführen, da es drei Faktoren und eine Antwortvariable gibt.

Szenario 2: Einzelhandel

Ein Manager eines Einzelhandelsgeschäfts möchte möglicherweise ermitteln, wie sich (1) der Wochentag, (2) der Geschäftsstandort und (3) Werbekampagnen auf den Gesamtumsatz auswirken.

In diesem Szenario könnte er eine Drei-Wege-ANOVA durchführen, da es drei Faktoren und eine Antwortvariable gibt.

Szenario 3: Medizinisch

Ein Arzt möchte möglicherweise feststellen, wie sich (1) das Geschlecht, (2) die Ernährung und (3) die Trainingsgewohnheiten auf das Gewicht auswirken.

In diesem Szenario könnte sie eine Drei-Wege-ANOVA durchführen, da es drei Faktoren und eine Antwortvariable gibt.

Dreifaktorielle ANOVA: Beispiel

Angenommen, ein Forscher möchte herausfinden, ob Trainingsprogramm, Geschlecht und Sportart die Sprunghöhe beeinflussen.

Um dies zu testen, kann er eine Drei-Wege-ANOVA mit den folgenden Faktoren durchführen:

• 1. Trainingsprogramm (Programm 1 vs. Programm 2)
• 2. Geschlecht (männlich oder weiblich)
• 3. Sportabteilung (Division I vs. Division II)

Die einzige Antwortvariable ist die Sprunghöhe .

Angenommen, er sammelt diese Daten von 40 Personen:

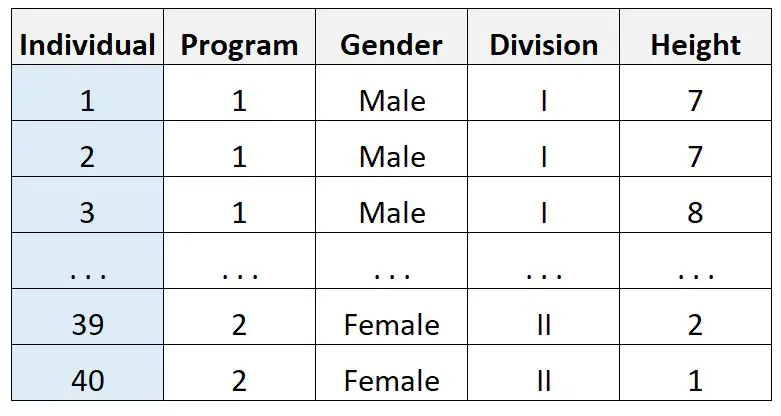
Anschließend führt er mithilfe einer Statistiksoftware eine Drei-Wege-ANOVA durch und erhält das folgende Ergebnis:

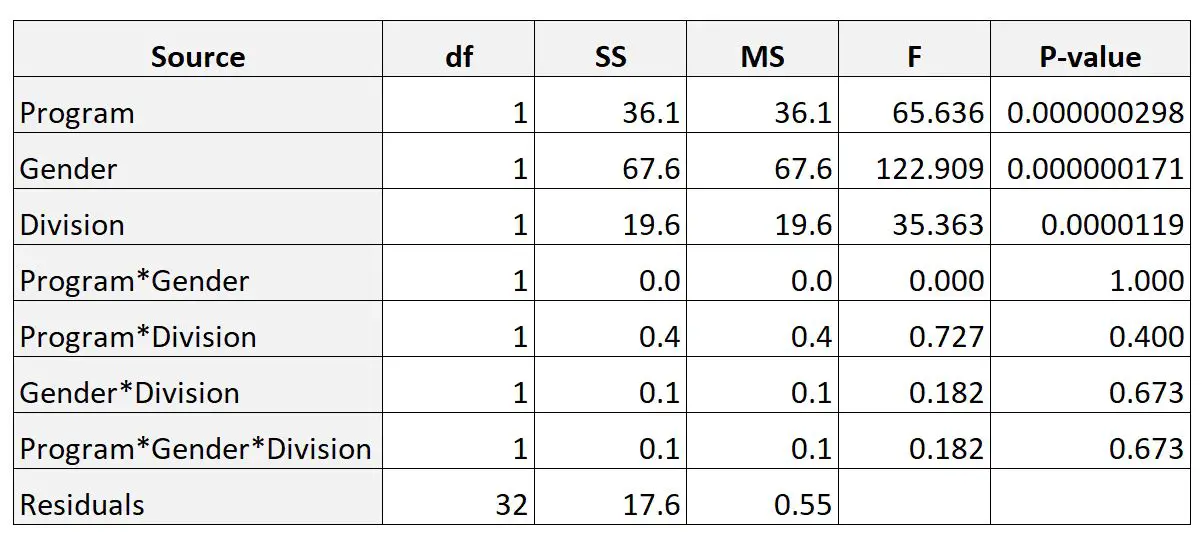
In der Spalte „P-Wert“ werden der P-Wert für jeden einzelnen Faktor und die Wechselwirkungen zwischen den Faktoren angezeigt.

Anhand der Ergebnisse können wir erkennen, dass keine der Wechselwirkungen zwischen den drei Faktoren statistisch signifikant war.

Wir können auch sehen, dass jeder der drei Faktoren (Programm, Geschlecht und Abteilung) statistisch signifikant war.

Zusammenfassend würden wir sagen, dass Trainingsprogramm, Geschlecht und Spielklasse allesamt wichtige Indikatoren für eine erhöhte Sprunghöhe bei Spielern sind.

Wir würden auch sagen, dass es keine signifikanten Wechselwirkungen zwischen diesen drei Faktoren gibt.

Hinweis : In der Praxis würden wir auch die durchschnittliche Sprunghöhe für jedes Programm, Geschlecht und jede Abteilung berechnen, damit wir bestimmen können, welche Stufen der einzelnen Faktoren mit einer Erhöhung der Sprunghöhe verbunden sind.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie eine Drei-Wege-ANOVA in R und Python durchgeführt wird:

So führen Sie eine Drei-Wege-ANOVA in R durch
So führen Sie eine Drei-Wege-ANOVA in Python durch