Eine einführung in die dreiecksverteilung

Die Dreiecksverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung mit einer dreieckigen Wahrscheinlichkeitsdichtefunktion.

Es wird durch drei Werte definiert:

• Der Mindestwert hat
• Der Maximalwert b
• Der Maximalwert c

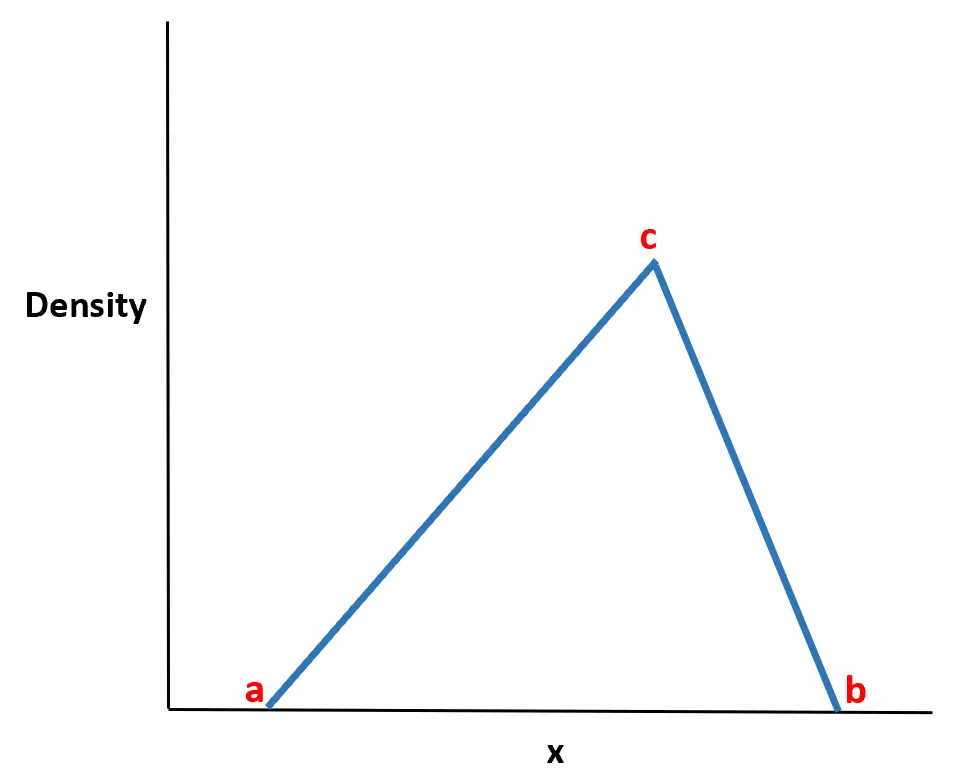
Der Name der Verteilung rührt daher, dass die Wahrscheinlichkeitsdichtefunktion die Form eines Dreiecks hat.

Es stellt sich heraus, dass diese Verteilung in der realen Welt äußerst nützlich ist, da wir häufig den Mindestwert (a), den Höchstwert (b) und den wahrscheinlichsten Wert (c) schätzen können, den eine Zufallsvariable annehmen wird. kann das Verhalten von Zufallsvariablen häufig mithilfe einer Dreiecksverteilung modellieren, wenn nur diese drei Werte bekannt sind.

Beispielsweise kann ein Restaurant davon ausgehen, dass sein Gesamtumsatz für die kommende Woche mindestens 10.000 US-Dollar, höchstens 30.000 US-Dollar und höchstwahrscheinlich 25.000 US-Dollar betragen wird.

Anhand dieser drei Zahlen könnten sie mithilfe einer Dreiecksverteilung die Wahrscheinlichkeit bestimmen, eine bestimmte Anzahl von Verkäufen zu tätigen.

Eigenschaften der Dreiecksverteilung

Die Dreiecksverteilung hat folgende Eigenschaften:

PDF:

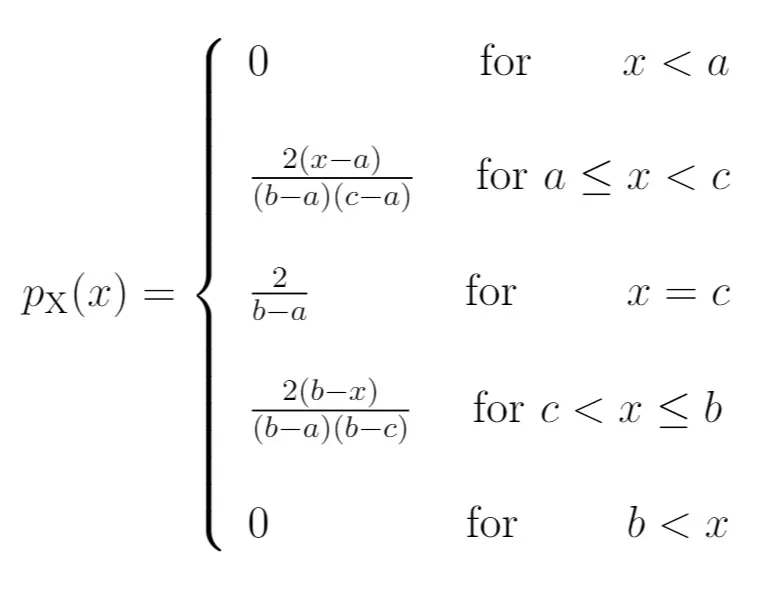
CDF:

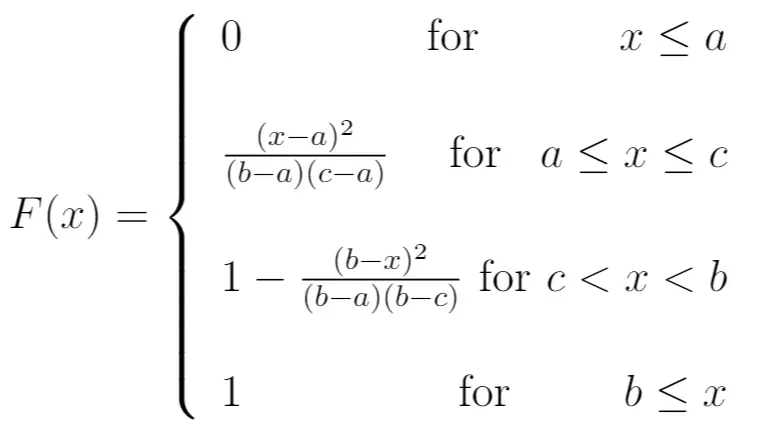
Durchschnitt: (a + b + c) / 3

Modus: c

Varianz: (a ² + b ² + c ² – ab – ac – bc) / 18

Beispiel für die Verwendung der Dreiecksverteilung

Kehren wir zum vorherigen Beispiel zurück. Nehmen wir an, ein Restaurant schätzt, dass sein Gesamtumsatz für die kommende Woche mindestens 10.000 US-Dollar, maximal 30.000 US-Dollar und höchstwahrscheinlich 25.000 US-Dollar betragen wird.

Wie hoch ist die Wahrscheinlichkeit, dass das Restaurant einen Gesamtumsatz von weniger als 20.000 US-Dollar erzielt?

Um diese Frage zu beantworten, können wir x = Gesamtumsatz fragen. Wir wissen, dass x zwischen dem Mindestwert a von 10.000 $ und dem Maximalwert c von 25.000 $ liegt.

Laut PDF können wir also die folgende Gleichung verwenden, um die Wahrscheinlichkeit zu ermitteln, dass das Restaurant einen Gesamtumsatz von weniger als 20.000 US-Dollar erzielt:

• P(X < 20.000 $) = (xa) ² / ((ba)(ca))
• P(X < 20.000 $) = (20.000-10.000) ² / ((30.000-10.000)(25.000-10.000))
• P(X < 20.000 $) = 0,333

Die Wahrscheinlichkeit, dass das Restaurant einen Gesamtumsatz von weniger als 20.000 US-Dollar erzielt, beträgt 0,333 .

Wie hoch ist der durchschnittlich erwartete Umsatz des Restaurants?

Wir können den erwarteten Durchschnittsumsatz mithilfe der zuvor angegebenen Formel für den Durchschnitt berechnen:

• Durchschnitt = (a + b + c) / 3
• Durchschnitt = (10.000 $ + 30.000 $ + 25.000 $) / 3
• Durchschnitt = 21.667 $

Der durchschnittliche erwartete Umsatz liegt bei 21.667 .

Zusätzliche Ressourcen

Die folgenden Tutorials bieten Einführungen in andere häufig verwendete Distributionen:

Die Normalverteilung
Die Binomialverteilung
Die Fischverteilung
Die geometrische Verteilung