Verwendung der dreiecksverteilung in r (mit beispielen)

Die Dreiecksverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung mit einer dreieckigen Wahrscheinlichkeitsdichtefunktion.

Es wird durch drei Werte definiert:

• Der Mindestwert hat
• Der Maximalwert b
• Der Maximalwert c

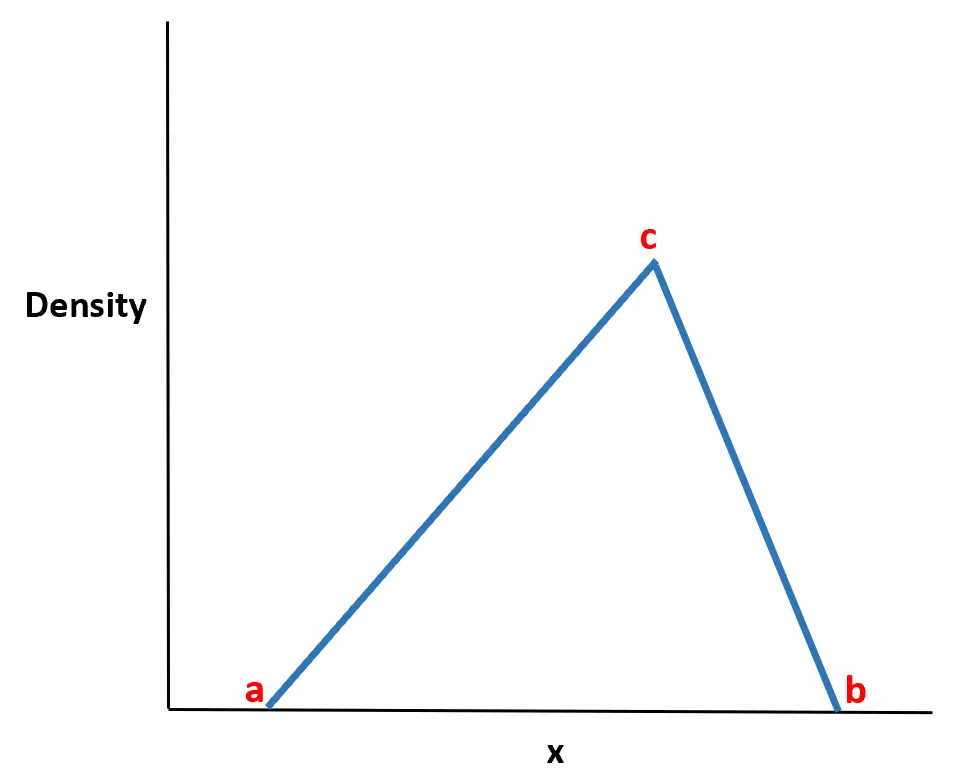
Um die Wahrscheinlichkeiten der Dreiecksverteilung in R zu berechnen, können wir die Funktion ptri( ) aus dem EnvStats- Paket verwenden, die die folgende Syntax verwendet:

ptri(q, min = 0, max = 1, Modus = 1/2)

Gold:

• q : Quantil von Interesse
• min : Der Mindestwert der Verteilung
• max : Der Maximalwert der Verteilung
• Modus : Der Spitzenwert der Verteilung

Die folgenden Beispiele zeigen, wie man diese Funktion in R praktisch nutzen kann.

Beispiel 1: Berechnung einer Wahrscheinlichkeit, die kleiner als ein bestimmter Wert ist

Nehmen wir an, ein Restaurant schätzt, dass sein Gesamtumsatz für die kommende Woche mindestens 10.000 US-Dollar, maximal 30.000 US-Dollar und höchstwahrscheinlich 25.000 US-Dollar betragen wird.

Wie hoch ist die Wahrscheinlichkeit, dass das Restaurant einen Gesamtumsatz von weniger als 20.000 US-Dollar erzielt?

Wir können den folgenden Code verwenden, um diese Wahrscheinlichkeit zu berechnen:

 library (EnvStats)

#calculate probability
ptri(q = 20000, min = 10000, max = 30000, mode = 25000)

[1] 0.3333333

Die Wahrscheinlichkeit, dass das Restaurant einen Gesamtumsatz von weniger als 20.000 US-Dollar erzielt, beträgt 0,333 .

Beispiel 2: Berechnung einer Wahrscheinlichkeit, die größer als ein bestimmter Wert ist

Nehmen wir an, ein Geschäft schätzt, dass die Anzahl der Kunden, die in einer bestimmten Woche kommen, mindestens 500, maximal 2.000 und höchstwahrscheinlich 1.200 beträgt.

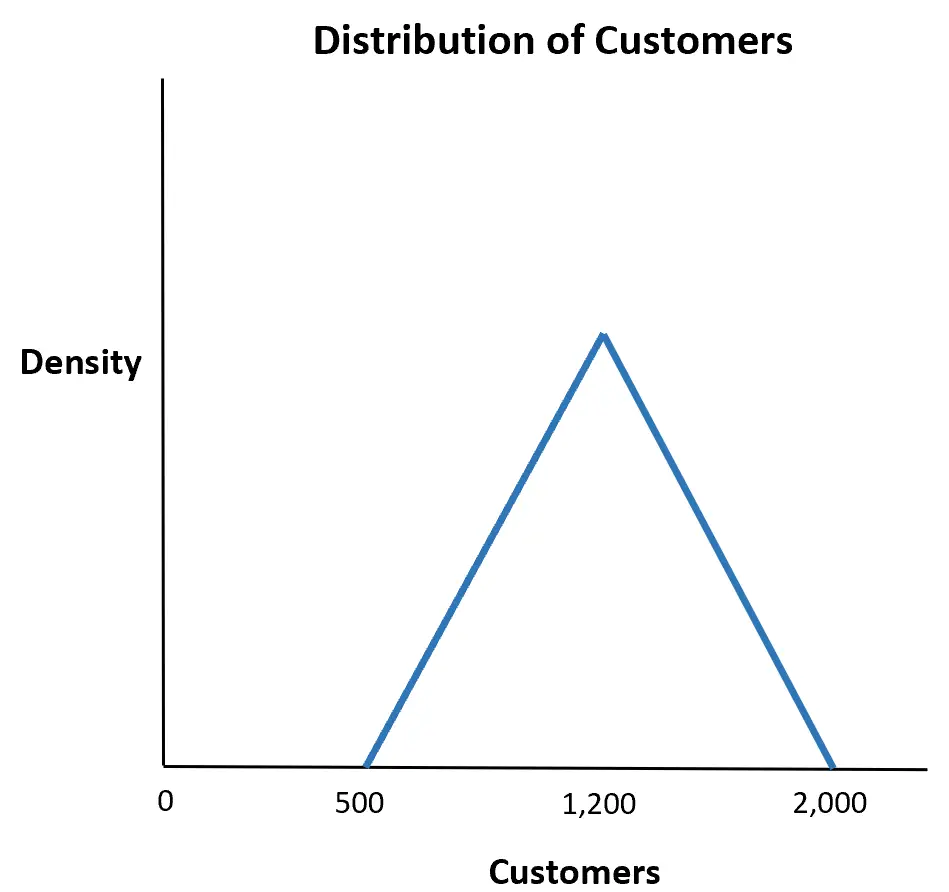
Wie groß ist die Wahrscheinlichkeit, dass in einer Woche mehr als 1.500 Kunden den Laden betreten?

Wir können den folgenden Code verwenden, um diese Wahrscheinlichkeit zu berechnen:

 library (EnvStats)

#calculate probability
1 - ptri(q = 1500, min = 500, max = 2000, mode = 1200)

[1] 0.2083333

Die Wahrscheinlichkeit, dass mehr als 1.500 Kunden den Laden betreten, liegt bei etwa 0,208.

Hinweis : Die vollständige Dokumentation zur ptri()- Funktion finden Sie hier .

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie man andere Wahrscheinlichkeitsverteilungen in R verwendet:

So verwenden Sie die Normalverteilung in R
Wie man die Binomialverteilung in R verwendet
So verwenden Sie die Poisson-Verteilung in R
Wie man die Multinomialverteilung in R verwendet