So führen sie den dunnett-test in r durch
EinPost-hoc-Test ist eine Art Test, der im Anschluss an eine ANOVA durchgeführt wird, um zu bestimmen, welche Gruppenmittelwerte sich statistisch signifikant voneinander unterscheiden.
Wenn eine der Studiengruppen als Kontrollgruppe betrachtet wird, sollten wir den Dunnett-Test als Post-hoc-Test verwenden.
In diesem Tutorial wird erklärt, wie der Dunnett-Test in R durchgeführt wird.
Beispiel: Dunnett-Test in R
Angenommen, eine Lehrerin möchte wissen, ob zwei neue Lerntechniken das Potenzial haben, die Testergebnisse ihrer Schüler zu verbessern. Um dies zu testen, teilt sie ihre Klasse mit 30 Schülern nach dem Zufallsprinzip in die folgenden drei Gruppen ein:
- Kontrollgruppe: 10 Studierende
- Neues technisches Studium 1: 10 Studierende
- Neues technisches Studium 2: 10 Studierende
Nachdem jeder Schüler eine Woche lang die ihm zugewiesene Lerntechnik angewendet hat, legt er die gleiche Prüfung ab.
Wir können die folgenden Schritte in R verwenden, um einen Datensatz zu erstellen, die Gruppenmittelwerte zu visualisieren, eine einfaktorielle ANOVA durchzuführen und schließlich den Dunnett-Test durchzuführen, um zu bestimmen, welche neue Studientechnik (falls vorhanden) im Vergleich zur Kontrollgruppe unterschiedliche Ergebnisse liefert .
Schritt 1: Erstellen Sie den Datensatz.
Der folgende Code zeigt, wie man einen Datensatz erstellt, der die Prüfungsergebnisse aller 30 Studenten enthält:
#create data frame data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ), score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89, 81, 82, 83, 83, 83, 84, 87, 90, 92, 93, 77, 78, 79, 88, 89, 90, 91, 95, 95, 98)) #view first six rows of data frame head(data) technical score 1 control 76 2 controls 77 3 controls 77 4 controls 81 5 controls 82 6 controls 82
Schritt 2: Prüfungsergebnisse für jede Gruppe anzeigen.
Der folgende Code zeigt, wie Boxplots erstellt werden, um die Verteilung der Prüfungsergebnisse für jede Gruppe zu visualisieren:
boxplot(score ~ technique,
data = data,
main = "Exam Scores by Studying Technique",
xlab = "Studying Technique",
ylab = "Exam Scores",
col = "steelblue",
border = "black")
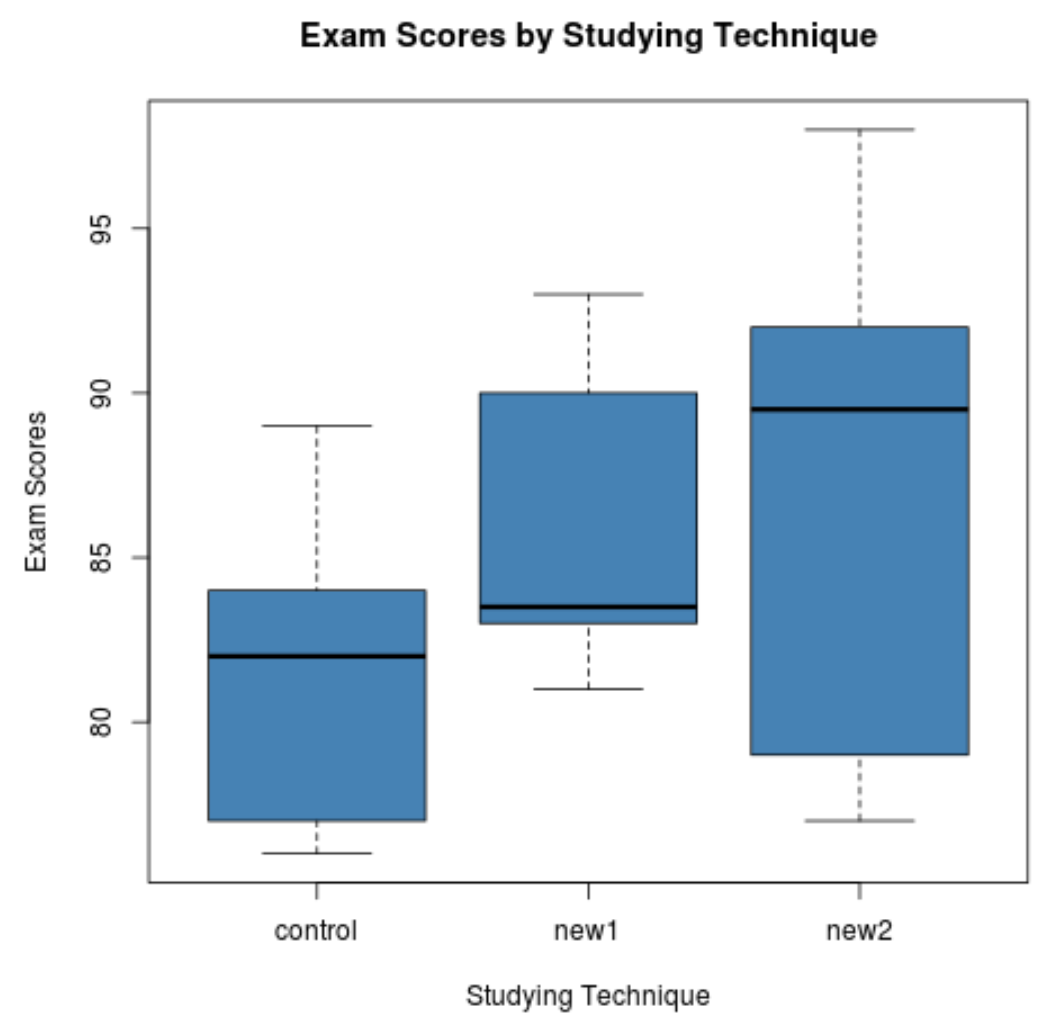
Allein anhand der Boxplots können wir erkennen, dass die Verteilung der Prüfungsergebnisse für jede Lerntechnik sehr unterschiedlich ist. Anschließend führen wir eine einfaktorielle ANOVA durch, um festzustellen, ob diese Unterschiede statistisch signifikant sind.
Verwandte Themen: So zeichnen Sie mehrere Boxplots in einem einzelnen Diagramm in R
Schritt 3: Führen Sie eine einfaktorielle ANOVA durch.
Der folgende Code zeigt, wie eine einfaktorielle ANOVA durchgeführt wird, um Unterschiede zwischen den durchschnittlichen Prüfungsergebnissen in jeder Gruppe zu testen:
#fit the one-way ANOVA model model <- aov(score ~ technique, data = data) #view model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) technical 2 211.5 105.73 3.415 0.0476 * Residuals 27 836.0 30.96 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Da der Gesamt-p-Wert ( 0,0476 ) kleiner als 0,05 ist, weist dies darauf hin, dass nicht jede Gruppe die gleiche durchschnittliche Prüfungspunktzahl aufweist. Als nächstes führen wir den Dunnett-Test durch, um festzustellen, welche Lerntechnik zu durchschnittlichen Prüfungsergebnissen führt, die sich von denen der Kontrollgruppe unterscheiden.
Schritt 4: Führen Sie den Dunnett-Test durch.
Um den Dunnett-Test in R durchzuführen, können wir die Funktion DunnettTest() aus der DescTools- Bibliothek verwenden, die die folgende Syntax verwendet:
Dunnett-Test(x, g)
Gold:
- x: ein numerischer Vektor von Datenwerten (z. B. Prüfungsergebnisse)
- g: Ein Vektor, der die Namen von Gruppen angibt (z. B. Lerntechnik)
Der folgende Code zeigt, wie diese Funktion für unser Beispiel verwendet wird:
#load DescTools library library(DescTools) #perform Dunnett's Test DunnettTest(x=data$score, g=data$technique) Dunnett's test for comparing several treatments with a control: 95% family-wise confidence level $control diff lwr.ci upr.ci pval new1-control 4.2 -1.6071876 10.00719 0.1787 new2-control 6.4 0.5928124 12.20719 0.0296 * --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1
Das Ergebnis lässt sich wie folgt interpretieren:
- Der durchschnittliche Unterschied in den Prüfungsergebnissen zwischen der neuen Lernmethode 1 und der Kontrollgruppe beträgt 4,2. Der entsprechende p-Wert beträgt 0,1787 .
- Der durchschnittliche Unterschied in den Prüfungsergebnissen zwischen der neuen Lerntechnik 2 und der Kontrollgruppe beträgt 6,4. Der entsprechende p-Wert beträgt 0,0296 .
Anhand der Ergebnisse können wir erkennen, dass das Studium von Technik 2 die einzige Technik ist, die zu mittleren Prüfungsergebnissen führt, die sich deutlich (p = 0,0296) von denen der Kontrollgruppe unterscheiden.
Zusätzliche Ressourcen
Eine Einführung in die einfaktorielle ANOVA
So führen Sie eine einfaktorielle ANOVA in R durch
So führen Sie den Tukey-Test in R durch