Absolute mittlere abweichung versus standardabweichung: was ist der unterschied?

Die Standardabweichung ist eine der gebräuchlichsten Methoden zur Messung der Streuung eines Datensatzes.

Es wird wie folgt berechnet:

Standardabweichung = √( Σ(x _i – x ) ² / n )

Eine weitere Möglichkeit, die Verteilung von Beobachtungen in einem Datensatz zu messen, ist die mittlere absolute Abweichung .

Es wird wie folgt berechnet:

Durchschnittliche absolute Abweichung = Σ|x _i – x | /nicht

In diesem Tutorial werden die Unterschiede zwischen diesen beiden Metriken erläutert und Beispiele für die jeweilige Berechnung gegeben.

Ähnlichkeiten und Unterschiede

Wie der Name schon sagt, versuchen Standardabweichung und mittlere absolute Abweichung, die typische Abweichung von Beobachtungen vom Mittelwert in einem bestimmten Datensatz zu quantifizieren.

Die von jeder Metrik verwendete Methode ist jedoch unterschiedlich.

Standardabweichung

Die Standardabweichung ermittelt die quadrierte Differenz zwischen jeder Beobachtung und dem Mittelwert eines Datensatzes. Anschließend werden diese quadrierten Differenzen gemittelt und die Quadratwurzel gezogen.

Damit erhalten wir eine Zahl, die den „Standard“ oder die typische Abweichung einer Beobachtung vom Mittelwert darstellt.

Bedeutet absolute Abweichung

Umgekehrt ermittelt die mittlere absolute Abweichung die absolute Abweichung zwischen jeder Beobachtung und dem Mittelwert des Datensatzes. Anschließend wird der Durchschnitt dieser Abweichungen ermittelt.

Damit erhalten wir eine Zahl, die die durchschnittliche Abweichung der Beobachtungen vom Mittelwert darstellt.

Da die Standardabweichung quadratische Unterschiede findet, ist sie immer gleich oder größer als die mittlere absolute Abweichung.

Bei extremen Ausreißern ist die Standardabweichung deutlich größer als die mittlere absolute Abweichung. Das folgende Beispiel verdeutlicht diesen Punkt.

Beispiel: durchschnittliche absolute Abweichung von der Standardabweichung

Angenommen, wir haben den folgenden Datensatz mit 8 Werten:

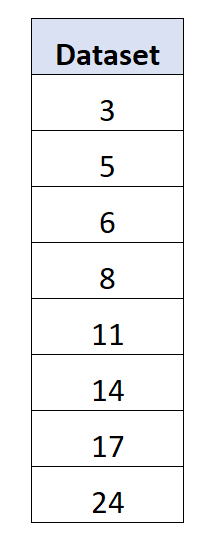
Der Durchschnitt liegt bei 11 .

Wir würden also die durchschnittliche absolute Abweichung wie folgt berechnen:

Durchschnittliche absolute Abweichung = (|3-11| + |5-11| + |6-11| + |8-11| + |11-11| + |14-11| + |17-11| + |24- 11|) / 8 = 5,5 .

Und wir würden die Standardabweichung wie folgt berechnen:

Standardabweichung = √((3-11) ² + (5-11) ² + (6-11) ² + (8-11) ² + (11-11) ² + (14-11) ² + (17- 11) ² + (24-11) ² )/8) = 6,595 .

Wie bereits erwähnt, ist die Standardabweichung immer gleich oder größer als die mittlere absolute Abweichung.

Allerdings wird der Unterschied zwischen der Standardabweichung und der mittleren absoluten Abweichung besonders groß sein, wenn es extreme Ausreißer im Datensatz gibt.

Betrachten Sie beispielsweise den folgenden Datensatz mit einem extremen Ausreißer für den letzten Wert:

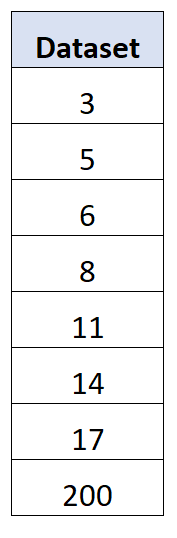
Es stellt sich heraus, dass die Standardabweichung für diesen Datensatz 63,27 beträgt, während die durchschnittliche absolute Abweichung 41,75 beträgt.

Der extreme Ausreißer führt dazu, dass die Standardabweichung viel größer ist als die mittlere absolute Abweichung.