Effektgröße: was es ist und warum es wichtig ist
„Die statistische Signifikanz ist das Uninteressanteste an den Ergebnissen. Sie müssen Ergebnisse anhand von Größenordnungen beschreiben – nicht nur, wie sich eine Behandlung auf Menschen auswirkt, sondern auch, wie sehr sie sich auf sie auswirkt. -Gene V. Glass
In der Statistik verwenden wir häufig p-Werte , um festzustellen, ob zwischen zwei Gruppen ein statistisch signifikanter Unterschied besteht.
Nehmen wir zum Beispiel an, wir möchten wissen, ob zwei unterschiedliche Lerntechniken zu unterschiedlichen Testergebnissen führen. Wir haben also eine Gruppe von 20 Studierenden, die eine Lerntechnik verwenden, um sich auf eine Prüfung vorzubereiten, während eine andere Gruppe von 20 Studierenden eine andere Lerntechnik verwendet. Anschließend geben wir jedem Schüler den gleichen Test.
Nachdem wir einen t-Test bei zwei Stichproben durchgeführt haben, um einen Mittelwertunterschied zu ermitteln, stellen wir fest, dass der p-Wert für den Test 0,001 beträgt. Wenn wir ein Signifikanzniveau von 0,05 verwenden, bedeutet dies, dass zwischen den mittleren Ergebnissen der beiden Gruppen ein statistisch signifikanter Unterschied besteht. Die Lerntechnik hat also einen Einfluss auf die Testergebnisse.
Der p-Wert sagt uns zwar, dass die Lerntechnik einen Einfluss auf die Testergebnisse hat, er sagt uns jedoch nicht, wie groß dieser Einfluss ist. Um dies zu verstehen, müssen wir die Effektgröße kennen.
Was ist Effektgröße?
Eine Effektgröße ist eine Möglichkeit, den Unterschied zwischen zwei Gruppen zu quantifizieren.
Während uns ein p-Wert sagen kann, ob zwischen zwei Gruppen ein statistisch signifikanter Unterschied besteht oder nicht, kann uns eine Effektgröße sagen , wie groß dieser Unterschied tatsächlich ist. In der Praxis sind Effektgrößen viel interessanter und nützlicher als p-Werte.
Abhängig von der Art der Analyse, die Sie durchführen, gibt es drei Möglichkeiten, die Effektgröße zu messen:
1. Standardisierte Mittelwertdifferenz
Wenn Sie die mittlere Differenz zwischen zwei Gruppen untersuchen möchten, ist die Verwendung einer standardisierten mittleren Differenz die geeignete Methode zur Berechnung der Effektgröße. Die am häufigsten verwendete Formel ist Cohens d und wird wie folgt berechnet:
Cohens D = ( x1 – x2 )/ s
Dabei sind x 1 und x 2 die Stichprobenmittelwerte von Gruppe 1 bzw. Gruppe 2 und s ist die Standardabweichung der Grundgesamtheit, aus der die beiden Gruppen gezogen wurden.
Mit dieser Formel lässt sich die Effektgröße leicht interpretieren:
- Ein d von 1 gibt an, dass sich die Mittelwerte der beiden Gruppen um eine Standardabweichung unterscheiden.
- Ein d von 2 bedeutet, dass sich die Gruppenmittelwerte um zwei Standardabweichungen unterscheiden.
- Ein d von 2,5 gibt an, dass sich die beiden Mittelwerte um 2,5 Standardabweichungen unterscheiden, und so weiter.
Eine andere Möglichkeit, die Effektgröße zu interpretieren, ist: Eine Effektgröße von 0,3 bedeutet, dass der Wert der durchschnittlichen Person in Gruppe 2 0,3 Standardabweichungen über dem Personendurchschnitt von Gruppe 1 liegt und daher den Wert von 62 % derjenigen der Gruppe 1 übertrifft. .
Die folgende Tabelle zeigt verschiedene Effektgrößen und ihre entsprechenden Perzentile:
| Effektgröße | Prozentsatz der Gruppe 2 , der unter dem Durchschnitt der Personen in Gruppe 1 liegen würde |
|---|---|
| 0,0 | 50 % |
| 0,2 | 58 % |
| 0,4 | 66 % |
| 0,6 | 73 % |
| 0,8 | 79 % |
| 1,0 | 84 % |
| 1.2 | 88 % |
| 1.4 | 92 % |
| 1.6 | 95 % |
| 1.8 | 96 % |
| 2,0 | 98 % |
| 2.5 | 99 % |
| 3,0 | 99,9 % |
Je größer die Effektgröße, desto größer ist der Unterschied zwischen dem durchschnittlichen Individuum in jeder Gruppe.
Im Allgemeinen gilt ein d von 0,2 oder weniger als kleine Effektgröße, ein d von etwa 0,5 als mittlere Effektgröße und ein d von 0,8 oder mehr als große Effektgröße.
Wenn sich die Mittelwerte zweier Gruppen also nicht um mindestens 0,2 Standardabweichungen unterscheiden, ist der Unterschied unbedeutend, selbst wenn der p-Wert statistisch signifikant ist.
2. Korrelationskoeffizient
Wenn Sie die quantitative Beziehung zwischen zwei Variablen untersuchen möchten, wird die Effektgröße am häufigsten mithilfe des Pearson-Korrelationskoeffizienten berechnet. Es ist ein Maß für den linearen Zusammenhang zwischen zwei Variablen X und Y. Es hat einen Wert zwischen -1 und 1, wobei:
- -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
- 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
- 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an
Die Formel zur Berechnung des Pearson-Korrelationskoeffizienten ist recht komplex, kann aber für Interessierte hier nachgelesen werden.
Je weiter der Korrelationskoeffizient von Null entfernt ist, desto stärker ist die lineare Beziehung zwischen zwei Variablen. Dies lässt sich auch anhand eines einfachen Streudiagramms der Werte der Variablen X und Y erkennen.
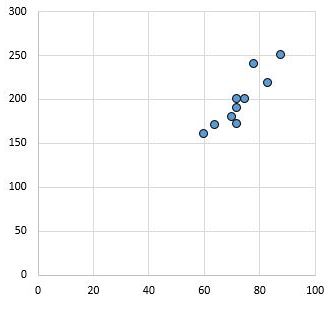
Das folgende Streudiagramm zeigt beispielsweise die Werte zweier Variablen mit einem Korrelationskoeffizienten von r = 0,94.
Dieser Wert ist weit von Null entfernt, was darauf hindeutet, dass zwischen den beiden Variablen eine starke positive Beziehung besteht.
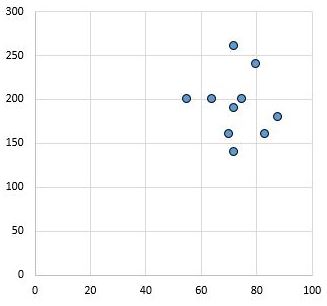
Umgekehrt zeigt das folgende Streudiagramm die Werte zweier Variablen, die einen Korrelationskoeffizienten von r = 0,03 haben. Dieser Wert liegt nahe bei Null, was darauf hinweist, dass zwischen den beiden Variablen praktisch keine Beziehung besteht.
Im Allgemeinen gilt die Effektgröße als klein, wenn der Wert des Pearson-Korrelationskoeffizienten r etwa 0,1 beträgt, als mittel, wenn r etwa 0,3 beträgt, und als groß, wenn r gleich oder größer als 0,5 ist.
3. Quotenverhältnis
Wenn Sie die Erfolgsaussichten in einer Behandlungsgruppe im Vergleich zu den Erfolgsaussichten in einer Kontrollgruppe untersuchen möchten, ist die häufigste Methode zur Berechnung der Effektgröße die Verwendung des Quotenverhältnisses .
Angenommen, wir haben die folgende Tabelle:
| Effektgröße | #Erfolg | #Schach |
|---|---|---|
| Behandlungsgruppe | HAT | B |
| Kontrollgruppe | VS | D |
Das Quotenverhältnis würde wie folgt berechnet:
Quotenverhältnis = (AD) / (BC)
Je weiter das Odds Ratio von 1 entfernt ist, desto höher ist die Wahrscheinlichkeit, dass die Behandlung einen echten Effekt hervorruft.
Die Vorteile der Verwendung von Effektgrößen gegenüber P-Werten
Effektgrößen haben gegenüber p-Werten mehrere Vorteile:
1. Eine Effektgröße hilft uns, eine bessere Vorstellung davon zu bekommen, wie groß der Unterschied zwischen zwei Gruppen ist oder wie stark der Zusammenhang zwischen zwei Gruppen ist. Ein p-Wert kann uns nur sagen, ob ein signifikanter Unterschied oder ein signifikanter Zusammenhang besteht .
2. Im Gegensatz zu p-Werten können Effektgrößen verwendet werden, um die Ergebnisse verschiedener Studien, die in verschiedenen Umgebungen durchgeführt wurden, quantitativ zu vergleichen. Aus diesem Grund werden in Metaanalysen häufig Effektgrößen verwendet.
3. P-Werte können durch große Stichprobengrößen beeinflusst werden. Je größer die Stichprobe, desto größer ist die statistische Aussagekraft eines Hypothesentests, sodass auch kleine Effekte erkannt werden können. Dies kann trotz kleiner Effektgrößen, die möglicherweise keine praktische Bedeutung haben, zu niedrigen p-Werten führen.
Ein einfaches Beispiel kann dies deutlich veranschaulichen: Angenommen, wir möchten wissen, ob zwei Lerntechniken zu unterschiedlichen Testergebnissen führen. Wir haben eine Gruppe von 20 Studenten, die eine Lerntechnik verwenden, während eine andere Gruppe von 20 Studenten eine andere Lerntechnik verwendet. Anschließend geben wir jedem Schüler den gleichen Test.
Die durchschnittliche Punktzahl der Gruppe 1 beträgt 90,65 und die durchschnittliche Punktzahl der Gruppe 2 beträgt 90,75 . Die Standardabweichung für Probe 1 beträgt 2,77 und die Standardabweichung für Probe 2 beträgt 2,78 .
Wenn wir einen unabhängigen t-Test bei zwei Stichproben durchführen, stellt sich heraus, dass die Teststatistik -0,113 und der entsprechende p-Wert 0,91 beträgt. Der Unterschied zwischen den durchschnittlichen Testergebnissen ist statistisch nicht signifikant.
Bedenken Sie jedoch, dass die Stichprobengrößen beider Stichproben jeweils 200 betragen, die Mittelwerte und Standardabweichungen jedoch genau gleich bleiben.
In diesem Fall würde ein unabhängiger t-Test bei zwei Stichproben ergeben, dass die Teststatistik -1,97 beträgt und der entsprechende p-Wert knapp unter 0,05 liegt. Der Unterschied zwischen den durchschnittlichen Testergebnissen ist statistisch signifikant.
Der zugrunde liegende Grund, warum große Stichprobengrößen zu statistisch signifikanten Schlussfolgerungen führen können, liegt in der Formel, die zur Berechnung der T- Test-Statistiken verwendet wird:
Teststatistik t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
Beachten Sie, dass der ganzzahlige Nenner der t -Test-Statistik klein ist, wenn n 1 und n 2 klein sind. Und wenn man durch eine kleine Zahl dividiert, erhält man eine große Zahl. Dies bedeutet, dass die t- Test-Statistik groß und der entsprechende p-Wert klein ist, was zu statistisch signifikanten Ergebnissen führt.
Was gilt als gute Effektgröße?
Eine von Studierenden häufig gestellte Frage lautet: Was gilt als gute Effektgröße?
Die kurze Antwort: Eine Effektgröße kann nicht „gut“ oder „schlecht“ sein, da sie lediglich die Größe des Unterschieds zwischen zwei Gruppen oder die Stärke der Assoziation zwischen zwei Gruppen misst.
Allerdings können wir die folgenden Faustregeln verwenden, um zu quantifizieren, ob das Ausmaß eines Effekts klein, mittel oder groß ist:
Cohens D:
- Ein d von 0,2 oder weniger gilt als kleine Effektgröße.
- Ein d von 0,5 gilt als mittlere Effektgröße.
- Ein d von 0,8 oder mehr gilt als große Effektgröße.
Pearson-Korrelationskoeffizient
- Ein absoluter Wert von r um 0,1 gilt als kleine Effektgröße.
- Ein absoluter Wert von r um 0,3 gilt als mittlere Effektgröße.
- Ein absoluter Wert von r größer als 0,5 wird als große Effektgröße angesehen.
Die Definition einer „starken“ Korrelation kann jedoch von Feld zu Feld unterschiedlich sein. Lesen Sie diesen Artikel, um besser zu verstehen, was als starke Korrelation zwischen verschiedenen Branchen gilt.