So führen sie einen t-test bei einer stichprobe in spss durch

Ein T-Test bei einer Stichprobe wird verwendet, um zu testen, ob der Mittelwert einer Grundgesamtheit einem bestimmten Wert entspricht oder nicht.

In diesem Tutorial wird erläutert, wie Sie in SPSS einen T-Test bei einer Stichprobe durchführen.

Beispiel: T-Test bei einer Stichprobe in SPSS

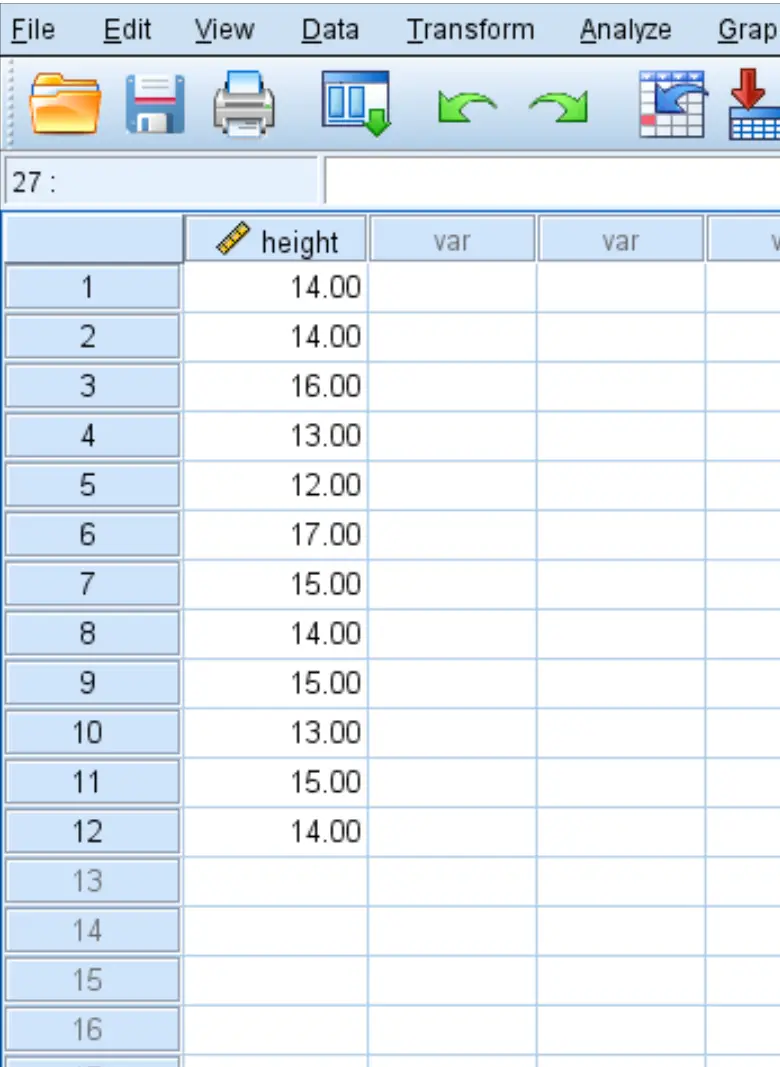
Ein Botaniker möchte wissen, ob die durchschnittliche Höhe einer bestimmten Pflanzenart 15 Zoll beträgt. Sie entnimmt eine Zufallsstichprobe von 12 Pflanzen und notiert jede ihrer Höhen in Zoll:

Verwenden Sie die folgenden Schritte, um einen t-Test bei einer Stichprobe durchzuführen, um zu bestimmen, ob die tatsächliche durchschnittliche Höhe dieser Pflanzenart 15 Zoll beträgt, basierend auf den folgenden Null- und Alternativhypothesen:

• H ₀ : μ = 15 (der reale Bevölkerungsmittelwert beträgt 15 Zoll)
• H ₁ : μ ≠ 15 (der wahre Bevölkerungsmittelwert beträgt nicht 15 Zoll)

Verwenden Sie ein Signifikanzniveau von α = 0,05.

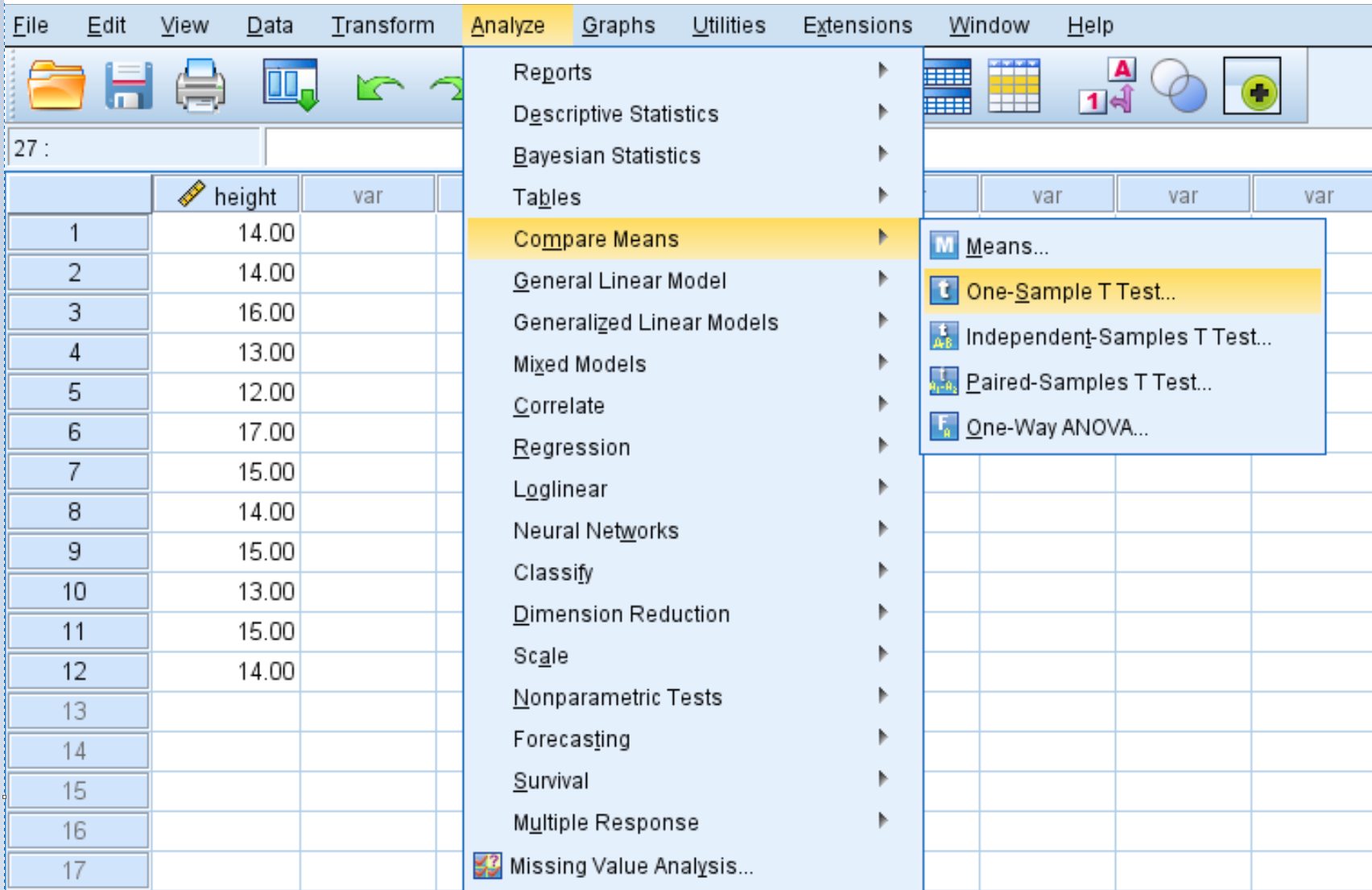
Schritt 1: Wählen Sie die T-Test-Option bei einer Stichprobe.

Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Mittelwerte vergleichen “ und dann auf den T-Test bei einer Stichprobe :

Schritt 2: Geben Sie die Werte ein, die zur Durchführung des T-Tests bei einer Stichprobe erforderlich sind.

Sobald Sie auf One-Sample T Test klicken, erscheint das folgende Fenster:

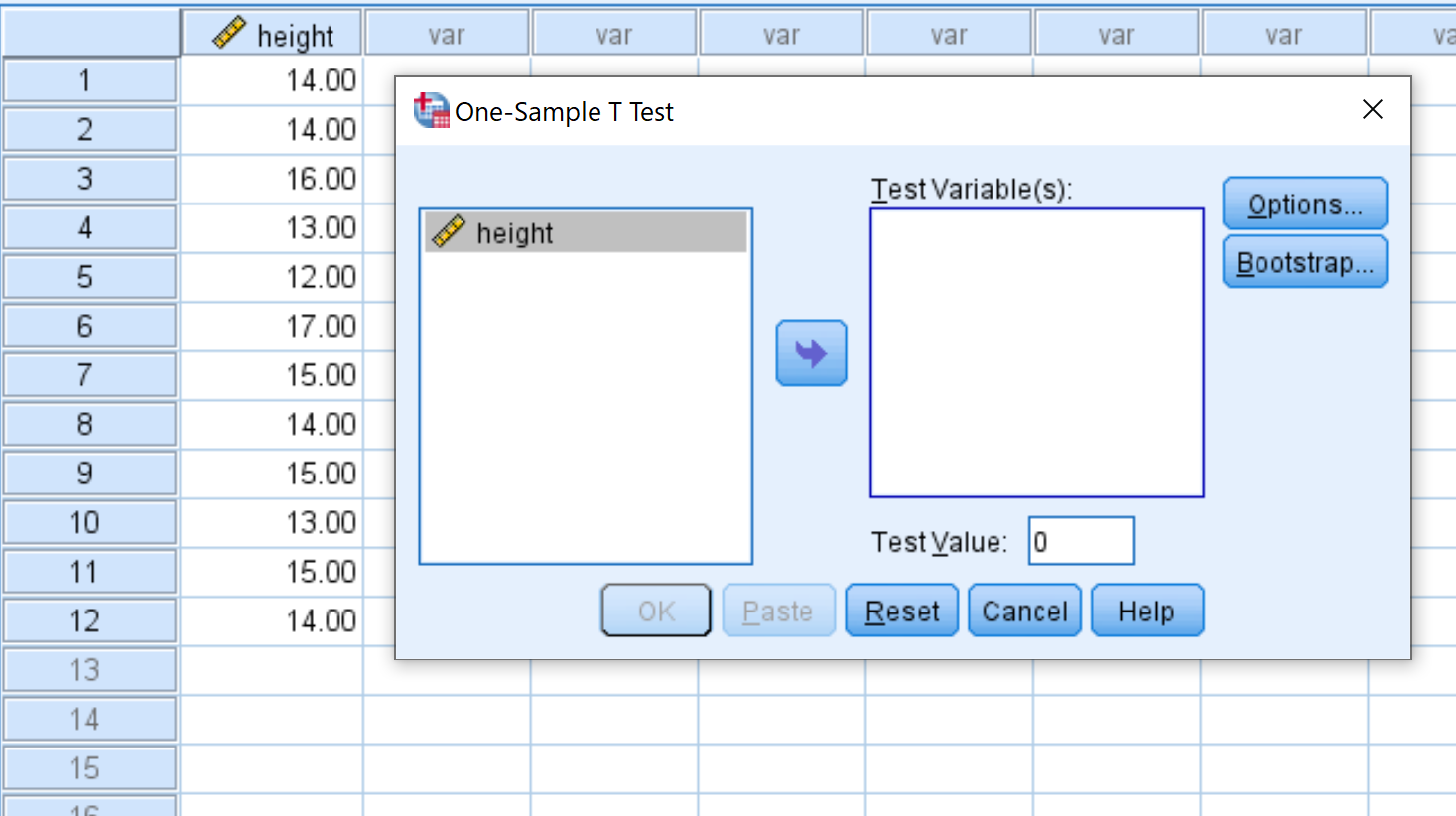
Ziehen Sie die Höhe der Variablen in das Feld mit der Bezeichnung „Testvariable(n)“ und ändern Sie den Testwert auf 15. Klicken Sie dann auf „OK“ .

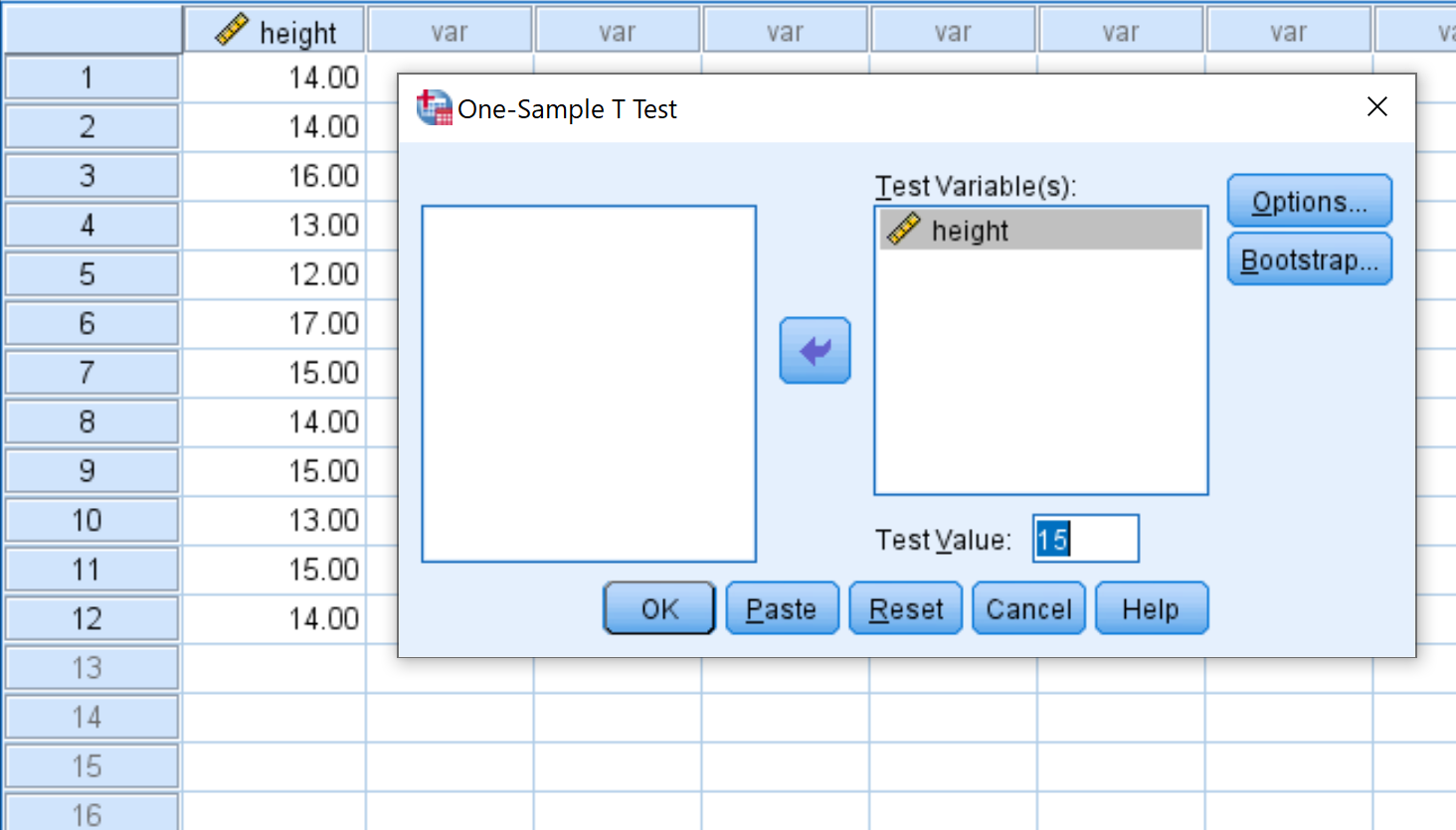
Schritt 3: Interpretieren Sie die Ergebnisse.

Sobald Sie auf „OK“ klicken, werden die Ergebnisse des T-Tests bei einer Stichprobe angezeigt:

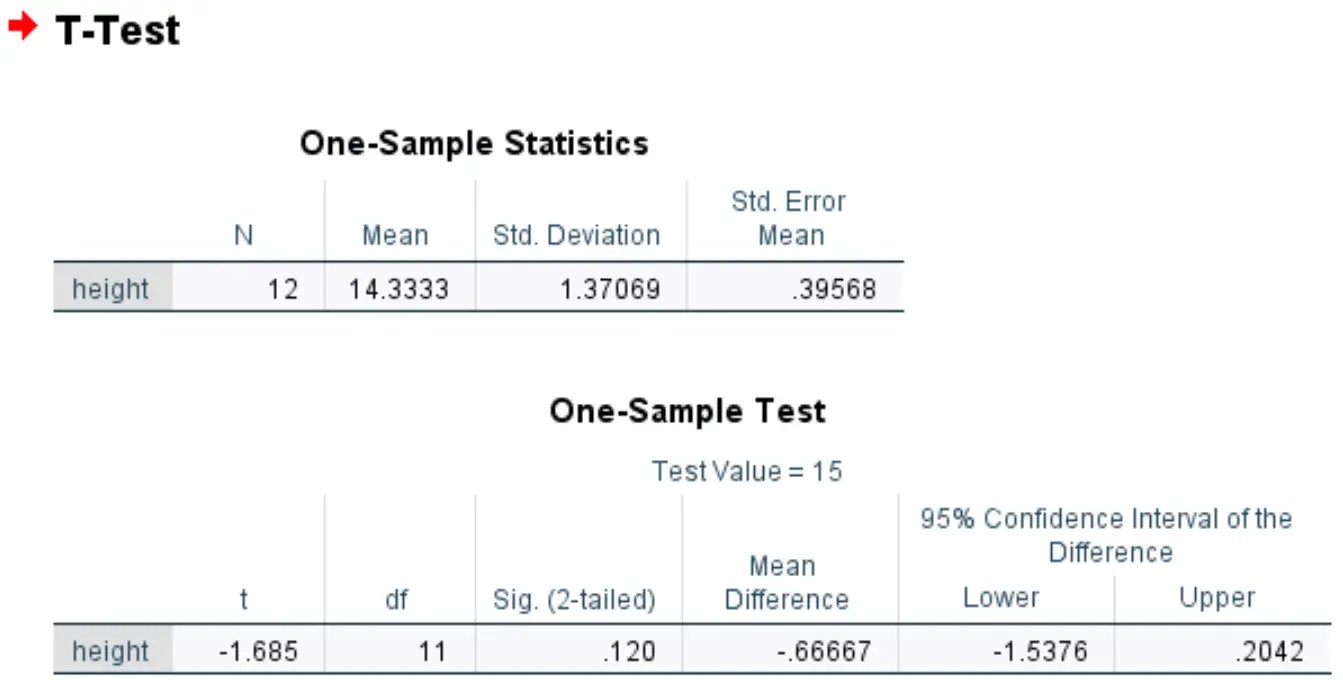
Die erste Tabelle zeigt zusammenfassende Statistiken für variable Höhen:

• N: Stichprobengröße
• Durchschnitt: Die durchschnittliche Höhe der Pflanzen in der Probe
• Standard. Abweichung: Die Standardabweichung der Pflanzenhöhe in der Probe.
• Standard. Mittlerer Fehler: der Standardfehler des Mittelwerts, berechnet als s/√n

Die zweite Tabelle zeigt die Ergebnisse des T-Tests bei einer Stichprobe:

• t: Die Teststatistik, berechnet als (x – μ) / (s/√n) = (14,3333-15) / (1,37/√12) = -1,685
• df: Die Freiheitsgrade, berechnet als n-1 = 12-1 = 11
• Sig. (zweiseitig): Der zweiseitige p-Wert, der einem Wert von -1,685 mit df=11 entspricht
• Mittelwertdifferenz: die Differenz zwischen dem Stichprobenmittelwert und dem hypothetischen Mittelwert
• 95 %-KI der Differenz: 95 % -Konfidenzintervall für die wahre Differenz zwischen dem Stichprobenmittelwert und dem hypothetischen Mittelwert.

Da der p-Wert des Tests (0,120) nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Wir haben nicht genügend Beweise, um sagen zu können, dass die tatsächliche Durchschnittshöhe dieser Pflanzenart etwas anderes als 15 Zoll beträgt.