Kann ein z-score negativ sein?

In der Statistik sagt uns ein Z-Score , wie viele Standardabweichungen ein Wert vom Mittelwert hat. Wir verwenden die folgende Formel, um einen Z-Score zu berechnen:

z = (X – μ) / σ

Dabei ist X der Wert, den wir analysieren, μ der Mittelwert und σ die Standardabweichung.

Ein Z-Score kann positiv, negativ oder null sein.

Ein positiver Z-Score gibt an, dass ein bestimmter Wert über dem Durchschnitt liegt, ein negativer Z-Score zeigt an, dass ein bestimmter Wert unter dem Durchschnitt liegt, und ein Z-Score von Null zeigt an, dass ein bestimmter Wert dem Durchschnitt entspricht.

Einige Beispiele sollen dies verdeutlichen.

Beispiele: Berechnung eines Z-Scores

Nehmen wir an, wir haben den folgenden Datensatz, der die Höhe (in Zoll) einer bestimmten Pflanzengruppe zeigt:

5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20

Der Stichprobenmittelwert dieses Datensatzes beträgt 13 und die Stichprobenstandardabweichung beträgt 5,51 .

1. Finden Sie den Z-Score für den Wert „8“ in diesem Datensatz.

So berechnen Sie den Z-Score:

z = (X – μ) / σ = (8 – 13) / 5,51 = -0,91

Das bedeutet, dass der Wert „8“ 0,91 Standardabweichungen niedriger ist als der Mittelwert.

2. Finden Sie den Z-Score für den Wert „13“ in diesem Datensatz.

So berechnen Sie den Z-Score:

z = (X – μ) / σ = (13 – 13) / 5,46 = 0

Das bedeutet, dass der Wert „13“ genau dem Durchschnitt entspricht.

3. Finden Sie den Z-Score für den Wert „20“ in diesem Datensatz.

So berechnen Sie den Z-Score:

z = (X – μ) / σ = (20 – 13) / 5,46 = 1,28

Das bedeutet, dass der Wert „20“ 1,28 Standardabweichungen über dem Mittelwert liegt.

So interpretieren Sie Z-Scores

Das AZ-Diagramm zeigt uns, wie viel Prozent der Werte unter bestimmte Z-Werte fallen. Einige Beispiele sollen dies verdeutlichen.

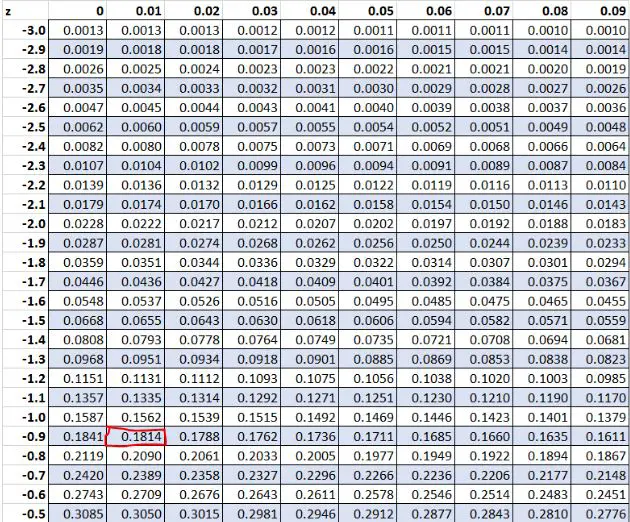
Beispiel 1: Negative Z-Scores

Zuvor haben wir festgestellt, dass der Rohwert „8“ in unserem Datensatz einen Z-Score von -0,91 hatte. Laut Z-Tabelle liegen 18,14 % der Werte unter diesem Wert.

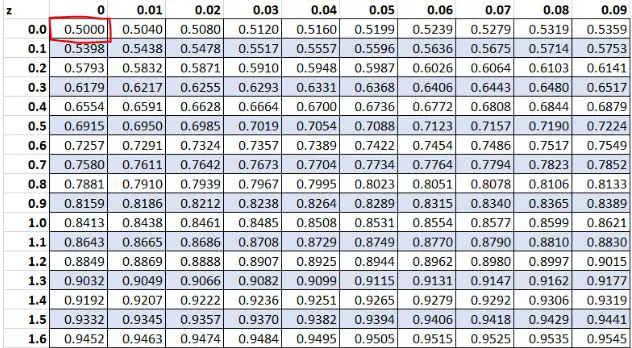
Beispiel 2: Z-Scores gleich Null

Zuvor haben wir festgestellt, dass der Rohwert „13“ in unserem Datensatz einen Z-Score von 0 hatte. Laut Z-Tabelle liegen 50,00 % der Werte unter diesem Wert.

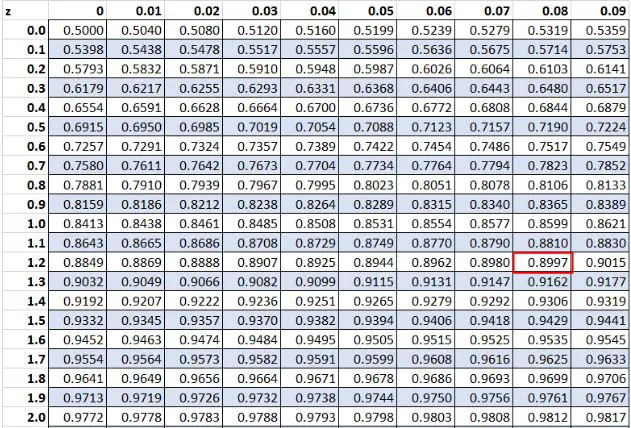
Beispiel 3: Positive Z-Werte

Zuvor haben wir festgestellt, dass der Rohwert „20“ in unserem Datensatz einen Z-Score von 1,28 hatte. Laut Z-Tabelle liegen 89,97 % der Werte unter diesem Wert.

Abschluss

Z-Scores können jeden Wert zwischen negativer Unendlichkeit und positiver Unendlichkeit annehmen, aber die meisten Z-Scores liegen innerhalb von 2 Standardabweichungen vom Mittelwert. In der Statistik gibt es tatsächlich eine Faustregel , die besagt, dass für einen gegebenen Datensatz mit einer Normalverteilung gilt:

• 68 % der Datenwerte liegen innerhalb einer Standardabweichung vom Mittelwert.
• 95 % der Datenwerte liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
• 99,7 % der Datenwerte liegen innerhalb von drei Standardabweichungen vom Mittelwert.

Je höher der absolute Wert eines Z-Scores ist, desto weiter entfernt ist ein Rohwert vom Mittelwert des Datensatzes. Je niedriger der absolute Wert eines Z-Scores ist, desto näher liegt ein Rohwert am Mittelwert des Datensatzes.

Verwandte Themen:

Faustregelrechner
So wenden Sie die Faustregel in Excel an