So verwenden sie qq-plots zur überprüfung der normalität

Ein QQ-Plot, kurz für „Quantil-Quantil“, wird verwendet, um zu bewerten, ob ein Datensatz möglicherweise aus einer theoretischen Verteilung stammt.

In den meisten Fällen wird dieser Diagrammtyp verwendet, um zu bestimmen, ob ein Datensatz einer Normalverteilung folgt oder nicht.

Wenn die Daten normalverteilt sind, liegen die Punkte in einem QQ-Diagramm auf einer geraden diagonalen Linie.

Umgekehrt gilt: Je stärker die Punkte im Diagramm von einer geraden Diagonale abweichen, desto unwahrscheinlicher ist es, dass der Datensatz einer Normalverteilung folgt.

Die folgenden Beispiele zeigen, wie man QQ-Diagramme in R erstellt, um die Normalität zu überprüfen.

Beispiel 1: QQ-Diagramm für normale Daten

Der folgende Code zeigt, wie man einen normalverteilten Datensatz mit 200 Beobachtungen generiert und ein QQ-Diagramm für den Datensatz in R erstellt:

 #make this example reproducible
set. seeds (1)

#create some fake data that follows a normal distribution
data <- rnorm(200)

#create QQ plot
qqnorm(data)
qqline(data)

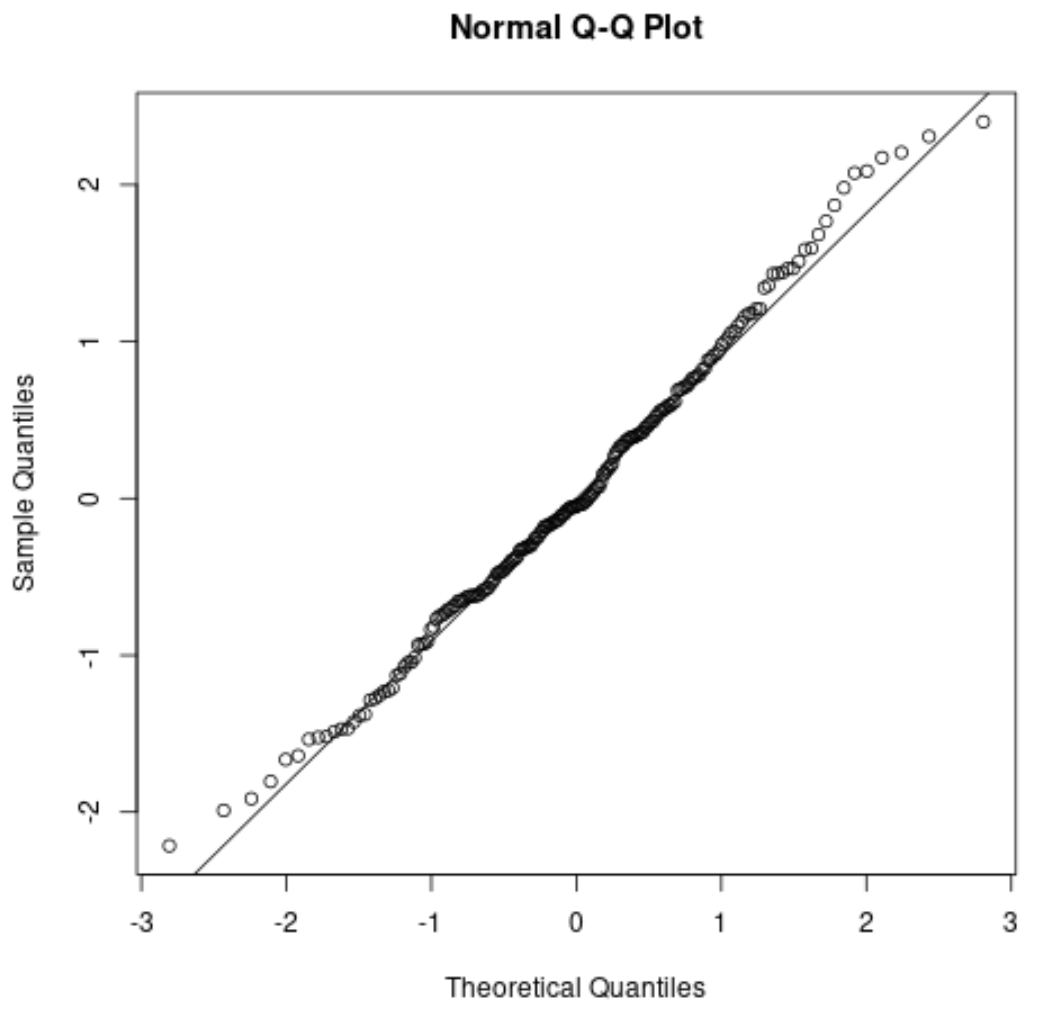
Wir können sehen, dass die Punkte hauptsächlich entlang der geraden diagonalen Linie liegen, mit einigen geringfügigen Abweichungen entlang der einzelnen Enden.

Basierend auf dieser Grafik können wir mit Sicherheit davon ausgehen, dass dieser Datensatz normalverteilt ist.

Beispiel 2: QQ-Diagramm für nicht normale Daten

Der folgende Code zeigt, wie ein QQ-Diagramm für einen Datensatz erstellt wird, der einer Exponentialverteilung mit 200 Beobachtungen folgt:

 #make this example reproducible
set. seeds (1)

#create some fake data that follows an exponential distribution
data <- rexp(200, rate=3)

#create QQ plot
qqnorm(data)
qqline(data)

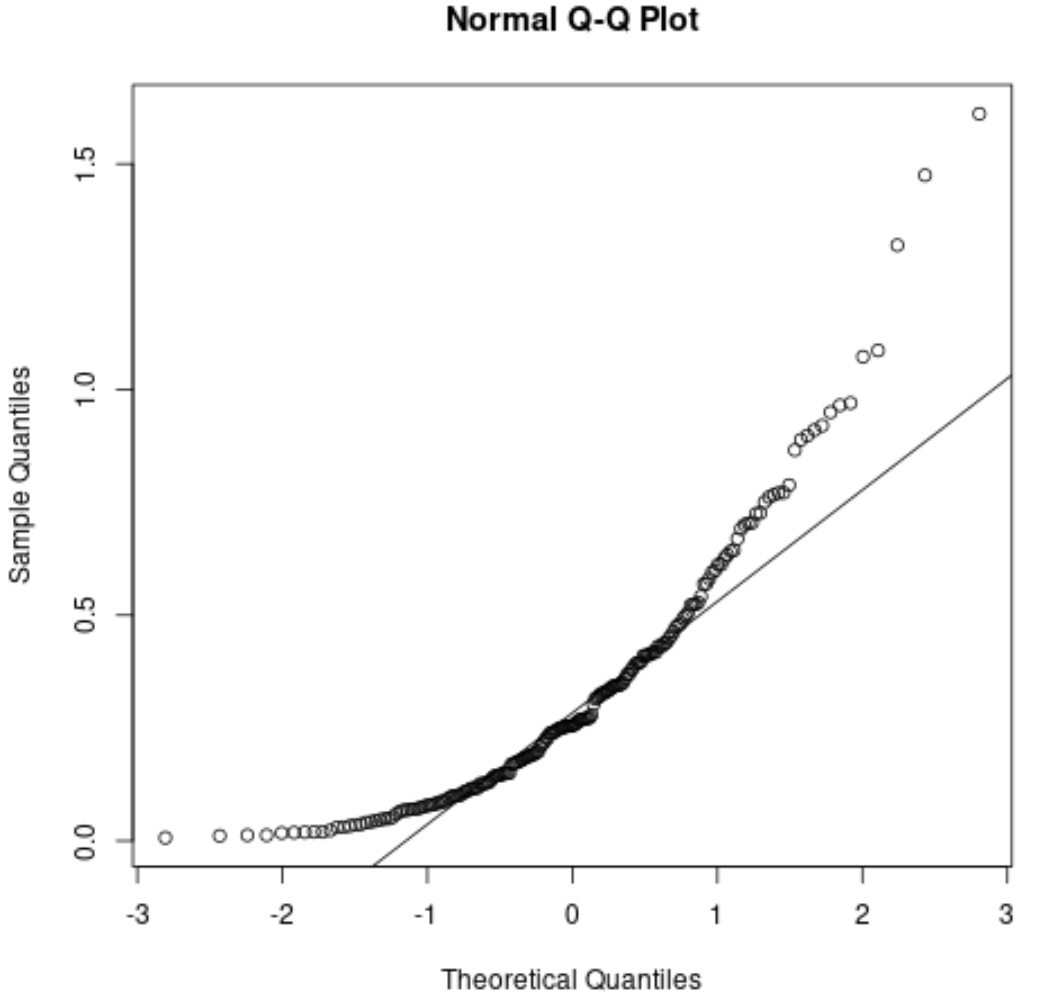
Wir sehen, dass die Punkte erheblich von der Diagonalen abweichen. Dies zeigt deutlich, dass der Datensatz nicht normalverteilt ist.

Dies sollte sinnvoll sein, da wir angegeben haben, dass die Daten einer Exponentialverteilung folgen sollen.

QQ-Diagramme und Histogramme

Es ist zu beachten, dass QQ-Plots eine Möglichkeit sind, visuell zu überprüfen, ob ein Datensatz einer Normalverteilung folgt oder nicht.

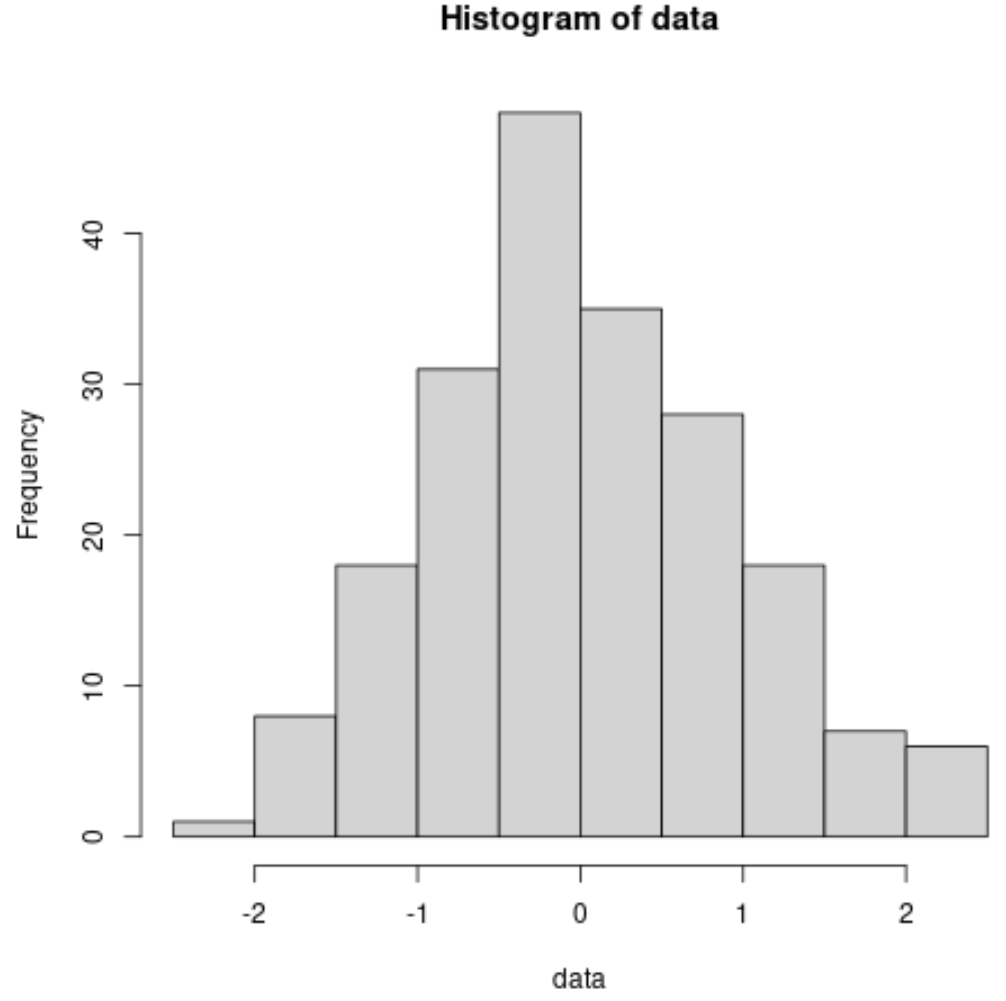
Eine andere Möglichkeit, die Normalität visuell zu überprüfen, besteht darin, ein Histogramm des Datensatzes zu erstellen. Wenn die Daten im Histogramm ungefähr einer Glockenkurve folgen, können wir davon ausgehen, dass der Datensatz normalverteilt ist.

So erstellen Sie beispielsweise ein Histogramm für den zuvor normalverteilten Datensatz:

 #make this example reproducible
set. seeds (1)

#create some fake data that follows a normal distribution
data <- rnorm(200)

#create a histogram to visualize the distribution
hist(data) 

Und so erstellen Sie ein Histogramm für den Datensatz, der einer exponentiellen Prior-Verteilung folgt:

 #make this example reproducible
set. seeds (1)

#create some fake data that follows an exponential distribution
data <- rexp(200, rate=3)

#create a histogram to visualize the distribution
hist(data) 

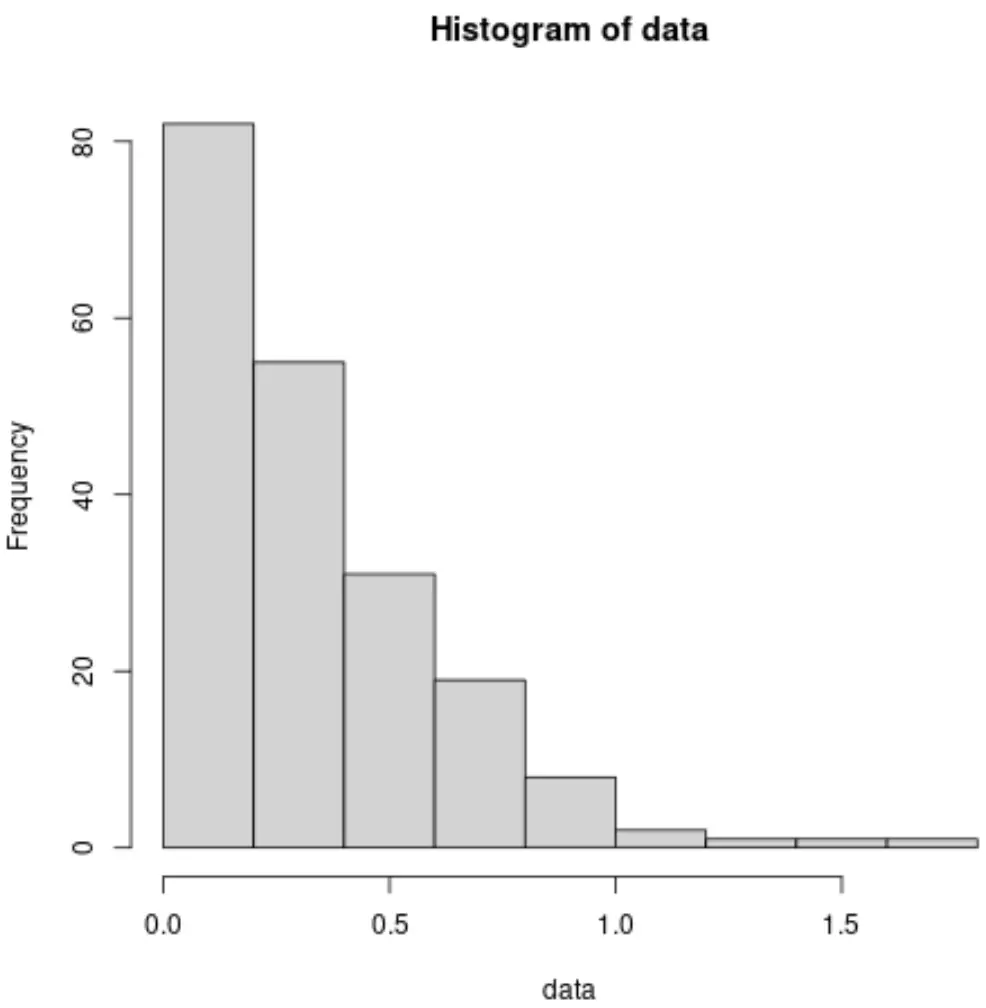
Wir sehen, dass das Histogramm überhaupt nicht wie eine Glockenkurve aussieht, was deutlich darauf hinweist, dass die Daten keiner Normalverteilung folgen.

Zusätzliche Ressourcen

Was ist die Normalitätsannahme in der Statistik?
So erstellen Sie ein QQ-Diagramm in R
So erstellen Sie ein QQ-Diagramm in Excel
So erstellen Sie ein QQ-Diagramm in Python