Einfache lineare regression

In diesem Artikel wird erklärt, was eine einfache lineare Regression in der Statistik ist und wie sie durchgeführt wird. Ebenso finden Sie online eine einfache lineare Regressionsübung gelöst und zusätzlich einen einfachen linearen Regressionsrechner.

Was ist eine einfache lineare Regression?

Die einfache lineare Regression ist ein statistisches Modell, mit dem eine unabhängige Variable in Beziehung gesetzt wird, und wir versuchen, die Beziehung zwischen den beiden Variablen anzunähern.

Daher wird eine einfache lineare Regression verwendet, um eine Gleichung zu finden, die zwei Variablen linear in Beziehung setzt. Logischerweise muss die Beziehung zwischen den beiden Variablen linear sein, andernfalls muss ein anderes Regressionsmodell verwendet werden.

Die Gleichung eines einfachen linearen Regressionsmodells besteht aus zwei Koeffizienten: der Konstante der Gleichung (b ₀ ) und dem Korrelationskoeffizienten zwischen den beiden Variablen (b ₁ ). Daher lautet die Gleichung für ein einfaches lineares Regressionsmodell y=b ₀ +b ₁ x.

Die Gleichung für eine einfache lineare Regression wird als gerade Linie dargestellt, sodass der Koeffizient b ₀ der Achsenabschnitt und der Koeffizient b ₁ die Steigung der Linie ist.

Einfache lineare Regressionsformeln

Die Formeln zur Berechnung der Koeffizienten einer einfachen linearen Regression lauten wie folgt:

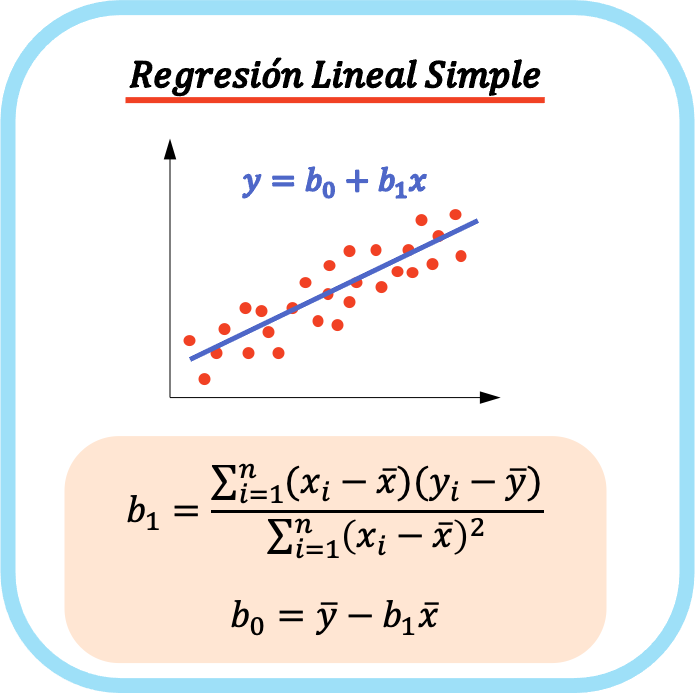
👉 Mit dem Rechner unten können Sie die Koeffizienten einer einfachen linearen Regression für jeden Datensatz berechnen.

Offensichtlich kann die aus dem einfachen linearen Regressionsmodell resultierende Gleichung nicht den genauen Wert aller Beobachtungen erraten, da dieses Modell lediglich versucht, eine Gleichung zu finden, die die Beziehung zwischen den beiden Variablen annähert. Somit ist das Residuum als Differenz zwischen dem wahren Wert und dem durch das lineare Regressionsmodell geschätzten Wert definiert.

Beachten Sie, dass das Ziel eines einfachen linearen Regressionsmodells darin besteht, die Quadrate der Residuen zu minimieren, d. h. eine einfache lineare Regression basiert auf dem Kriterium der kleinsten Quadrate .

Konkretes Beispiel einer einfachen linearen Regression

Um das Verständnis der einfachen linearen Regressionsmethode zu vervollständigen, finden Sie hier ein praktisches Schritt-für-Schritt-Beispiel, in dem die Gleichung eines einfachen linearen Regressionsmodells aus einem Satz statistischer Daten berechnet wird.

• Nach einer Statistikprüfung wurden fünf Studenten gefragt, wie viele Stunden sie für die Prüfung aufgewendet hatten. Die Daten sind in der folgenden Tabelle aufgeführt. Führen Sie ein einfaches lineares Regressionsmodell der gesammelten statistischen Daten durch, um die Lernstunden linear mit der erreichten Note in Beziehung zu setzen.

Um ein einfaches lineares Regressionsmodell durchzuführen, müssen wir die Koeffizienten b ₀ und b ₁ der Gleichung bestimmen und dafür die Formeln aus dem obigen Abschnitt verwenden.

Um jedoch die einfachen linearen Regressionsformeln anzuwenden, müssen wir zunächst den Mittelwert der unabhängigen Variablen und den Mittelwert der abhängigen Variablen berechnen:

Nachdem wir nun die Mittelwerte der Variablen kennen, berechnen wir den Koeffizienten b ₁ des Modells mithilfe der entsprechenden Formel:

Schließlich berechnen wir den Koeffizienten b ₀ des Modells mithilfe der entsprechenden Formel:

Kurz gesagt lautet die Gleichung für das einfache lineare Regressionsmodell des Problems:

Unten sehen Sie die grafische Darstellung der Beispieldaten sowie die Gerade des einfachen linearen Regressionsmodells:

Nachdem wir schließlich die Gleichung des einfachen linearen Regressionsmodells berechnet haben, müssen wir nur noch das erhaltene Ergebnis interpretieren. Hierzu ist es unerlässlich, das Bestimmtheitsmaß des Regressionsmodells zu berechnen, wie das geht, können Sie nachschauen, indem Sie auf unserer Website nach dem entsprechenden Artikel suchen.

Einfache lineare Regressionsannahmen

Um eine einfache lineare Regression durchzuführen, müssen die folgenden Annahmen erfüllt sein:

• Unabhängigkeit : Die beobachteten Reste müssen unabhängig voneinander sein. Eine gängige Methode zur Sicherstellung der Modellunabhängigkeit besteht darin, dem Stichprobenverfahren Zufälligkeit hinzuzufügen.
• Homoskedastizität : Die Varianzen der Residuen müssen homogen sein, d. h. die Variabilität der Residuen muss konstant sein.
• Normalität : Die Residuen müssen normalverteilt sein, d. h. sie müssen einer Normalverteilung mit einem Mittelwert von 0 folgen.
• Linearität – Die Beziehung zwischen der unabhängigen Variablen und der abhängigen Variablen sollte linear sein.

Einfacher linearer Regressionsrechner

Geben Sie Beispieldaten in den Rechner unten ein, um ein einfaches lineares Regressionsmodell zwischen zwei Variablen anzupassen. Sie müssen die Datenpaare trennen, sodass im ersten Feld nur die Werte der unabhängigen Variablen X und im zweiten Feld nur die Werte der abhängigen Variablen Y stehen.

Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Einfache und multiple lineare Regression

Abschließend werden wir sehen, was der Unterschied zwischen der einfachen linearen Regression und der multiplen linearen Regression ist, da es sich um zwei Arten linearer Regressionen handelt, die in der Statistik häufig verwendet werden.

Die multiple lineare Regression ermöglicht es, zwei oder mehr erklärende Variablen mathematisch mit einer Antwortvariablen zu verknüpfen. Das heißt, bei der multiplen linearen Regression wird ein Modell erstellt, in dem es mindestens zwei unabhängige Variablen gibt.

Daher besteht der Unterschied zwischen einfacher linearer Regression und multipler linearer Regression in der Anzahl unabhängiger Variablen. Bei der einfachen linearen Regression gibt es nur eine unabhängige Variable, während es bei der multiplen linearen Regression zwei oder mehr unabhängige Variablen gibt.