So führen sie eine einfache lineare regression in python durch (schritt für schritt)
Die einfache lineare Regression ist eine Technik, mit der wir die Beziehung zwischen einer einzelnen erklärenden Variablen und einer einzelnen Antwortvariablen verstehen können.
Diese Technik findet eine Linie, die am besten zu den Daten „passt“ und hat die folgende Form:
ŷ = b 0 + b 1 x
Gold:
- ŷ : Der geschätzte Antwortwert
- b 0 : Der Ursprung der Regressionslinie
- b 1 : Die Steigung der Regressionsgeraden
Diese Gleichung kann uns helfen, die Beziehung zwischen der erklärenden Variablen und der Antwortvariablen zu verstehen, und (vorausgesetzt, sie ist statistisch signifikant) kann verwendet werden, um den Wert einer Antwortvariablen anhand des Werts der erklärenden Variablen vorherzusagen.
Dieses Tutorial bietet eine Schritt-für-Schritt-Erklärung zur Durchführung einer einfachen linearen Regression in Python.
Schritt 1: Daten laden
Für dieses Beispiel erstellen wir einen gefälschten Datensatz mit den folgenden zwei Variablen für 15 Schüler:
- Gesamtzahl der Stunden, die für bestimmte Prüfungen gelernt wurden
- Prüfungsergebnis
Wir werden versuchen, ein einfaches lineares Regressionsmodell anzupassen, das Stunden als erklärende Variable und Untersuchungsergebnisse als Antwortvariable verwendet.
Der folgende Code zeigt, wie dieser gefälschte Datensatz in Python erstellt wird:
import pandas as pd #create dataset df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14], ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]}) #view first six rows of dataset df[0:6] hours score 0 1 64 1 2 66 2 4 76 3 5 73 4 5 74 5 6 81
Schritt 2: Visualisieren Sie die Daten
Bevor wir ein einfaches lineares Regressionsmodell anpassen, müssen wir zunächst die Daten visualisieren, um sie zu verstehen.
Zunächst möchten wir sicherstellen, dass die Beziehung zwischen Stunden und Punktzahl annähernd linear ist, da dies eine zugrunde liegende Annahme einer einfachen linearen Regression ist.
Wir können ein einfaches Streudiagramm erstellen, um die Beziehung zwischen den beiden Variablen zu visualisieren:
import matplotlib.pyplot as plt plt. scatter (df.hours, df.score) plt. title (' Hours studied vs. Exam Score ') plt. xlabel (' Hours ') plt. ylabel (' Score ') plt. show ()
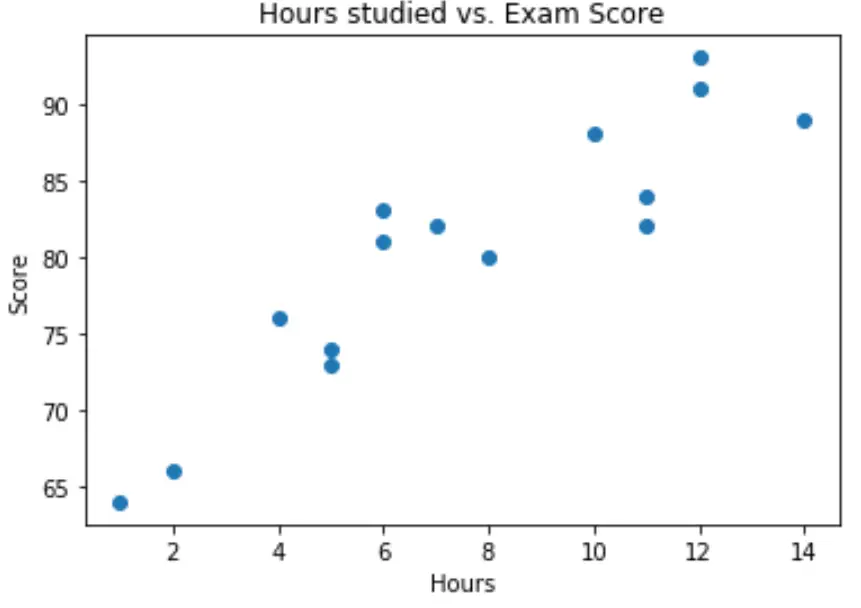
Aus der Grafik können wir ersehen, dass die Beziehung linear zu sein scheint. Mit zunehmender Stundenzahl steigt tendenziell auch die Punktzahl linear an.
Anschließend können wir ein Boxplot erstellen, um die Verteilung der Prüfungsergebnisse zu visualisieren und auf Ausreißer zu prüfen. Standardmäßig definiert Python eine Beobachtung als Ausreißer, wenn sie das 1,5-fache des Interquartilbereichs über dem dritten Quartil (Q3) oder das 1,5-fache des Interquartilbereichs unter dem ersten Quartil (Q1) beträgt.
Wenn eine Beobachtung ein Ausreißer ist, erscheint ein kleiner Kreis im Boxplot:
df. boxplot (column=[' score '])
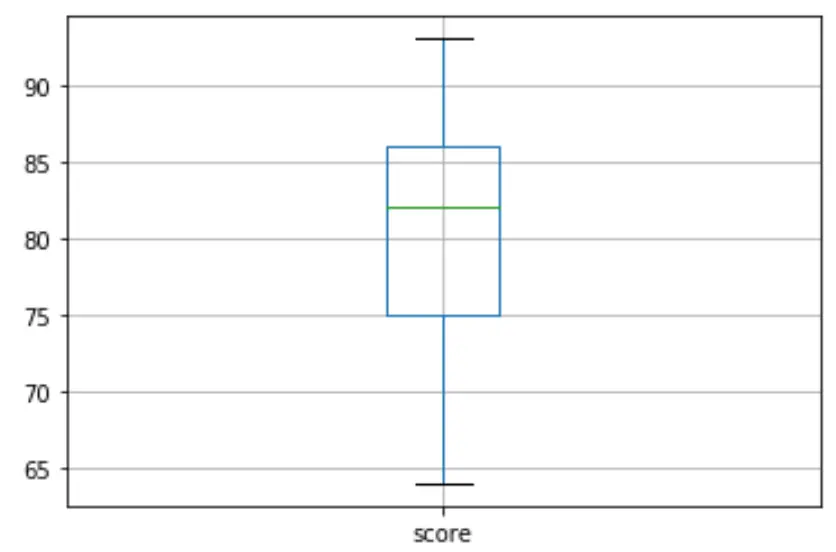
Es gibt keine kleinen Kreise im Boxplot, was bedeutet, dass es in unserem Datensatz keine Ausreißer gibt.
Schritt 3: Führen Sie eine einfache lineare Regression durch
Sobald wir bestätigt haben, dass die Beziehung zwischen unseren Variablen linear ist und es keine Ausreißer gibt, können wir mit der Anpassung eines einfachen linearen Regressionsmodells fortfahren, indem wir Stunden als erklärende Variable und die Punktzahl als Antwortvariable verwenden:
Hinweis: Wir verwenden die Funktion OLS() aus der Statsmodels-Bibliothek, um das Regressionsmodell anzupassen.
import statsmodels.api as sm #define response variable y = df[' score '] #define explanatory variable x = df[[' hours ']] #add constant to predictor variables x = sm. add_constant (x) #fit linear regression model model = sm. OLS (y,x). fit () #view model summary print ( model.summary ()) OLS Regression Results ==================================================== ============================ Dept. Variable: R-squared score: 0.831 Model: OLS Adj. R-squared: 0.818 Method: Least Squares F-statistic: 63.91 Date: Mon, 26 Oct 2020 Prob (F-statistic): 2.25e-06 Time: 15:51:45 Log-Likelihood: -39,594 No. Observations: 15 AIC: 83.19 Df Residuals: 13 BIC: 84.60 Model: 1 Covariance Type: non-robust ==================================================== ============================ coef std err t P>|t| [0.025 0.975] -------------------------------------------------- ---------------------------- const 65.3340 2.106 31.023 0.000 60.784 69.884 hours 1.9824 0.248 7.995 0.000 1.447 2.518 ==================================================== ============================ Omnibus: 4,351 Durbin-Watson: 1,677 Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329 Skew: 0.092 Prob(JB): 0.515 Kurtosis: 1.554 Cond. No. 19.2 ==================================================== ============================
Aus der Modellzusammenfassung können wir ersehen, dass die angepasste Regressionsgleichung lautet:
Punktzahl = 65,334 + 1,9824*(Stunden)
Dies bedeutet, dass jede weitere gelernte Stunde mit einer durchschnittlichen Steigerung der Prüfungspunktzahl um 1,9824 Punkte verbunden ist. Und der ursprüngliche Wert von 65.334 gibt uns die durchschnittlich erwartete Prüfungspunktzahl für einen Studenten an, der null Stunden studiert.
Wir können diese Gleichung auch verwenden, um die erwartete Prüfungspunktzahl basierend auf der Anzahl der Stunden, die ein Student studiert, zu ermitteln. Beispielsweise sollte ein Student, der 10 Stunden lernt, eine Prüfungspunktzahl von 85,158 erreichen:
Punktzahl = 65,334 + 1,9824*(10) = 85,158
So interpretieren Sie den Rest der Modellzusammenfassung:
- P>|t| : Dies ist der p-Wert, der den Modellkoeffizienten zugeordnet ist. Da der p-Wert für Stunden (0,000) deutlich unter 0,05 liegt, können wir sagen, dass ein statistisch signifikanter Zusammenhang zwischen Stunden und Punktzahl besteht.
- R-Quadrat: Diese Zahl sagt uns, dass der Prozentsatz der Variation in den Prüfungsergebnissen durch die Anzahl der gelernten Stunden erklärt werden kann. Im Allgemeinen gilt: Je größer der R-Quadrat-Wert eines Regressionsmodells, desto besser können die erklärenden Variablen den Wert der Antwortvariablen vorhersagen. In diesem Fall werden 83,1 % der Abweichungen in den Ergebnissen durch die untersuchten Stunden erklärt.
- F-Statistik und p-Wert: Die F-Statistik ( 63,91 ) und der entsprechende p-Wert ( 2,25e-06 ) geben Auskunft über die Gesamtbedeutung des Regressionsmodells, d. h. ob die erklärenden Variablen im Modell zur Erklärung der Variation nützlich sind . in der Antwortvariablen. Da der p-Wert in diesem Beispiel weniger als 0,05 beträgt, ist unser Modell statistisch signifikant und Stunden werden als nützlich zur Erklärung der Bewertungsvariation angesehen.
Schritt 4: Erstellen Sie Restdiagramme
Nachdem das einfache lineare Regressionsmodell an die Daten angepasst wurde, besteht der letzte Schritt darin, Residuendiagramme zu erstellen.
Eine der wichtigsten Annahmen der linearen Regression besteht darin, dass die Residuen eines Regressionsmodells annähernd normalverteilt und auf jeder Ebene der erklärenden Variablen homoskedastisch sind. Wenn diese Annahmen nicht erfüllt sind, könnten die Ergebnisse unseres Regressionsmodells irreführend oder unzuverlässig sein.
Um zu überprüfen, ob diese Annahmen erfüllt sind, können wir die folgenden Residuendiagramme erstellen:
Darstellung der Residuen im Vergleich zu angepassten Werten: Diese Darstellung eignet sich zur Bestätigung der Homoskedastizität. Die x-Achse zeigt die angepassten Werte und die y-Achse zeigt die Residuen an. Solange die Residuen scheinbar zufällig und gleichmäßig über den gesamten Graphen um den Nullwert verteilt sind, können wir davon ausgehen, dass die Homoskedastizität nicht verletzt wird:
#define figure size fig = plt. figure (figsize=(12.8)) #produce residual plots fig = sm.graphics. plot_regress_exog (model, ' hours ', fig=fig)
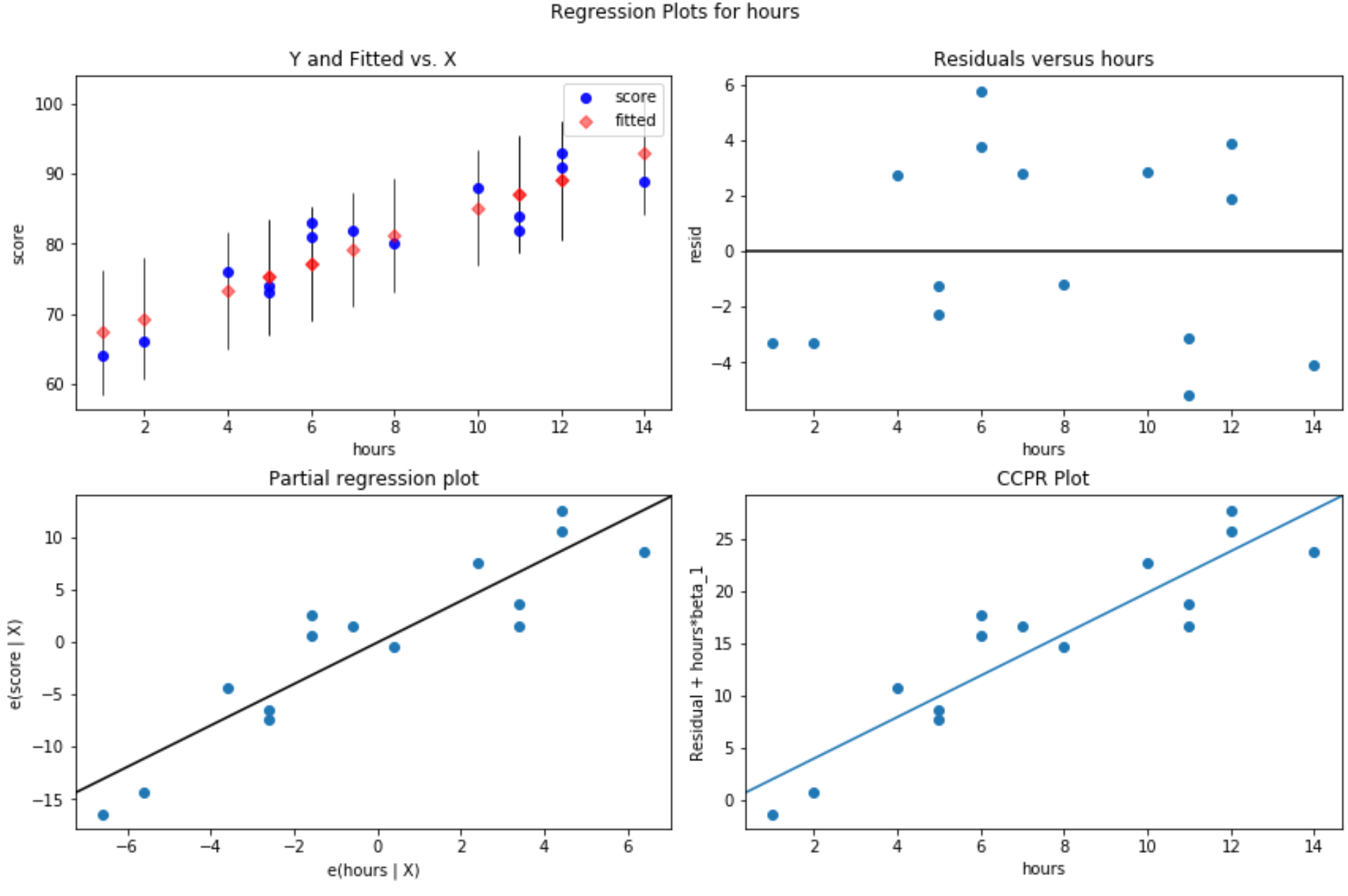
Es entstehen vier Parzellen. Das Bild in der oberen rechten Ecke ist das Residualdiagramm im Vergleich zum angepassten Diagramm. Die x-Achse in diesem Diagramm zeigt die tatsächlichen Werte der Prädiktorvariablenpunkte und die y-Achse zeigt das Residuum für diesen Wert.
Da die Residuen zufällig um den Nullpunkt herum verstreut zu sein scheinen, deutet dies darauf hin, dass Heteroskedastizität bei der erklärenden Variablen kein Problem darstellt.
QQ-Diagramm: Dieses Diagramm ist nützlich, um zu bestimmen, ob die Residuen einer Normalverteilung folgen. Wenn die Datenwerte im Diagramm einer annähernd geraden Linie im 45-Grad-Winkel folgen, sind die Daten normalverteilt:
#define residuals res = model. reside #create QQ plot fig = sm. qqplot (res, fit= True , line=" 45 ") plt.show()
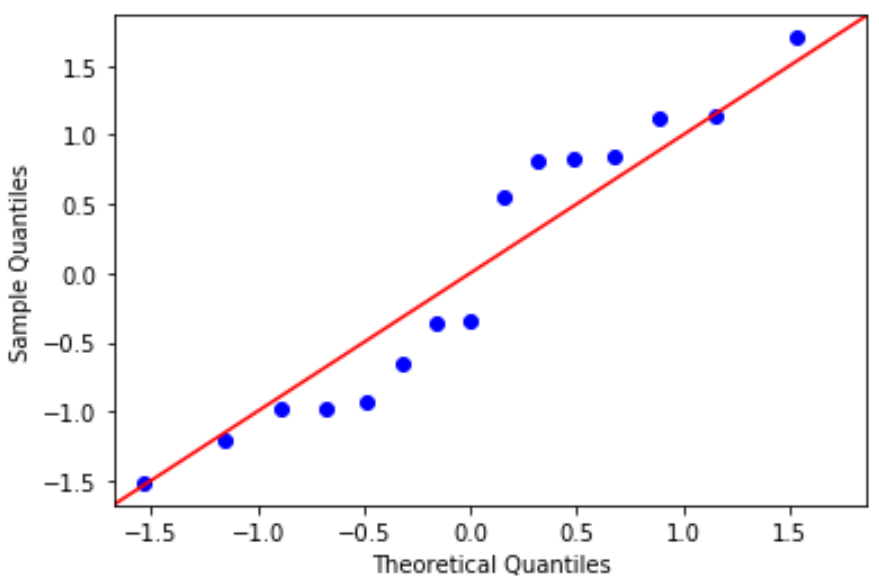
Die Residuen weichen ein wenig von der 45-Grad-Linie ab, aber nicht genug, um ernsthafte Bedenken auszulösen. Wir können davon ausgehen, dass die Normalitätsannahme erfüllt ist.
Da die Residuen normalverteilt und homoskedastisch sind, haben wir überprüft, dass die Annahmen des einfachen linearen Regressionsmodells erfüllt sind. Somit ist die Ausgabe unseres Modells zuverlässig.
Den vollständigen in diesem Tutorial verwendeten Python-Code finden Sie hier .