So führen sie eine einfache lineare regression in sas durch

Die einfache lineare Regression ist eine Technik, mit der wir die Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen verstehen können.

Diese Technik findet eine Linie, die am besten zu den Daten „passt“ und hat die folgende Form:

ŷ = b ₀ + b ₁ x

Gold:

• ŷ : Der geschätzte Antwortwert
• b ₀ : Der Ursprung der Regressionslinie
• b ₁ : Die Steigung der Regressionsgeraden

Diese Gleichung hilft uns, die Beziehung zwischen der Prädiktorvariablen und der Antwortvariablen zu verstehen.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie eine einfache lineare Regression in SAS durchgeführt wird.

Schritt 1: Erstellen Sie die Daten

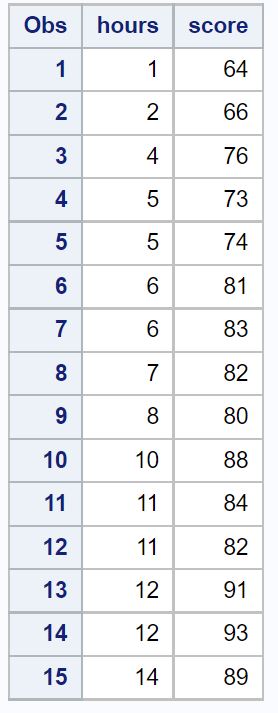
Für dieses Beispiel erstellen wir einen Datensatz, der die Gesamtzahl der gelernten Stunden und die Abschlussprüfungsnote von 15 Studenten enthält.

Wir werden ein einfaches lineares Regressionsmodell anpassen, das Stunden als Prädiktorvariable und den Score als Antwortvariable verwendet.

Der folgende Code zeigt, wie dieser Datensatz in SAS erstellt wird:

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

Schritt 2: Passen Sie das einfache lineare Regressionsmodell an

Als nächstes verwenden wir proc reg, um das einfache lineare Regressionsmodell anzupassen:

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

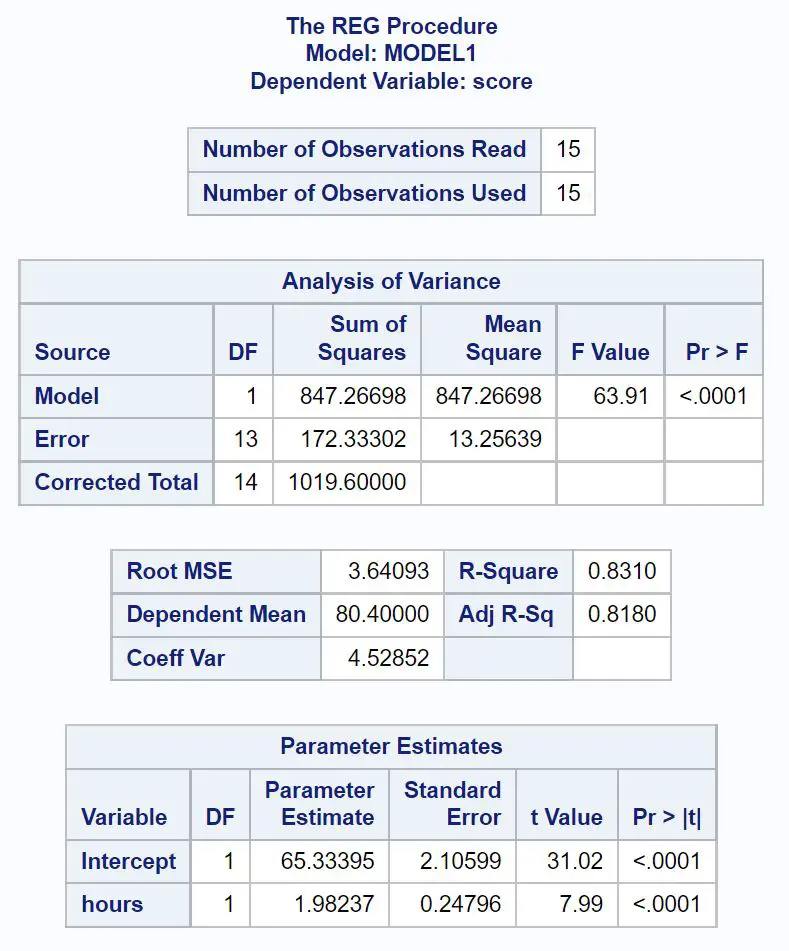
So interpretieren Sie die wichtigsten Werte aus jeder Tabelle im Ergebnis:

Lückenanalysetabelle:

Der Gesamt- F-Wert des Regressionsmodells beträgt 63,91 und der entsprechende p-Wert ist <0,0001 .

Da dieser p-Wert kleiner als 0,05 ist, schließen wir, dass das Regressionsmodell insgesamt statistisch signifikant ist. Mit anderen Worten: Stunden sind eine nützliche Variable zur Vorhersage von Prüfungsergebnissen.

Modellanpassungstabelle:

Der R-Quadrat-Wert gibt uns den Prozentsatz der Variation in den Prüfungsergebnissen an, der durch die Anzahl der gelernten Stunden erklärt werden kann.

Im Allgemeinen gilt: Je größer der R-Quadrat-Wert eines Regressionsmodells, desto besser können die Prädiktorvariablen den Wert der Antwortvariablen vorhersagen.

In diesem Fall können 83,1 % der Abweichungen in den Prüfungsergebnissen durch die Anzahl der gelernten Stunden erklärt werden. Dieser Wert ist ziemlich hoch, was darauf hindeutet, dass die gelernten Stunden eine sehr nützliche Variable für die Vorhersage von Prüfungsergebnissen sind.

Tabelle der Parameterschätzungen:

Aus dieser Tabelle können wir die angepasste Regressionsgleichung sehen:

Punktzahl = 65,33 + 1,98*(Stunden)

Wir interpretieren dies so, dass jede zusätzlich gelernte Stunde mit einer durchschnittlichen Verbesserung der Prüfungspunktzahl um 1,98 Punkte verbunden ist.

Der ursprüngliche Wert besagt, dass die durchschnittliche Prüfungspunktzahl für einen Studenten, der null Stunden studiert, 65,33 beträgt.

Wir können diese Gleichung auch verwenden, um die erwartete Prüfungspunktzahl basierend auf der Anzahl der Stunden, die ein Student studiert, zu ermitteln.

Beispielsweise sollte ein Student, der 10 Stunden lernt, eine Prüfungspunktzahl von 85,13 erreichen:

Punktzahl = 65,33 + 1,98*(10) = 85,13

Da der p-Wert (<0,0001) für Stunden in dieser Tabelle weniger als 0,05 beträgt, schließen wir, dass es sich hierbei um eine statistisch signifikante Prädiktorvariable handelt.

Schritt 3: Residuendiagramme analysieren

Die einfache lineare Regression geht von zwei wichtigen Annahmen über die Modellresiduen aus:

• Die Residuen sind normalverteilt.
• Die Residuen weisen auf jeder Ebene der Prädiktorvariablen die gleiche Varianz („ Homoskedastizität “) auf.

Wenn diese Annahmen nicht erfüllt sind, sind die Ergebnisse unseres Regressionsmodells möglicherweise nicht zuverlässig.

Um zu überprüfen, ob diese Annahmen erfüllt sind, können wir die Residuendiagramme analysieren, die SAS automatisch in der Ausgabe anzeigt:

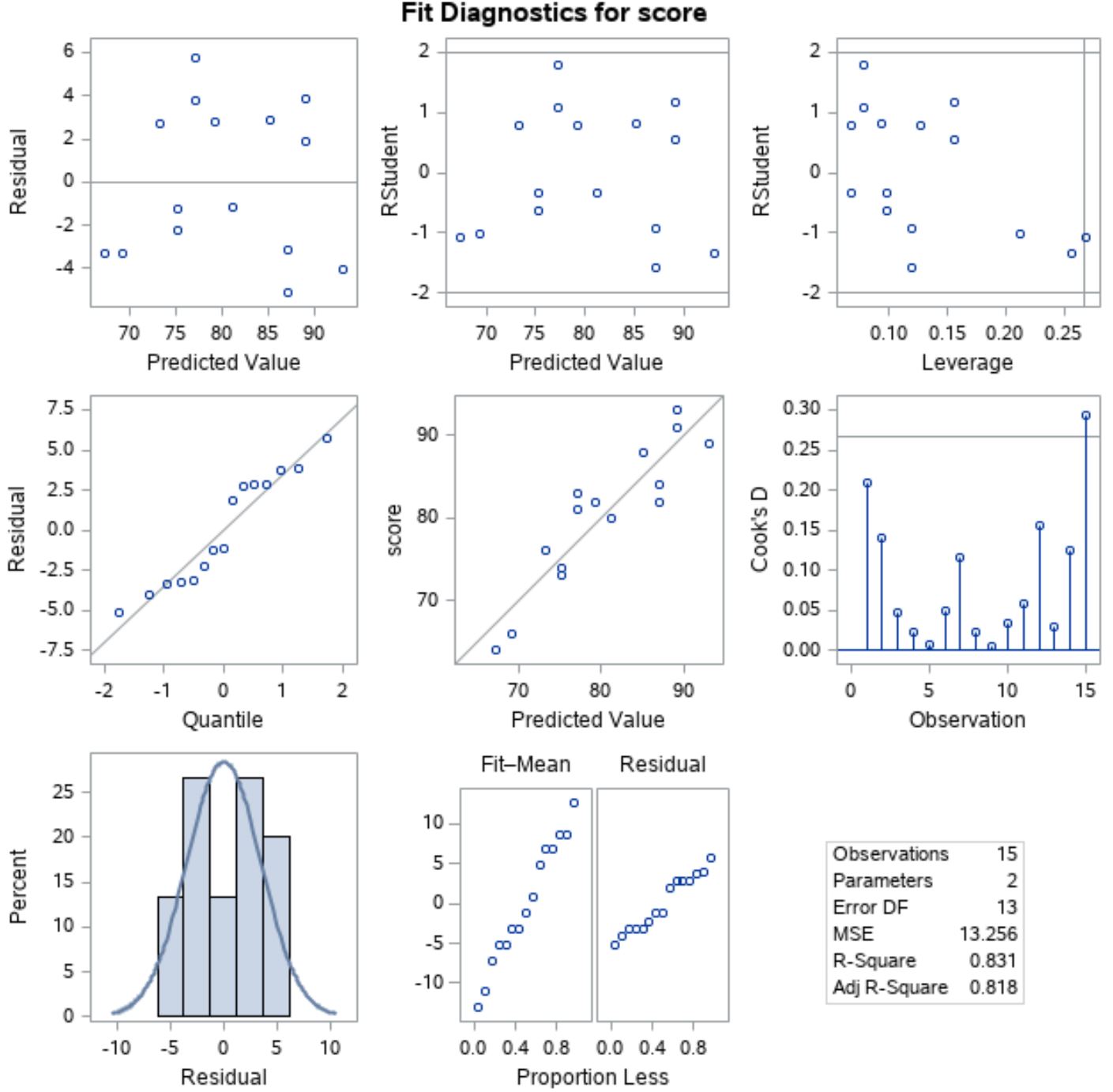
Um zu überprüfen, ob die Residuen normalverteilt sind, können wir das Diagramm an der linken Position der Mittellinie mit „Quantil“ entlang der x-Achse und „Residuum“ entlang der y-Achse analysieren.

Dieses Diagramm wird als QQ-Diagramm bezeichnet, kurz für „Quantil-Quantil“, und wird verwendet, um zu bestimmen, ob die Daten normalverteilt sind oder nicht. Wenn die Daten normalverteilt sind, liegen die Punkte in einem QQ-Diagramm auf einer geraden diagonalen Linie.

Aus der Grafik können wir ersehen, dass die Punkte ungefähr auf einer geraden diagonalen Linie liegen, sodass wir davon ausgehen können, dass die Residuen normalverteilt sind.

Um zu überprüfen, ob die Residuen homoskedastisch sind, können wir uns als Nächstes das Diagramm an der linken Position der ersten Zeile mit „Vorhergesagter Wert“ auf der x-Achse und „Residuum“ auf der y-Achse ansehen.

Wenn die Plotpunkte zufällig um Null herum verstreut sind und kein klares Muster aufweist, können wir davon ausgehen, dass die Residuen homoskedastisch sind.

Aus dem Diagramm können wir ersehen, dass die Punkte zufällig um den Nullpunkt herum verstreut sind und auf jeder Ebene im gesamten Diagramm ungefähr die gleiche Varianz aufweisen. Daher können wir davon ausgehen, dass die Residuen homoskedastisch sind.

Da beide Annahmen erfüllt sind, können wir davon ausgehen, dass die Ergebnisse des einfachen linearen Regressionsmodells zuverlässig sind.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:

So führen Sie eine einfaktorielle ANOVA in SAS durch
So führen Sie eine zweifaktorielle ANOVA in SAS durch
So berechnen Sie die Korrelation in SAS