So führen sie eine einfache lineare regression in stata durch

Die einfache lineare Regression ist eine Methode, mit der Sie die Beziehung zwischen einer erklärenden Variablen x und einer Antwortvariablen y verstehen können.

In diesem Tutorial wird erläutert, wie Sie eine einfache lineare Regression in Stata durchführen.

Beispiel: Einfache lineare Regression in Stata

Angenommen, wir möchten den Zusammenhang zwischen dem Gewicht eines Autos und seinen Meilen pro Gallone verstehen. Um diesen Zusammenhang zu untersuchen, können wir eine einfache lineare Regression durchführen, wobei wir das Gewicht als erklärende Variable und Meilen pro Gallone als Antwortvariable verwenden.

Führen Sie die folgenden Schritte in Stata aus, um eine einfache lineare Regression mit dem Datensatz namens auto durchzuführen, der Daten zu 74 verschiedenen Autos enthält.

Schritt 1: Daten laden.

Laden Sie die Daten, indem Sie Folgendes in das Befehlsfeld eingeben:

Verwenden Sie https://www.stata-press.com/data/r13/auto

Schritt 2: Erhalten Sie eine Datenzusammenfassung.

Verschaffen Sie sich einen schnellen Überblick über die Daten, mit denen Sie arbeiten, indem Sie Folgendes in das Befehlsfeld eingeben:

zusammenfassen

Wir können sehen, dass der Datensatz 12 verschiedene Variablen enthält, aber die einzigen zwei, die uns interessieren, sind mpg und Weight .

Schritt 3: Visualisieren Sie die Daten.

Bevor wir eine einfache lineare Regression durchführen, erstellen wir zunächst ein Streudiagramm des Gewichts im Vergleich zu mpg, damit wir die Beziehung zwischen diesen beiden Variablen visualisieren und nach offensichtlichen Ausreißern suchen können. Geben Sie Folgendes in das Befehlsfeld ein, um ein Streudiagramm zu erstellen:

mpg Gewichtsverteilung

Dadurch entsteht das folgende Streudiagramm:

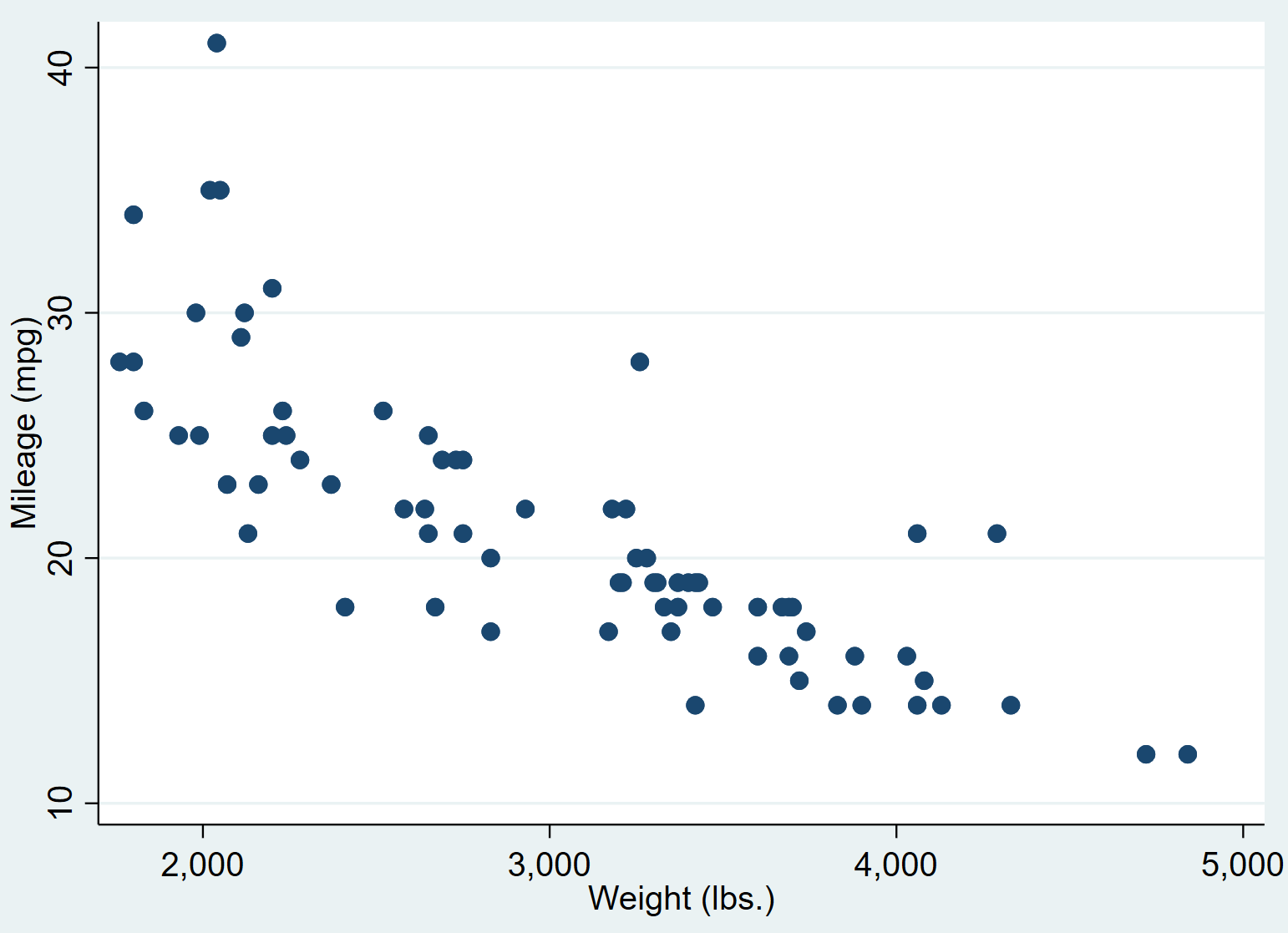
Wir können sehen, dass Autos mit höherem Gewicht tendenziell weniger Meilen pro Gallone haben. Um diesen Zusammenhang zu quantifizieren, führen wir nun eine einfache lineare Regression durch.

Schritt 4: Führen Sie eine einfache lineare Regression durch.

Geben Sie Folgendes in das Befehlsfeld ein, um eine einfache lineare Regression mit Gewicht als erklärender Variable und mpg als Antwortvariable durchzuführen.

Gewicht auf mpg zurückführen

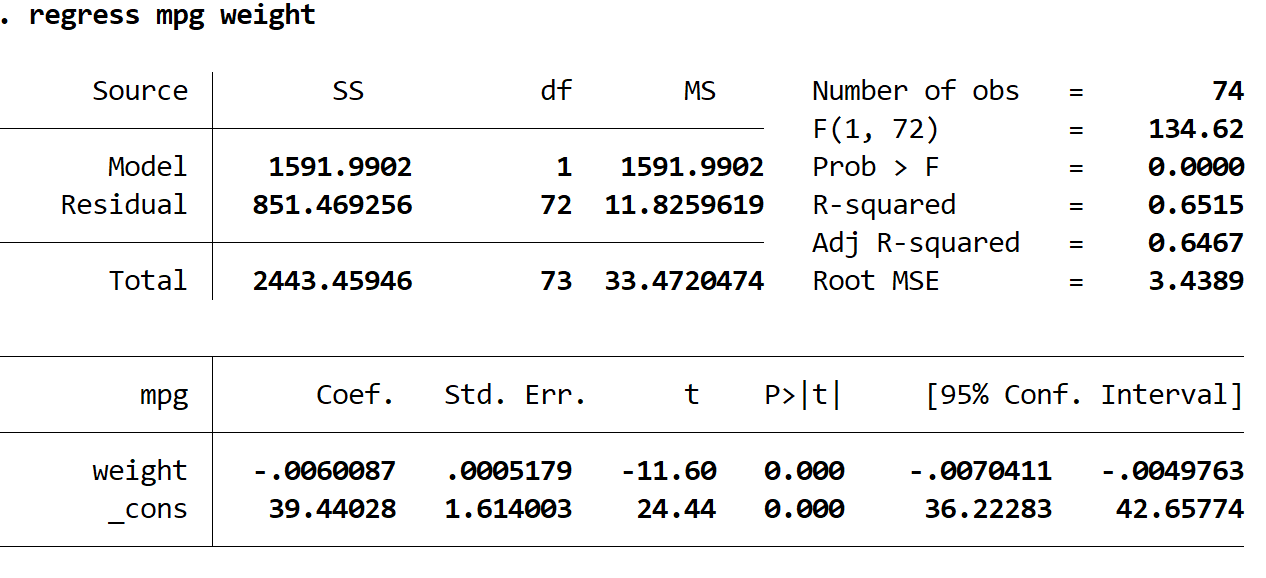
So interpretieren Sie die interessantesten Zahlen im Ergebnis:

R im Quadrat: 0,6515. Dies ist der Anteil der Varianz der Antwortvariablen, der durch die erklärende Variable erklärt werden kann. In diesem Beispiel können 65,15 % der Abweichung in mpg durch das Gewicht erklärt werden.

Koeffizient (Gewicht): -0,006. Dies gibt uns die durchschnittliche Änderung der Antwortvariablen an, die mit einem Anstieg der erklärenden Variablen um eine Einheit einhergeht. In diesem Beispiel ist jede Gewichtszunahme um ein Pfund mit einer durchschnittlichen Gewichtsabnahme von 0,006 mpg verbunden.

Koeffizient (_cons): 39,44028. Dies gibt uns den Durchschnittswert der Antwortvariablen an, wenn die erklärende Variable Null ist. In diesem Beispiel beträgt der durchschnittliche mpg 39,44028, wenn das Gewicht eines Autos Null ist. Dies ist nicht wirklich sinnvoll zu interpretieren, da das Gewicht eines Autos nicht Null sein kann, aber die Zahl 39,44028 ist notwendig, um eine Regressionsgleichung zu bilden.

P>|t| (Gewicht): 0,000. Dies ist der p-Wert, der der Teststatistik für das Gewicht zugeordnet ist. Da dieser Wert in diesem Fall unter 0,05 liegt, können wir daraus schließen, dass ein statistisch signifikanter Zusammenhang zwischen Gewicht und mpg besteht.

Regressionsgleichung: Schließlich können wir mithilfe der beiden Koeffizientenwerte eine Regressionsgleichung bilden. In diesem Fall wäre die Gleichung:

vorhergesagter mpg = 39,44028 – 0,0060087*(Gewicht)

Mit dieser Gleichung können wir den erwarteten Kraftstoffverbrauch für ein Auto angesichts seines Gewichts ermitteln. Ein Auto, das beispielsweise 4.000 Pfund wiegt, sollte einen Kraftstoffverbrauch von 15.405 mpg haben:

vorhergesagter mpg = 39,44028 – 0,0060087*(4000) = 15,405

Schritt 5: Melden Sie die Ergebnisse.

Abschließend möchten wir die Ergebnisse unserer einfachen linearen Regression berichten. Hier ist ein Beispiel dafür:

Eine lineare Regression wurde durchgeführt, um die Beziehung zwischen dem Gewicht eines Autos und seinen Meilen pro Gallone zu quantifizieren. Für die Analyse wurde eine Stichprobe von 74 Autos verwendet.

Die Ergebnisse zeigten, dass ein statistisch signifikanter Zusammenhang zwischen Gewicht und mpg (t = -11,60, p < 0,0001) bestand und dass das Gewicht 65,15 % der erklärten Variabilität bei mpg ausmachte.

Es stellte sich heraus, dass die Regressionsgleichung lautete:

vorhergesagter mpg = 39,44 – 0,006 (Gewicht)

Jedes zusätzliche Pfund war mit einer durchschnittlichen Verringerung um -0,006 Meilen pro Gallone verbunden.