Einfache zufallsstichprobe
In diesem Artikel erfahren Sie, was eine einfache Zufallsstichprobe ist und welche Arten einfacher Zufallsstichproben es gibt. Zusätzlich erklären wir anhand eines Beispiels, wie eine einfache Zufallsstichprobe durchgeführt wird. Abschließend erfahren Sie, welche Vor- und Nachteile eine einfache Zufallsstichprobe hat.
Was ist eine einfache Zufallsstichprobe?
In der Statistik ist die einfache Zufallsstichprobe eine probabilistische Methode zur Auswahl der Stichprobe für eine Studie. Das Hauptmerkmal der einfachen Zufallsstichprobe besteht darin, dass sie jedem Element der statistischen Grundgesamtheit die gleiche Wahrscheinlichkeit verleiht, in die untersuchte Stichprobe aufgenommen zu werden.
Bei der einfachen Zufallsstichprobe werden die Stichprobenelemente zufällig ausgewählt, sodass die resultierende Stichprobe völlig zufällig ist.
Daher ist bei Verwendung einer einfachen Zufallsstichprobe die Wahrscheinlichkeit, eine bestimmte Stichprobe zu erhalten, gleich der Wahrscheinlichkeit, eine beliebige andere Stichprobe zu erhalten. Wir werden weiter unten sehen, wie diese Wahrscheinlichkeit berechnet wird.
Bedenken Sie, dass es andere Möglichkeiten gibt, Personen aus einer Stichprobe auszuwählen. Die am häufigsten verwendeten Arten der Probenahme sind hauptsächlich:
- Einfache Zufallsstichprobe
- Geschichtete Stichprobe
- Systematische Probenahme
- Cluster-Sampling
Das Konzept der einfachen Zufallsstichprobe ist sicherlich die am einfachsten zu verstehende Art, erweist sich jedoch manchmal aufgrund seiner zufälligen Natur als die komplizierteste in der Umsetzung.
So führen Sie eine einfache Zufallsstichprobe durch
Die Schritte zur Durchführung einer einfachen Zufallsstichprobe sind wie folgt:
- Erstellen Sie eine Liste mit allen Elementen der Bevölkerung.
- Weisen Sie jedem Element in der Grundgesamtheit eine fortlaufende Nummer (1, 2, 3,…, n) zu.
- Stellen Sie die gewünschte Probengröße ein.
- Verwenden Sie einen Zufallszahlengenerator , um so viele Zahlen wie die gewählte Stichprobengröße zu generieren.
- Die den generierten Nummern zugeordneten Personen sind diejenigen, die als Teil der Stichprobe ausgewählt wurden.
Um Zufallszahlen zu generieren, gibt es mehrere Methoden, die traditionellsten sind die Lotteriemethode und die Zahlentabellenmethode:
- Bei der Lotteriemethode werden alle Zahlen in ein Kästchen gegeben, gemischt und dann nach dem Zufallsprinzip gezogen.
- Bei der Zahlentabellenmethode werden Zahlen zufällig aus einer Tabelle ausgewählt, die alle möglichen Zahlen enthält.
Sie können zwar auch eine der beiden vorherigen Methoden verwenden, diese erfordern jedoch mehr Zeit und eignen sich besser für kleinere Stichprobengrößen. Derzeit werden Computerprogramme verwendet, um Zufallszahlen schneller zu generieren, beispielsweise das Programm Excel.
Andererseits müssen Sie berücksichtigen, dass die Stichprobengröße ausreichend sein muss, um einen möglichst geringen Stichprobenfehler zu erzielen. Die ideale Stichprobengröße zu finden ist nicht trivial; Wenn Sie diesbezüglich Zweifel haben, können Sie auf unserer Website nach dem Artikel suchen, in dem wir erklären, wie das geht.
Beispiel für eine einfache Zufallsstichprobe
Sobald wir die Definition der einfachen Zufallsstichprobe kennengelernt haben, sehen wir ein gelöstes Beispiel dafür, wie diese Art der Stichprobe durchgeführt wird.
Wenn in einem Unternehmen beispielsweise 2000 Arbeitnehmer beschäftigt sind und wir eine statistische Studie mit einer Stichprobe von 400 Arbeitnehmern durchführen möchten, besteht der erste Schritt darin, mithilfe einer einfachen Zufallsstichprobe die Personen auszuwählen, die Teil der Stichprobe sein werden Jedem Mitarbeiter wird eine Nummer von 1 bis 2000 zugewiesen.
Nachdem die Nummern zugewiesen wurden, müssen wir 400 Nummern zufällig auswählen. In diesem Fall ist die Stichprobengröße recht groß, daher ist es am besten, Computersoftware wie Excel zu verwenden.
Anschließend werden diejenigen 400 Arbeitnehmer zur Teilnahme an der Studie ausgewählt, deren zugewiesene Anzahl im vorherigen Schritt ermittelt wurde.
In diesem Beispiel wurden 400 Elemente als ausreichend repräsentative Stichprobengröße angesehen, aber logischerweise ändert sich diese Zahl je nach Experiment.
Arten der einfachen Zufallsstichprobe
Es gibt zwei Arten der einfachen Zufallsstichprobe:
- Einfache Zufallsstichprobe mit Ersetzung : Das ausgewählte Element des Stichprobenrahmens wird zurückgegeben und kann erneut ausgewählt werden.
- Einfache Zufallsstichprobe ohne Ersatz : Der zur Stichprobe ausgewählte Artikel wird gelöscht und kann nicht mehr ausgewählt werden.
Die einfache Zufallsstichprobe mit Ersatz ist die einfachste Art der Stichprobe, da immer der exakt gleiche Vorgang wiederholt wird, um ein Element aus der Stichprobe auszuwählen. Allerdings wird die einfache ersatzlose Zufallsstichprobe häufiger eingesetzt, da sie präziser ist. Beide Arten werden im Folgenden näher erläutert.
Einfache Zufallsauswahl mit Ersatz
Bei der einfachen Zufallsstichprobe mit Ersetzung wird jedes ausgewählte Element wieder in den Stichprobenrahmen zurückgeführt, so dass die Möglichkeit einer erneuten Auswahl besteht.
Daher ist es möglich, eine Stichprobe zu erhalten, bei der ein einzelner Artikel mehrfach ausgewählt wird, obwohl dies natürlich sehr unwahrscheinlich ist.
Mathematisch gesehen ist dies eine sehr einfache Art der Stichprobenziehung, da die Wahrscheinlichkeiten jeder Extraktion gleich sind. Aus diesem Grund beginnt man normalerweise vor anderen mit dem Studium dieser Stichprobentechnik.
Bei der einfachen Zufallsstichprobe mit Ersetzung lässt sich die Wahrscheinlichkeit, eine Stichprobe mit einer bestimmten Reihenfolge zu erhalten, nach folgender Formel berechnen:
![]()
Sei
![]()
die Gesamtzahl der Elemente der Bevölkerung und
![]()
die Anzahl der unabhängigen Extraktionen, die durchgeführt werden.
Wenn die Reihenfolge hingegen keine Rolle spielt, wird die Wahrscheinlichkeit, eine Probe zu erhalten, mithilfe des folgenden Ausdrucks berechnet:
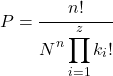
Gold
![]()
ist die Anzahl der unabhängigen Extraktionen,
![]()
die Anzahl der verschiedenen Elemente in der Probe und
![]()
wie oft das Element angezeigt werden soll
![]()
in der Probe.
Schließlich gilt es, die Wahrscheinlichkeit der Einbeziehung des Elements zu ermitteln
![]()
, also die Wahrscheinlichkeit, das Element einzubeziehen
![]()
Im Beispiel soll folgende Formel verwendet werden:
![]()
Einfache Zufallsauswahl ohne Ersatz
Bei der einfachen ersatzlosen Zufallsauswahl werden aus einer Stichprobe so viele Personen ausgewählt, wie die gewünschte Stichprobengröße angibt, sodass nicht jede einzelne Person erneut ausgewählt werden kann, wenn sie einmal ausgewählt wurde. Daher wird jedes ausgewählte Element gelöscht und nicht ersetzt.
Wenn wir von einfacher Zufallsstichprobe sprechen, beziehen wir uns normalerweise auf die Stichprobe, bei der einzelne Personen nicht ersetzt werden, da sie in der Praxis am häufigsten verwendet wird.
Um die Wahrscheinlichkeit zu bestimmen, bei einer einfachen Zufallsstichprobe mit Ersetzung eine Stichprobe mit einer bestimmten Reihenfolge zu erhalten, wird die folgende Formel verwendet:
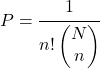
Sei
![]()
die Gesamtzahl der Elemente in der Population und
![]()
die Anzahl der durchzuführenden abhängigen Extraktionen.
Wenn andererseits die Extraktionsreihenfolge nicht berücksichtigt werden muss, ist die Wahrscheinlichkeit, eine Probe zu erhalten, gleich:
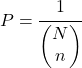
Schließlich wird die Wahrscheinlichkeit der Einbeziehung eines Elements in eine einfache Zufallsstichprobe ohne Ersatz durch Anwendung der Laplace-Regel berechnet:
![]()
Vor- und Nachteile der einfachen Zufallsstichprobe
Die einfache Zufallsstichprobe hat folgende Vor- und Nachteile:
| Vorteil | Nachteile |
|---|---|
| Einfach zu verstehen. | Eine Liste aller Elemente der Bevölkerung ist erforderlich. |
| Alle möglichen Proben sind gleichwahrscheinlich. | Dies kann bei großen Stichprobengrößen sehr teuer sein. |
| In der Regel werden repräsentative Proben entnommen. | Es treten tendenziell größere Stichprobenfehler auf. |
| Für die Probenahme sind keine technischen Kenntnisse erforderlich. | Das Wissen, das der Forscher möglicherweise auf dem untersuchten Gebiet hat, wird nicht ausgenutzt. |
| Ermöglicht die schnelle Berechnung von Durchschnittswerten und Abweichungen. | Wenn die Stichprobe zu klein ist, ist sie möglicherweise nicht repräsentativ. |
| Zur Analyse der Daten gibt es Statistiksoftware. | Nicht geeignet für Studien, die Einzelinterviews erfordern. |
Wie wir gesehen haben, besteht eines der Hauptmerkmale der einfachen Zufallsstichprobe darin, dass sie leicht zu verstehen und zu erklären ist. Tatsächlich muss die Person, die die Probenahme durchführt, kein Experte auf dem Gebiet der Analyse sein. Dies ist jedoch sowohl eine Stärke als auch eine Schwäche, da bei anderen Stichprobenarten das Wissen des Analysten genutzt werden kann, um eine bessere Stichprobe zu erzielen.
Da die Stichprobe zufällig ist, sind die Wahrscheinlichkeiten, dass dieses oder jenes Element zur Bildung der untersuchten Stichprobe herangezogen wird, im Gegensatz zu anderen Stichprobenarten gleich wahrscheinlich.
Obwohl in der Regel repräsentative Stichproben der Bevölkerung gewonnen werden, ist der Stichprobenfehler bei der einfachen Zufallsstichprobe im Vergleich zu anderen Stichprobenarten groß. Darüber hinaus ist die Stichprobe möglicherweise nicht einmal repräsentativ, wenn die Größe der Personen klein ist.
Eine sehr attraktive Eigenschaft der einfachen Zufallsstichprobe besteht darin, dass sie mithilfe von Computerprogrammen durchgeführt werden kann, wodurch statistische Berechnungen schnell durchgeführt werden können.
Abschließend ist zu beachten, dass eine einfache Zufallsstichprobe insbesondere bei weit verstreuten Populationen teurer sein kann als andere Stichprobenarten, da möglicherweise mehr Ressourcen für die Forschung eingesetzt werden müssen. Da es sich beispielsweise um eine Zufallsstichprobe handelt, können die für die Durchführung der Studie ausgewählten Personen geografisch weit verstreut sein und die Durchführung persönlicher Interviews wäre daher viel teurer.