Was ist somers' d? (definition & #038; beispiel)

Somers‘ D , kurz für Somers‘ Delta, ist ein Maß für die Stärke und Richtung der Assoziation zwischen einer ordinalen abhängigen Variablen und einer ordinalen unabhängigen Variablen.

Eine ordinale Variable ist eine Variable, bei der die Werte eine natürliche Reihenfolge haben (z. B. „schlecht“, „neutral“, „gut“).

Der Wert von Somers‘ D liegt zwischen -1 und 1, wobei:

• -1: Zeigt an, dass nicht alle Variablenpaare übereinstimmen
• 1: zeigt an, dass alle Variablenpaare übereinstimmen

Somers‘ D wird in der Praxis für viele nichtparametrische statistische Methoden verwendet.

Somers‘ D: Definition

Bei zwei Variablen X und Y können wir sagen:

• Zwei Paare (x _i , y _i ) und (x _j , y _j ) sind konkordant, wenn die Ränge der beiden Elemente übereinstimmen.
• Zwei Paare (x _i , y _i ) und (x _j , y _j ) sind nicht übereinstimmend wenn die Ränge der beiden Elemente übereinstimmen.

Anschließend können wir Somers‘ D mithilfe der folgenden Formel berechnen:

Somers‘ D = ( _NC – N _D ) / ( _NC + N _D + N _T )

Gold:

• N _C : Die Anzahl der übereinstimmenden Paare
• _ND : Die Anzahl der nicht übereinstimmenden Paare
• N _T : Die Anzahl der gebundenen Paare

Der resultierende Wert liegt immer zwischen -1 und 1.

Somers‘ D: Beispiel in R

Angenommen, ein Lebensmittelgeschäft möchte die Beziehung zwischen den folgenden zwei Ordinalvariablen auswerten:

• Gesamtfreundlichkeit der Kassiererin (Rang 1 bis 3)
• Gesamtzufriedenheit mit dem Kundenerlebnis (ebenfalls Rang 1 bis 3)

Sie sammeln die folgenden Bewertungen aus einer Stichprobe von 10 Kunden:

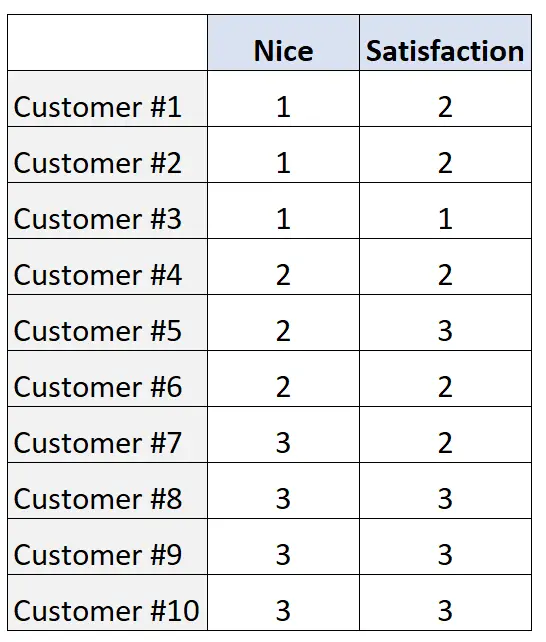
Um die Beziehung zwischen den beiden Variablen zu quantifizieren, können wir Somers‘ D mithilfe des folgenden Codes in R berechnen:

 #enter data
nice <- c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3)
satisfaction <- c(2, 2, 1, 2, 3, 2, 2, 3, 3, 3)

#load DescTools package
library(DescTools)

#calculate Somers' D
SomersDelta(nice, satisfaction)

[1] 0.6896552

Es stellt sich heraus, dass Somers‘ D 0,6896552 beträgt.

Da dieser Wert ziemlich nahe bei 1 liegt, deutet dies darauf hin, dass zwischen den beiden Variablen eine ziemlich starke positive Beziehung besteht.

Das macht intuitiv Sinn: Kunden, die Kassierer als netter bewerten, neigen auch dazu, ihre Gesamtzufriedenheit höher einzuschätzen.

Zusätzliche Ressourcen

Eine Einführung in den Pearson-Korrelationskoeffizienten
Eine Einführung in Kendalls Tau