So erstellen und interpretieren sie qq-plots in spss

Ein QQ-Plot , kurz für „Quantil-Quantil“, wird häufig verwendet, um zu beurteilen, ob eine Variable normalverteilt ist oder nicht.

In diesem Tutorial wird erläutert, wie Sie ein QQ-Diagramm in SPSS erstellen und interpretieren.

Beispiel: QQ-Plot in SPSS

Nehmen wir an, wir haben den folgenden Datensatz in SPSS, der die Punkte pro Spiel für 25 verschiedene Basketballspieler anzeigt:

Mit den folgenden Schritten können wir in SPSS ein QQ-Diagramm erstellen, um zu bestimmen, ob die variablen Punkte normalverteilt sind oder nicht.

Schritt 1: Wählen Sie die Option „Erkunden“.

Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Beschreibende Statistik“ und dann auf „Erkunden“ :

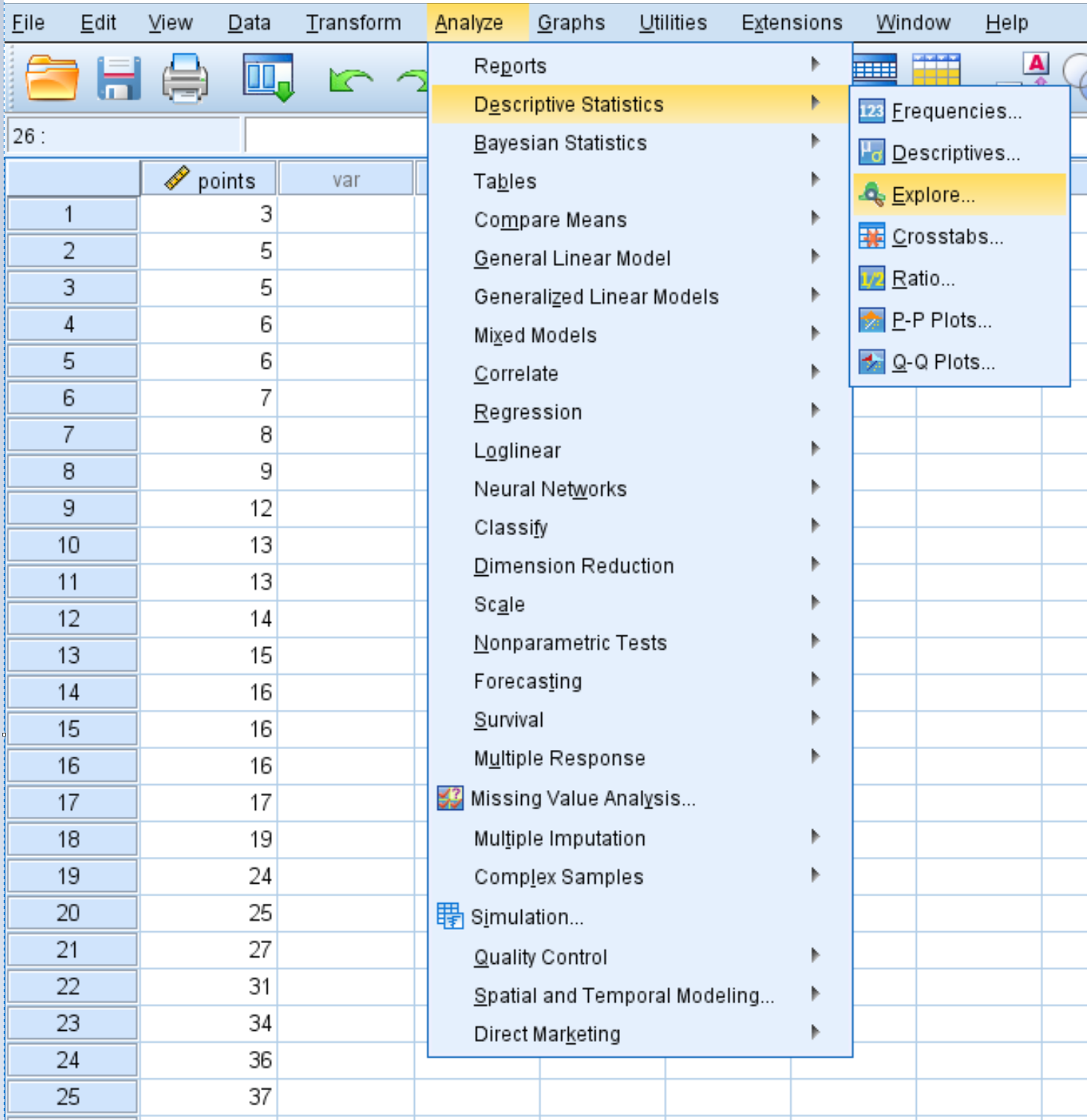
Schritt 2: Erstellen Sie das QQ-Diagramm.

Ziehen Sie die variablen Punkte in den Bereich mit der Bezeichnung „Abhängige Liste“. Klicken Sie dann auf die Schaltfläche „Plots“ und stellen Sie sicher, dass das Kontrollkästchen neben „Normality Plots with Tests“ aktiviert ist. Klicken Sie dann auf Weiter . Klicken Sie dann auf OK .

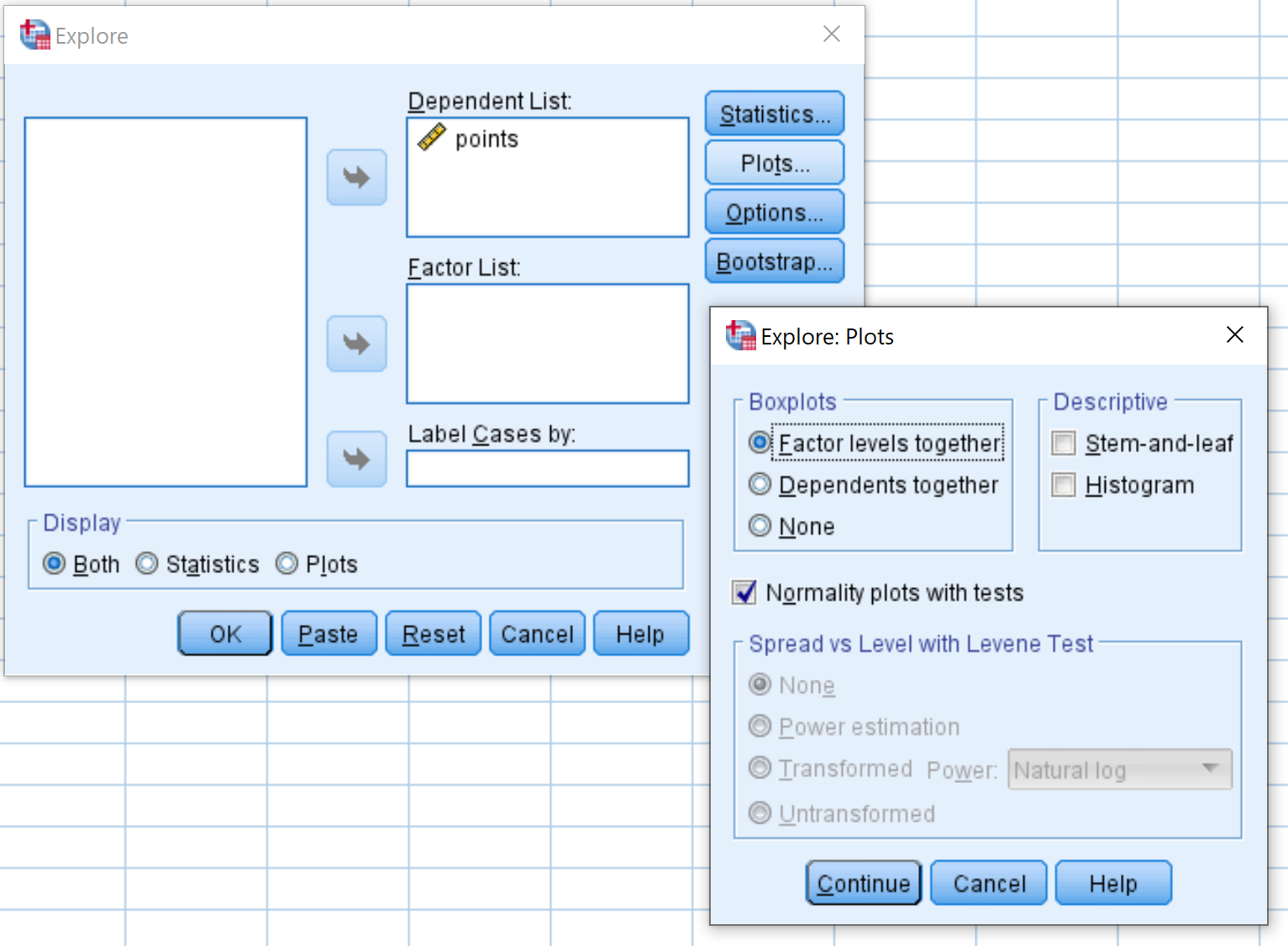
Schritt 3: Interpretieren Sie das QQ-Diagramm.

Sobald Sie auf OK klicken, wird das folgende QQ-Diagramm angezeigt:

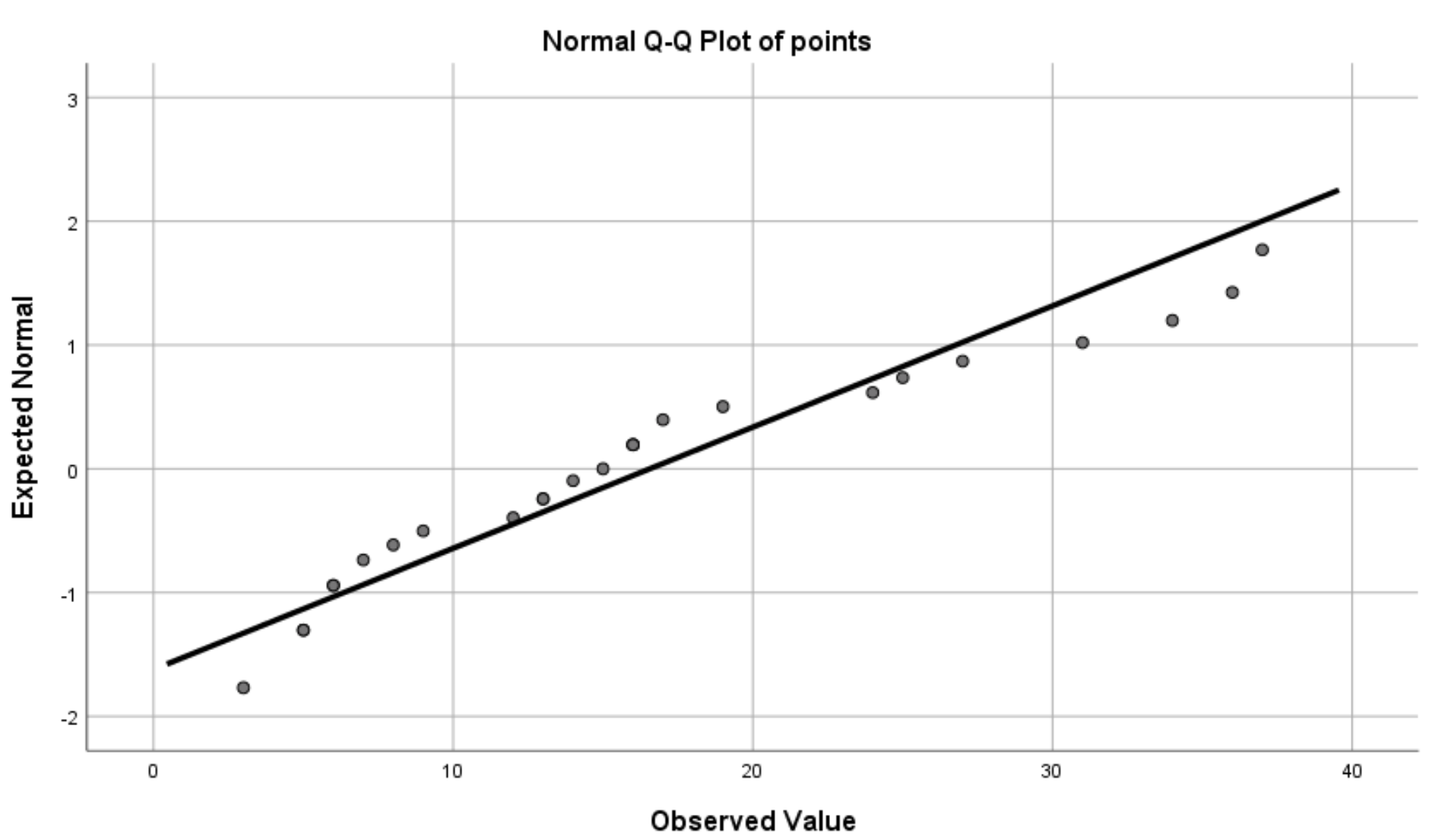
Die Idee hinter einem QQ-Diagramm ist einfach: Wenn die Residuen einer ungefähr geraden Linie in einem Winkel von 45 Grad folgen, sind die Residuen ungefähr normalverteilt.

Wir können in unserem QQ-Diagramm oben sehen, dass die Residuen dazu neigen, etwas von der 45-Grad-Linie abzuweichen, insbesondere an den Enden, was darauf hindeuten könnte, dass sie nicht normalverteilt sind.

Obwohl es sich bei einem QQ-Diagramm nicht um einen formalen statistischen Test handelt, bietet er eine einfache Möglichkeit, visuell zu überprüfen, ob die Residuen normalverteilt sind oder nicht.

Für zwei formale statistische Tests siehe die p-Werte des Kolmogorov-Smirnov-Tests und des Shapiro-Wilk-Tests, die über dem QQ-Diagramm angezeigt werden:

• Kolmogorov-Smirnov-Normalitätstest P-Wert: 0,086
• P-Wert des Shapiro-Wilk-Normalitätstests: 0,042

Da diese beiden Werte nahe bei 0,05 liegen, deutet dies darauf hin, dass die variablen Punkte möglicherweise nicht normalverteilt sind.