Einfaktorielle anova: definition, formel und beispiel
Eine einfaktorielle ANOVA („Varianzanalyse“) vergleicht die Mittelwerte von drei oder mehr unabhängigen Gruppen, um festzustellen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten der entsprechenden Population besteht.
In diesem Tutorial wird Folgendes erklärt:
- Die Motivation, eine einfaktorielle ANOVA durchzuführen.
- Die Annahmen, die erfüllt sein müssen, um eine einfaktorielle ANOVA durchzuführen.
- Der Prozess zur Durchführung einer einfaktoriellen ANOVA.
- Ein Beispiel für die Durchführung einer einfaktoriellen ANOVA.
Einfaktorielle ANOVA: Motivation
Angenommen, wir möchten wissen, ob drei verschiedene Prüfungsvorbereitungsprogramme zu unterschiedlichen Durchschnittsergebnissen bei einer Hochschulaufnahmeprüfung führen. Da es im ganzen Land Millionen von Oberstufenschülern gibt, wäre es zu zeitaufwändig und teuer, jeden Schüler aufzusuchen und ihn eines der Prüfungsvorbereitungsprogramme nutzen zu lassen.
Stattdessen könnten wir drei Zufallsstichproben von 100 Studenten aus der Grundgesamtheit auswählen und jeder Stichprobe erlauben, eines von drei Prüfungsvorbereitungsprogrammen zu nutzen, um sich auf die Prüfung vorzubereiten. Dann könnten wir die Ergebnisse jedes Schülers aufzeichnen, sobald er die Prüfung abgelegt hat.
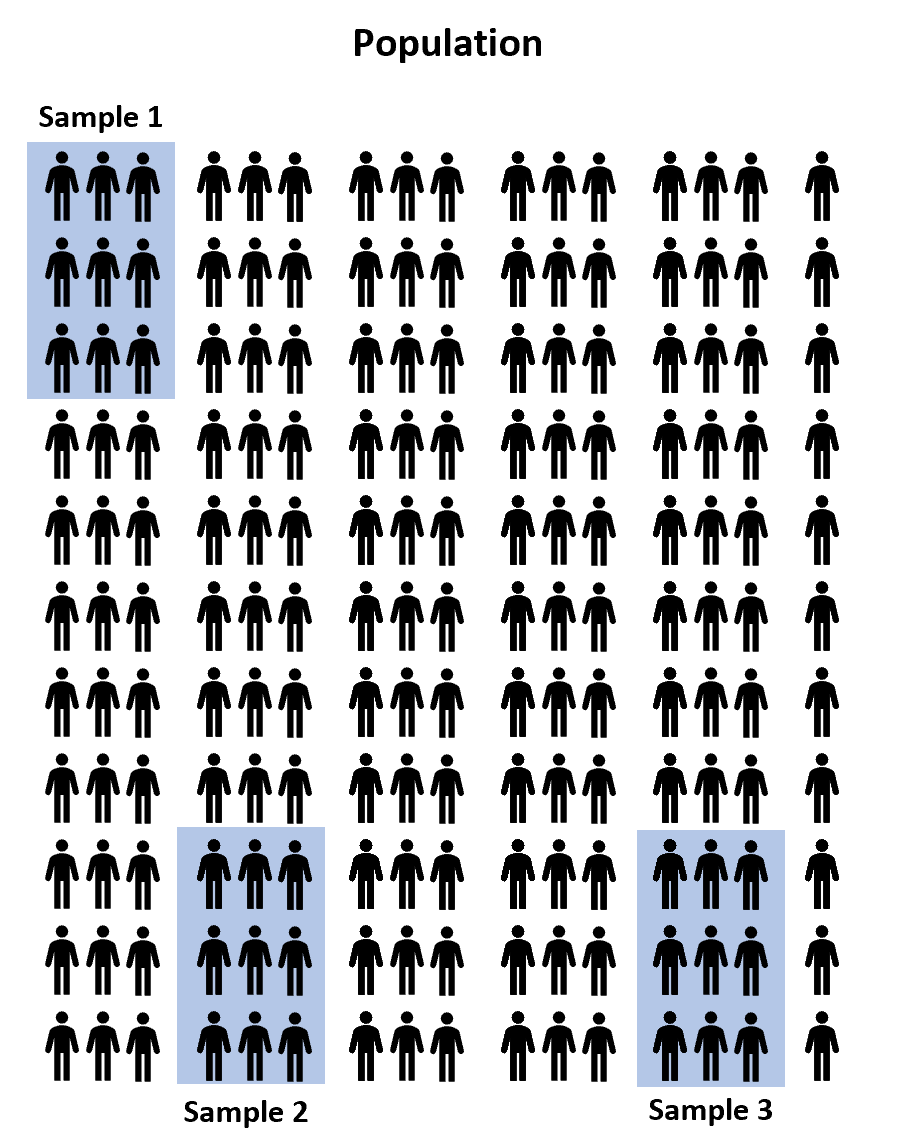
Es ist jedoch praktisch garantiert, dass die durchschnittliche Prüfungspunktzahl zwischen den drei Stichproben zumindest geringfügig unterschiedlich sein wird. Die Frage ist, ob dieser Unterschied statistisch signifikant ist . Glücklicherweise ermöglicht uns eine einfaktorielle ANOVA, diese Frage zu beantworten.
Einfaktorielle ANOVA: Annahmen
Damit die Ergebnisse einer einfaktoriellen ANOVA gültig sind, müssen die folgenden Annahmen erfüllt sein:
1. Normalität – Jede Stichprobe wurde aus einer normalverteilten Grundgesamtheit gezogen.
2. Gleiche Varianzen – Die Varianzen der Grundgesamtheiten, aus denen die Stichproben gezogen werden, sind gleich. Sie können den Bartlett-Test verwenden, um diese Hypothese zu testen.
3. Unabhängigkeit – Die Beobachtungen innerhalb jeder Gruppe sind unabhängig voneinander und die Beobachtungen innerhalb der Gruppen wurden durch Zufallsstichproben ermittelt.
Weitere Informationen zur Überprüfung dieser Annahmen finden Sie in diesem Artikel .
Einfaktorielle ANOVA: der Prozess
Eine einfaktorielle ANOVA verwendet die folgenden Null- und Alternativhypothesen:
- H 0 (Nullhypothese): μ 1 = μ 2 = μ 3 = … = μ k (alle Populationsmittelwerte sind gleich)
- H 1 (Alternativhypothese): Mindestens ein Populationsmittelwert ist unterschiedlich ausruhen
Normalerweise verwenden Sie eine Statistiksoftware (wie R, Excel, Stata, SPSS usw.), um eine einfaktorielle ANOVA durchzuführen, da die manuelle Durchführung mühsam ist.
Unabhängig von der verwendeten Software erhalten Sie als Ausgabe folgende Tabelle:
| Quelle | Summe der Quadrate (SS) | df | Mittlere Quadrate (MS) | F | P |
|---|---|---|---|---|---|
| Behandlung | RSS | df r | MSR | MSR/MSE | F df r , df e |
| Fehler | ESS | df e | MSE | ||
| Gesamt | OHS | df t |
Gold:
- SSR: Summe der Quadrate-Regression
- SSE: Summe der quadratischen Fehler
- SST: Gesamtsumme der Quadrate (SST = SSR + SSE)
- df r : Regressionsfreiheitsgrade (df r = k-1)
- df e : Fehlerfreiheitsgrade (df e = nk)
- df t : Gesamtfreiheitsgrade (df t = n-1)
- k: Gesamtzahl der Gruppen
- n: Gesamtbeobachtungen
- MSR: mittlere quadratische Regression (MSR = SSR/ dfr )
- MSE: mittlerer quadratischer Fehler (MSE = SSE/df e )
- F: Die F-Teststatistik (F = MSR/MSE)
- p: Der Wert p, der F dfr, dfe entspricht
Wenn der p-Wert unter dem gewählten Signifikanzniveau (z. B. 0,05) liegt, können Sie die Nullhypothese ablehnen und daraus schließen, dass sich mindestens einer der Mittelwerte der Grundgesamtheit von den anderen unterscheidet.
Hinweis: Wenn Sie die Nullhypothese ablehnen, bedeutet dies, dass sich mindestens einer der Grundgesamtheitsmittelwerte von den anderen unterscheidet, die ANOVA-Tabelle gibt jedoch nicht an, welche Grundgesamtheitsmittelwerte unterschiedlich sind. Um dies festzustellen, müssen Sie Post-hoc-Tests durchführen, die auch als „Mehrfachvergleichstests“ bezeichnet werden.
Einfaktorielle ANOVA: Beispiel
Angenommen, wir möchten wissen, ob drei verschiedene Prüfungsvorbereitungsprogramme zu unterschiedlichen Durchschnittsergebnissen bei einer bestimmten Prüfung führen. Um dies zu testen, rekrutieren wir 30 Studierende für die Teilnahme an einer Studie und teilen sie in drei Gruppen auf.
Den Schülern jeder Gruppe wird nach dem Zufallsprinzip zugeteilt , dass sie in den folgenden drei Wochen eines von drei Prüfungsvorbereitungsprogrammen nutzen sollen, um sich auf eine Prüfung vorzubereiten. Am Ende der drei Wochen legen alle Studierenden die gleiche Prüfung ab.
Die Prüfungsergebnisse für jede Gruppe sind unten aufgeführt:

Um eine einfache ANOVA für diese Daten durchzuführen, verwenden wir den Statistics One-Way ANOVA-Rechner mit der folgenden Eingabe:

Aus der Ausgabetabelle sehen wir, dass die F-Teststatistik 2,358 und der entsprechende p-Wert 0,11385 beträgt.

Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.
Das bedeutet, dass uns keine ausreichenden Beweise dafür vorliegen, dass es einen statistisch signifikanten Unterschied zwischen den durchschnittlichen Prüfungsergebnissen der drei Gruppen gibt.
Zusätzliche Ressourcen
In den folgenden Artikeln wird erläutert, wie eine einfaktorielle ANOVA mit unterschiedlicher Statistiksoftware durchgeführt wird:
So führen Sie eine einfaktorielle ANOVA in Excel durch
So führen Sie eine einfaktorielle ANOVA in R durch
So führen Sie eine einfaktorielle ANOVA in Python durch
So führen Sie eine einfaktorielle ANOVA in SAS durch
So führen Sie eine einfaktorielle ANOVA in SPSS durch
So führen Sie eine einfaktorielle ANOVA in Stata durch
So führen Sie eine einfaktorielle ANOVA auf einem TI-84-Rechner durch
Online-Rechner für einfaktorielle ANOVA