So führen sie eine einfaktorielle anova in excel durch

Mithilfe einer einfaktoriellen ANOVA („Varianzanalyse“) wird ermittelt, ob zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen ein statistisch signifikanter Unterschied besteht.

In diesem Tutorial wird erläutert, wie Sie eine einfaktorielle ANOVA in Excel durchführen.

Beispiel: Einfaktorielle ANOVA in Excel

Angenommen, ein Forscher rekrutiert 30 Studenten für die Teilnahme an einer Studie. Den Studierenden wird nach dem Zufallsprinzip zugewiesen, dass sie in den nächsten drei Wochen eine von drei Lerntechniken anwenden, um sich auf eine Prüfung vorzubereiten. Am Ende der drei Wochen absolvieren alle Schüler den gleichen Test.

Die Testergebnisse der Schüler sind unten aufgeführt:

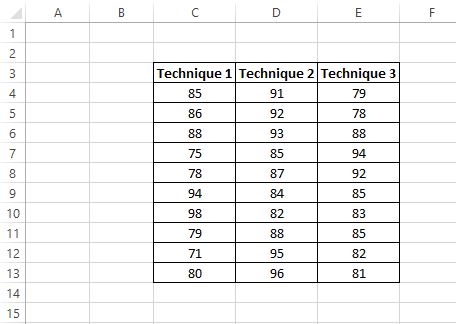
Der Forscher möchte eine einfache ANOVA durchführen, um festzustellen, ob die Durchschnittswerte in den drei Gruppen gleich sind.

Um eine einfaktorielle ANOVA in Excel durchzuführen, gehen Sie zur Registerkarte „Daten“ und klicken Sie dann in der Gruppe „Analyse“ auf die Option „Datenanalyse“ .

Wenn die Option „Datenanalyse“ nicht angezeigt wird , müssen Sie zunächst die kostenlose Analysis ToolPak- Software laden.

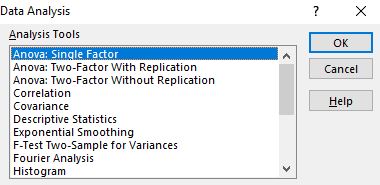
Sobald Sie darauf klicken, erscheint ein Fenster mit verschiedenen Scan-Tool-Optionen. Wählen Sie Anova: Einzelfaktor aus und klicken Sie dann auf OK .

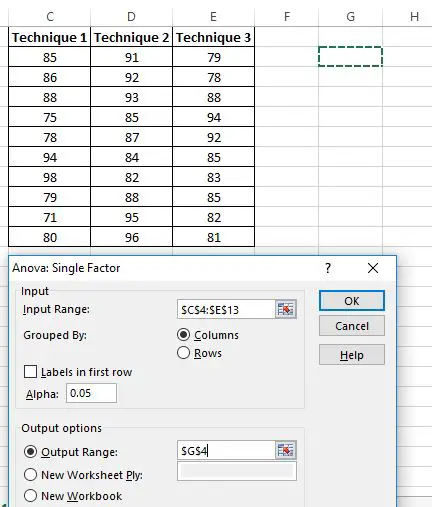
Es erscheint ein neues Fenster, in dem Sie nach einem Eingabebereich gefragt werden. Sie können entweder einen Rahmen um Ihre Daten ziehen oder den Datenbereich manuell eingeben. In diesem Fall befinden sich unsere Daten in den Zellen C4:E13 .

Wählen Sie als Nächstes eine Alpha- Stufe für den Test aus. Standardmäßig beträgt diese Zahl 0,05. In diesem Fall belasse ich es bei 0,05.

Wählen Sie abschließend eine Zelle für den Ausgabebereich aus, in der die Ergebnisse der einfaktoriellen ANOVA angezeigt werden. In diesem Fall wähle ich Zelle G4 .

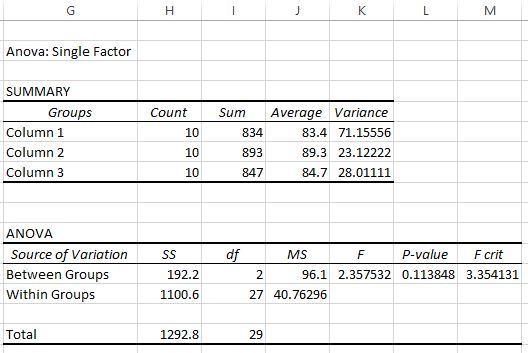
Sobald Sie auf OK klicken, wird das Ergebnis der einfaktoriellen ANOVA angezeigt:

Interpretation des Ergebnisses

In der Ausgabe werden zwei Tabellen angezeigt. Die erste ist eine Übersichtstabelle, die die Anzahl der Testergebnisse in jeder Gruppe, die Summe der Testergebnisse, den Mittelwert der Testergebnisse und die Varianz der Testergebnisse anzeigt.

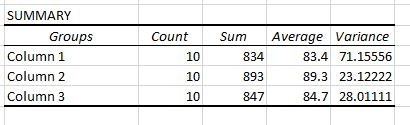
Denken Sie daran, dass eine einfaktorielle ANOVA verwendet wird, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr Gruppen besteht.

Aus dieser ersten Tabelle können wir ersehen, dass die durchschnittliche Punktzahl für jede der drei Gruppen unterschiedlich ist. Um jedoch zu wissen, ob diese Unterschiede statistisch signifikant sind, müssen wir uns die zweite Tabelle ansehen.

Die zweite Tabelle zeigt die F-Teststatistik, den kritischen F-Wert und den p-Wert:

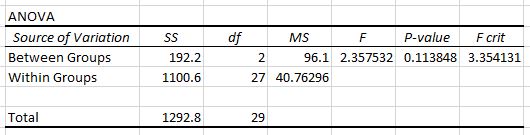
In diesem Fall beträgt die F-Teststatistik 2,3575 und der kritische Wert von F beträgt 3,3541 . Da die F-Teststatistik unter dem kritischen Wert von F liegt, verfügen wir nicht über ausreichende Beweise, um die Nullhypothese abzulehnen, dass die Mittelwerte der drei Gruppen gleich sind.

Das bedeutet, dass uns keine ausreichenden Beweise dafür vorliegen, dass es einen Unterschied in den Testergebnissen zwischen den drei Studientechniken gibt.

Wir könnten auch den p-Wert verwenden, um zu derselben Schlussfolgerung zu gelangen. In diesem Fall beträgt der p-Wert 0,1138 und liegt damit über dem Alpha-Wert von 0,05 .

Das bedeutet, dass wir nicht über ausreichende Beweise verfügen, um die Nullhypothese, dass die Mittelwerte der drei Gruppen gleich sind, zurückzuweisen.

Hinweis: In Fällen, in denen Sie die Nullhypothese ablehnen, können Sie einen Tukey-Kramer-Post-hoc-Test durchführen, um genau zu bestimmen, welche Gruppenmittelwerte unterschiedlich sind.