So führen sie eine einfaktorielle anova in spss durch

Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht.

Diese Art von Test wird als einfaktorielle ANOVA bezeichnet, da wir den Einfluss einer Prädiktorvariablen auf eine Antwortvariable analysieren.

Wären wir stattdessen an der Auswirkung zweier Prädiktorvariablen auf eine Antwortvariable interessiert, könnten wir eine zweifaktorielle ANOVA durchführen.

In diesem Tutorial wird erläutert, wie Sie eine einfaktorielle ANOVA in SPSS durchführen.

Beispiel: Einfaktorielle ANOVA in SPSS

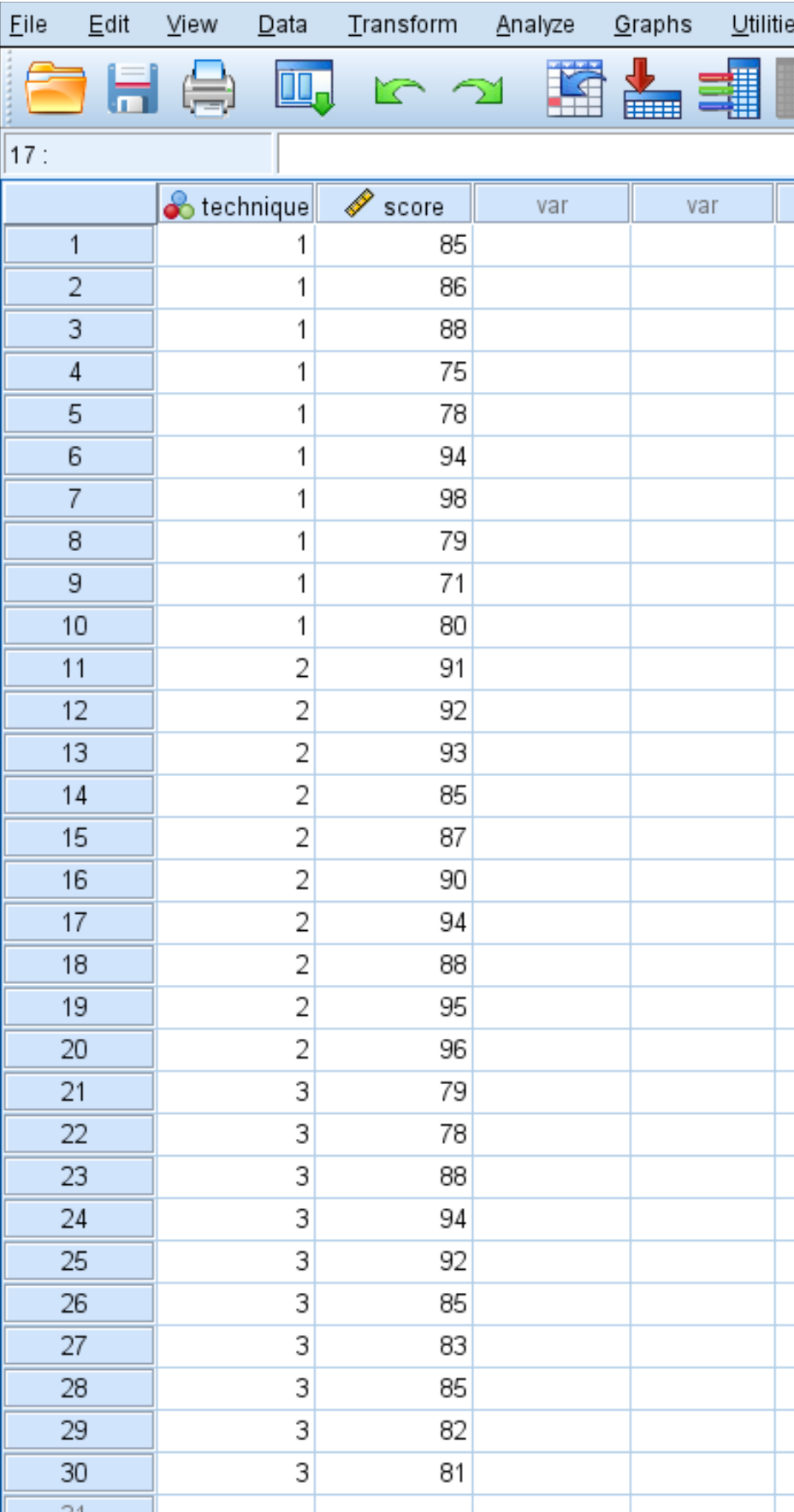
Angenommen, ein Forscher rekrutiert 30 Studenten für die Teilnahme an einer Studie. Den Studierenden wird nach dem Zufallsprinzip zugewiesen, dass sie im darauffolgenden Monat eine von drei Lerntechniken anwenden, um sich auf eine Prüfung vorzubereiten. Am Ende des Monats absolvieren alle Schüler den gleichen Test.

Die Testergebnisse der Schüler sind unten aufgeführt:

Führen Sie die folgenden Schritte aus, um eine einfache ANOVA durchzuführen und zu bestimmen, ob die Durchschnittswerte in den drei Gruppen gleich sind.

Schritt 1: Visualisieren Sie die Daten.

Zunächst erstellen wir Boxplots, um die Verteilung der Testergebnisse für jede der drei Lerntechniken zu visualisieren. Klicken Sie auf die Registerkarte „Diagramme“ und dann auf „Chart Builder“ .

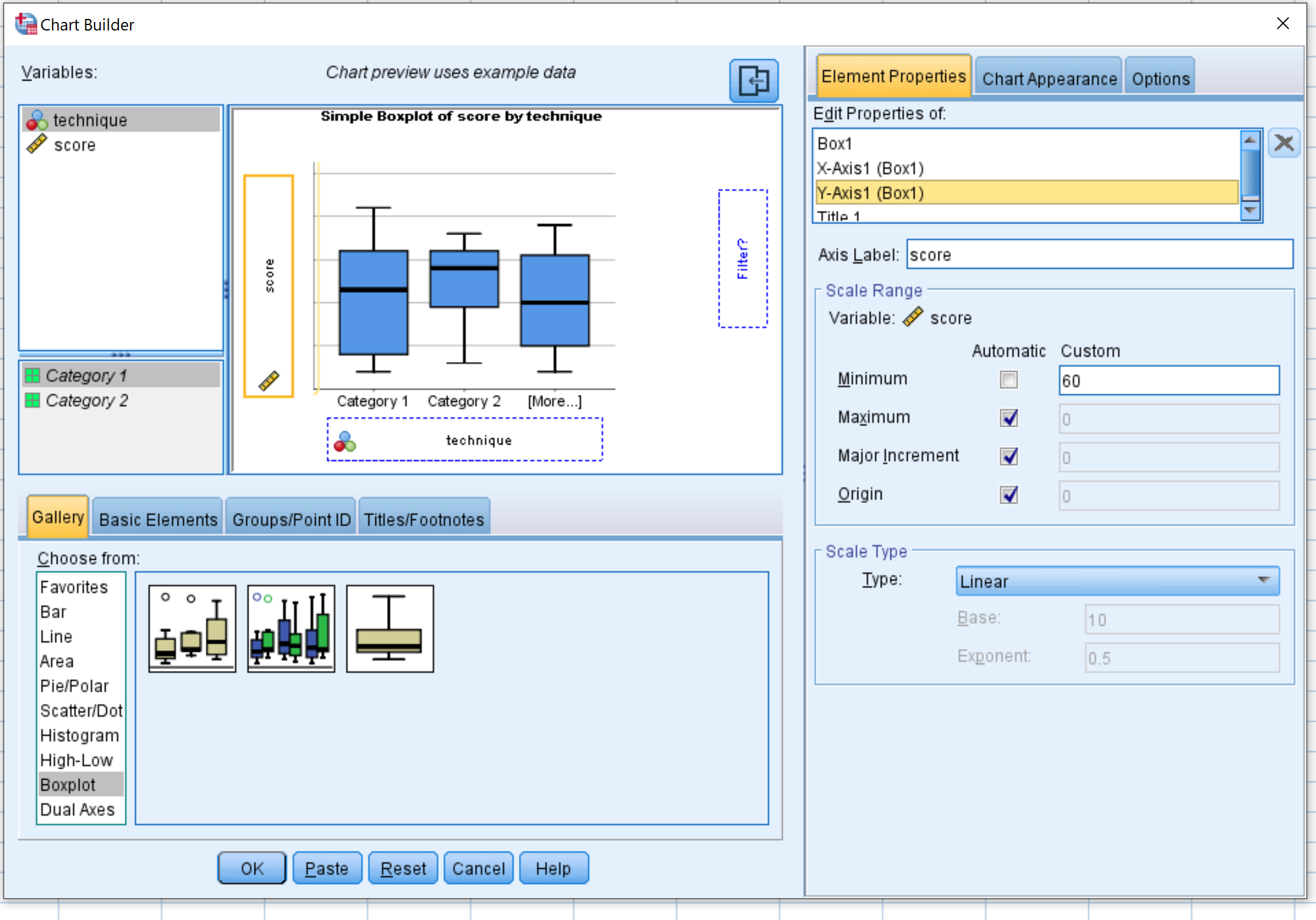
Wählen Sie Boxplot im Fenster „Wählen aus:“ aus. Ziehen Sie dann das erste Diagramm mit der Bezeichnung „Einfacher Boxplot“ in das Hauptbearbeitungsfenster. Ziehen Sie die technische Variable auf die x-Achse und den Score auf die y-Achse.

Klicken Sie dann auf Elementeigenschaften und dann auf Y1-Achse . Ändern Sie den Mindestwert auf 60. Klicken Sie dann auf OK .

Die folgenden Boxplots werden angezeigt:

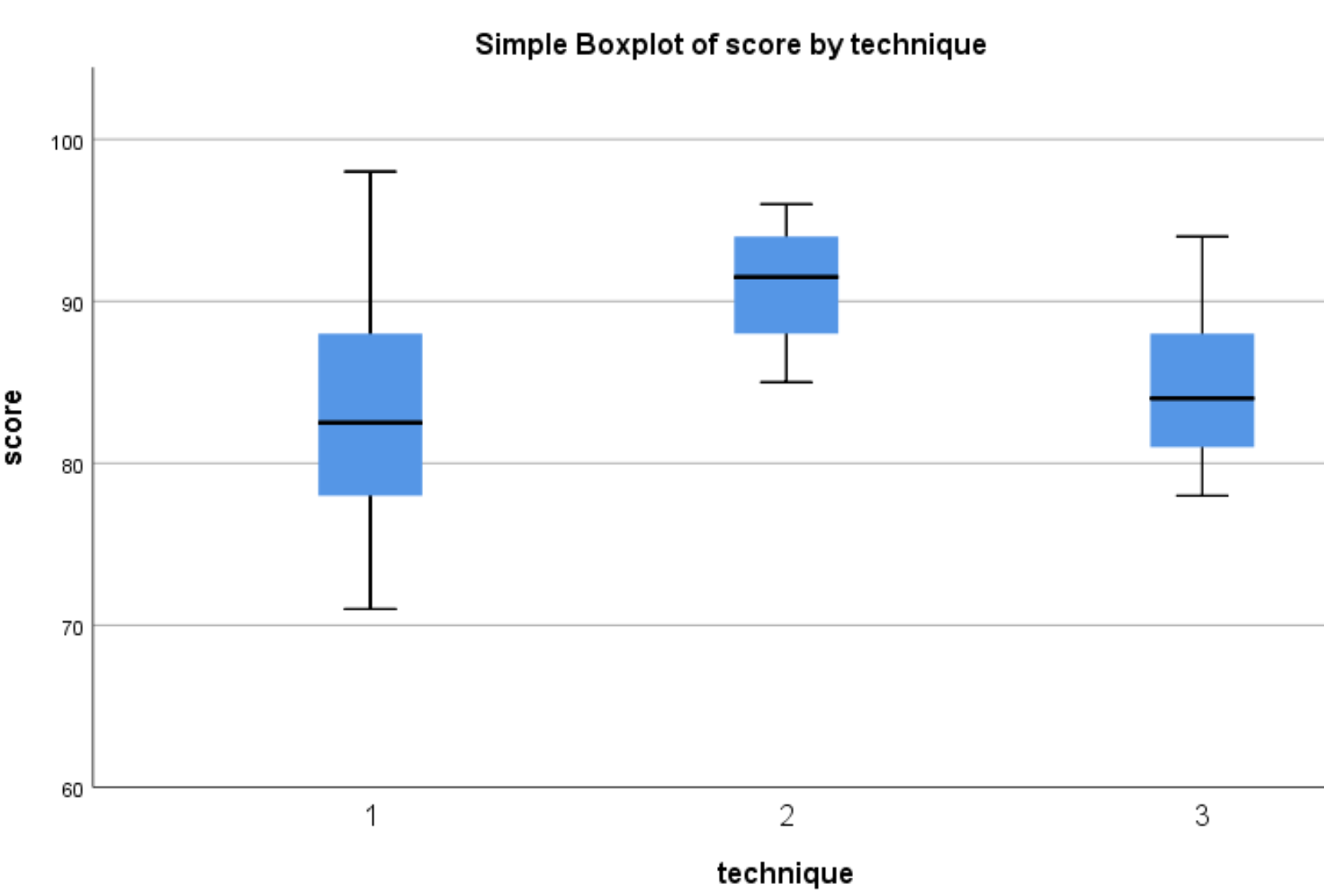
Wir können sehen, dass die Verteilung der Testergebnisse bei Schülern, die Technik 2 verwendet haben, tendenziell höher ist als bei Schülern, die Techniken 1 und 3 verwendet haben. Um festzustellen, ob diese Ergebnisunterschiede statistisch signifikant sind, führen wir eine einfaktorielle ANOVA durch.

Schritt 2: Führen Sie eine einfaktorielle ANOVA durch.

Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Mittelwerte vergleichen “ und dann auf „Einfaktorielle ANOVA“ .

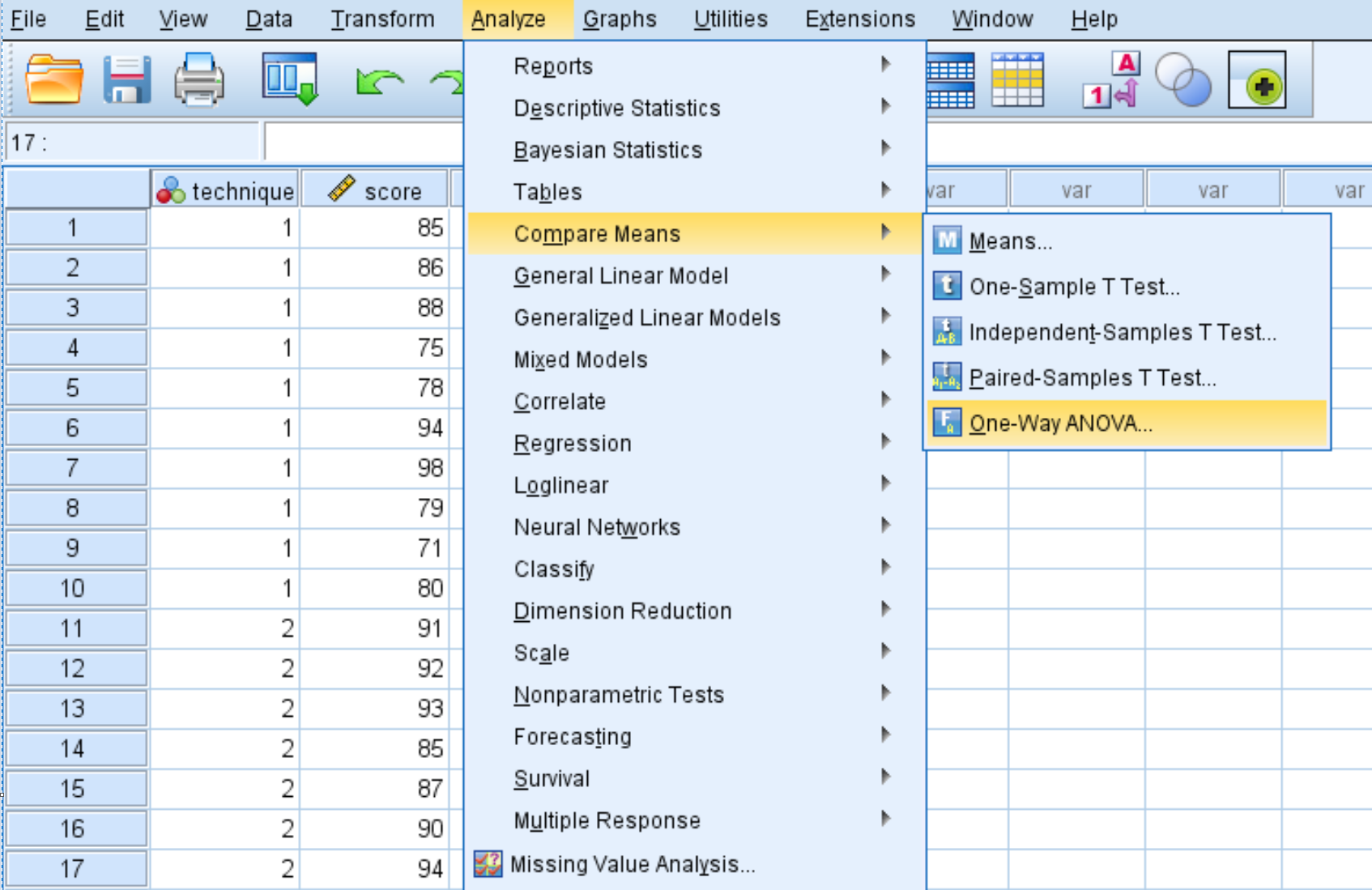
Platzieren Sie im neuen Fenster, das erscheint, den Variablenwert in das Feld mit der Bezeichnung „Abhängige Liste“ und die Variablentechnik in das Feld mit der Bezeichnung „Faktor“.

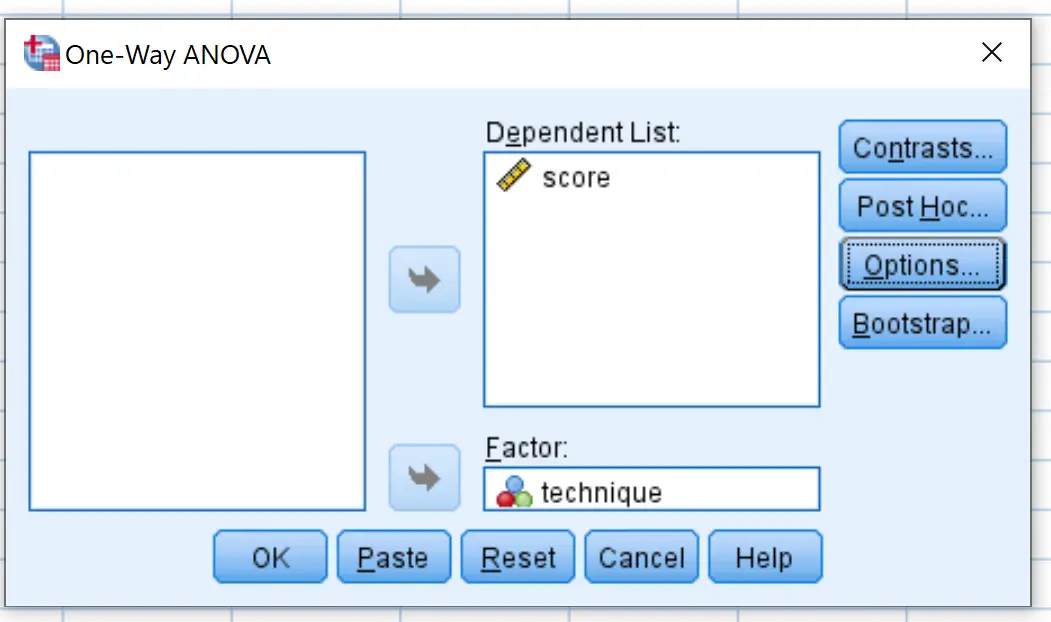
Klicken Sie dann auf Post Hoc und aktivieren Sie das Kontrollkästchen neben Tukey . Klicken Sie dann auf Weiter .

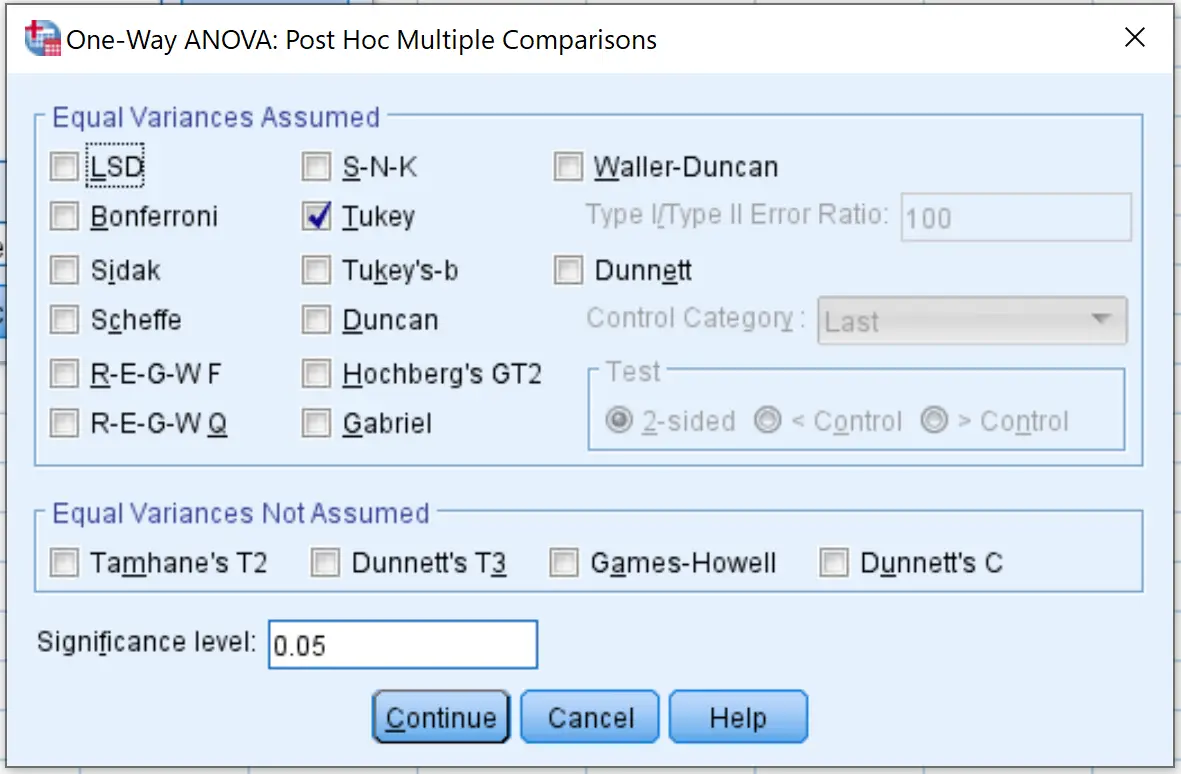
Klicken Sie dann auf Optionen und aktivieren Sie das Kontrollkästchen neben Beschreibend . Klicken Sie dann auf Weiter .

Klicken Sie abschließend auf OK .

Schritt 3: Interpretieren Sie das Ergebnis.

Sobald Sie auf „OK“ klicken, werden die Ergebnisse der einfaktoriellen ANOVA angezeigt. So interpretieren Sie das Ergebnis:

Tabellenbeschreibung

Diese Tabelle zeigt deskriptive Statistiken für jede der drei Gruppen in unserem Datensatz.

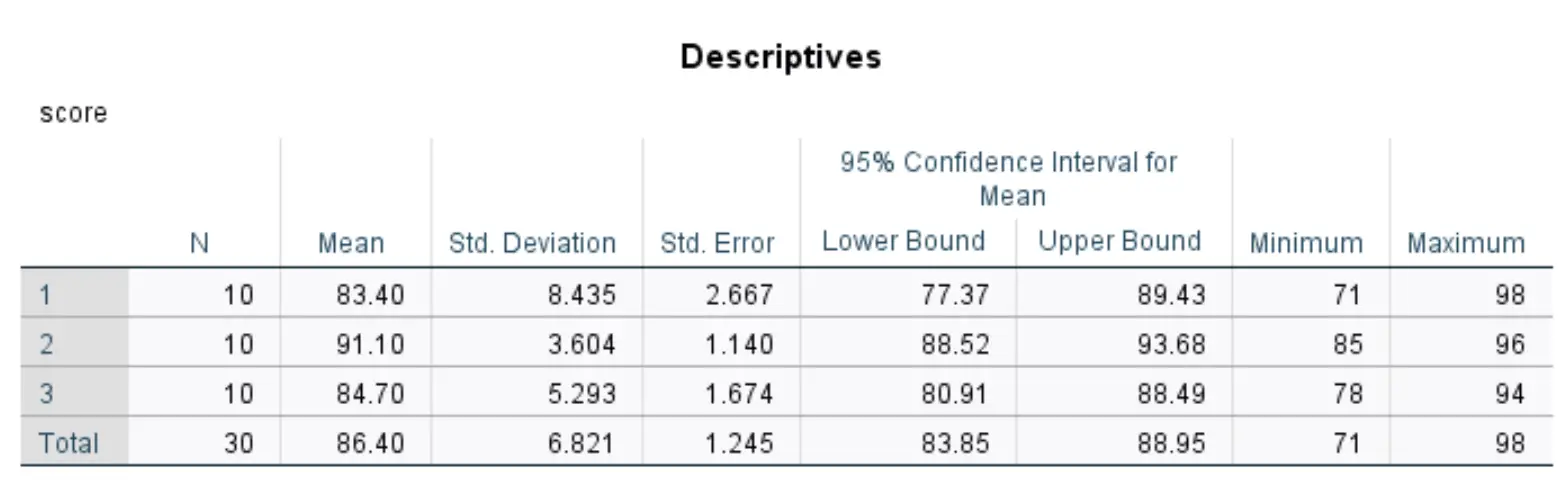
Zu den relevantesten Zahlen zählen:

• N: Die Anzahl der Schüler in jeder Gruppe.
• Durchschnitt: Das durchschnittliche Testergebnis für jede Gruppe.
• Standard. Abweichung: Standardabweichung der Testergebnisse für jede Gruppe.

ANOVA-Tabelle

In dieser Tabelle werden die Ergebnisse der einfaktoriellen ANOVA angezeigt:

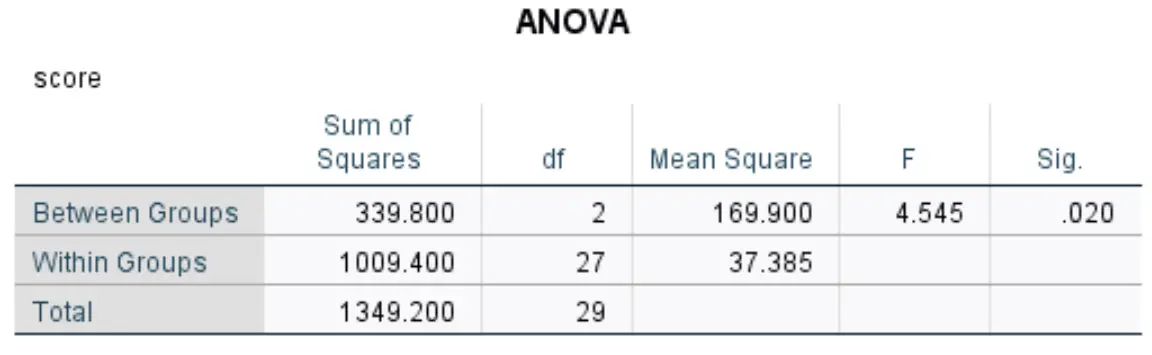
Zu den relevantesten Zahlen zählen:

• F: Die Gesamt-F-Statistik.
• Sig: Der p-Wert, der der F-Statistik (4,545) mit dem Zähler df (2) und dem Nenner df (27) entspricht. In diesem Fall ergibt sich ein p-Wert von 0,020 .

Denken Sie daran, dass eine einfaktorielle ANOVA die folgenden Null- und Alternativhypothesen verwendet:

• H ₀ (Nullhypothese): μ ₁ = μ ₂ = μ ₃ = … = μ _k (alle Populationsmittelwerte sind gleich)
• H _A (Alternativhypothese): Mindestens ein Populationsmittelwert ist unterschiedlich   ausruhen

Da der p-Wert der ANOVA-Tabelle kleiner als 0,05 ist, verfügen wir über ausreichende Beweise, um die Nullhypothese abzulehnen und zu dem Schluss zu kommen, dass sich mindestens einer der Gruppenmittelwerte von den anderen unterscheidet.

Um genau zu wissen, welche Gruppenmittelwerte sich voneinander unterscheiden, können wir auf die letzte Tabelle des ANOVA-Ergebnisses zurückgreifen.

Mehrfachvergleichstabelle

Diese Tabelle zeigt Tukeys Post-hoc-Mehrfachvergleiche zwischen jeder der drei Gruppen. Uns interessiert vor allem Sig. Spalte, die die p-Werte für die Mittelwertunterschiede zwischen den einzelnen Gruppen anzeigt:

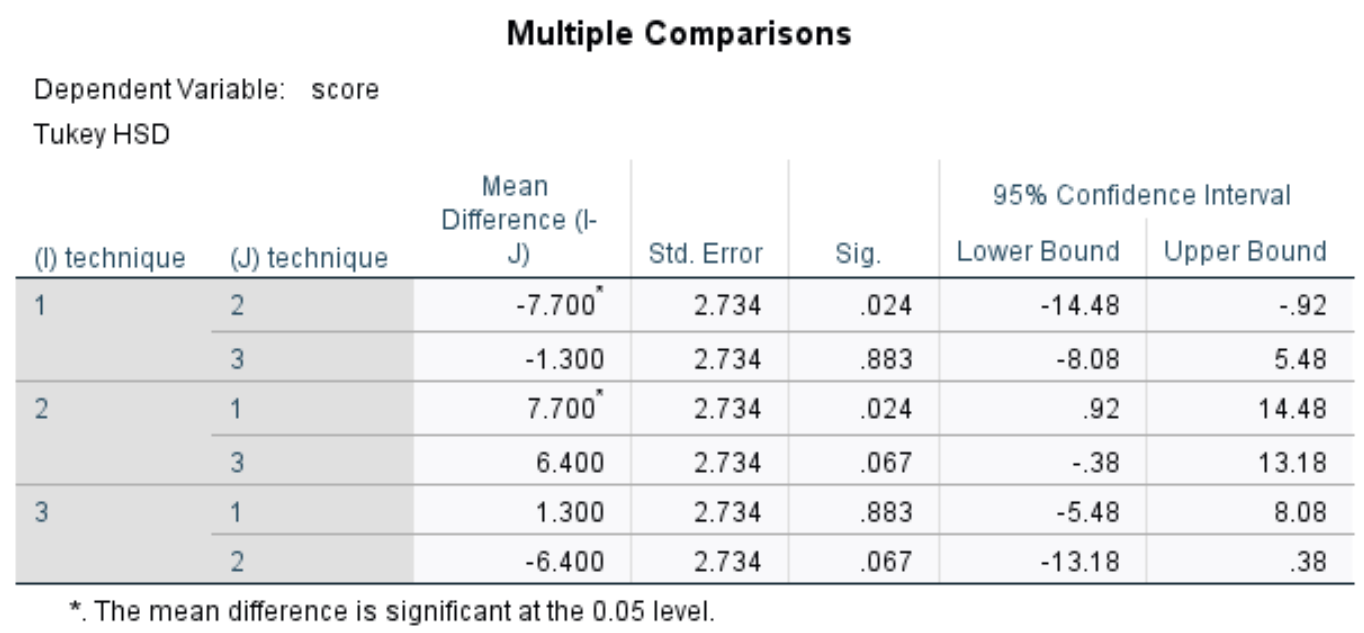
In der Tabelle sehen wir die p-Werte für die folgenden Vergleiche:

• Technik 1 gegen 2: | p-Wert = 0,024
• Technik 1 gegen 3 | p-Wert = 0,883
• Technik 2 gegen 3 | p-Wert = 0,067

Der einzige Gruppenvergleich mit einem p-Wert von weniger als 0,05 besteht zwischen Technik 1 und Technik 2.

Dies zeigt uns, dass es einen statistisch signifikanten Unterschied in den durchschnittlichen Testergebnissen zwischen Schülern gibt, die Technik 1 verwendet haben, und denen, die Technik 2 verwendet haben.

Es gibt jedoch keinen statistisch signifikanten Unterschied zwischen den Techniken 1 und 3 und auch nicht zwischen den Techniken 2 und 3.

Schritt 4: Melden Sie die Ergebnisse.

Schließlich können wir die Ergebnisse der einfaktoriellen ANOVA berichten. Hier ist ein Beispiel dafür:

Eine einfaktorielle ANOVA wurde durchgeführt, um festzustellen, ob drei verschiedene Untersuchungstechniken zu unterschiedlichen Testergebnissen führten.

Insgesamt 10 Studenten nutzten jede der drei Lerntechniken einen Monat lang, bevor sie alle denselben Test ablegten.

Eine einfaktorielle ANOVA ergab, dass es einen statistisch signifikanten Unterschied in den Testergebnissen zwischen mindestens zwei Gruppen gab (F(2, 27) = 4,545, p = 0,020).

Tukeys Test für mehrere Vergleiche ergab, dass die mittleren Testergebnisse zwischen Schülern, die Technik 1 und Technik 2 verwendeten, signifikant unterschiedlich waren (p = 0,024, 95 %-KI = [-14,48, -0,92]).

Es gab keinen statistisch signifikanten Unterschied zwischen den Werten für Techniken 1 und 3 (p = 0,883) oder zwischen den Werten für Techniken 2 und 3 (p = 0,067).