So führen sie eine einfaktorielle anova in stata durch

Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht.

Diese Art von Test wird als einfaktorielle ANOVA bezeichnet, da wir den Einfluss einer Prädiktorvariablen auf eine Antwortvariable analysieren. Wären wir stattdessen an der Auswirkung zweier Prädiktorvariablen auf eine Antwortvariable interessiert, könnten wir eine zweifaktorielle ANOVA durchführen.

In diesem Tutorial wird erklärt, wie eine einfaktorielle ANOVA in Stata durchgeführt wird.

Beispiel: Einfaktorielle ANOVA in Stata

In diesem Beispiel verwenden wir den integrierten Stata-Datensatz namens systolic , um eine einfaktorielle ANOVA durchzuführen. Dieser Datensatz enthält die folgenden drei Variablen für 58 verschiedene Personen:

• Medikament verwendet
• Krankheit des Patienten
• Veränderung des systolischen Blutdrucks

Wir werden die folgenden Schritte verwenden, um eine einfache ANOVA durchzuführen, um festzustellen, ob die Art der verwendeten Medikamente einen signifikanten Einfluss auf die Veränderung des systolischen Blutdrucks hat.

Schritt 1: Daten laden.

Laden Sie zunächst die Daten, indem Sie webuse systolic in das Befehlsfeld eingeben und auf die Eingabetaste klicken.

Schritt 2: Sehen Sie sich die Rohdaten an.

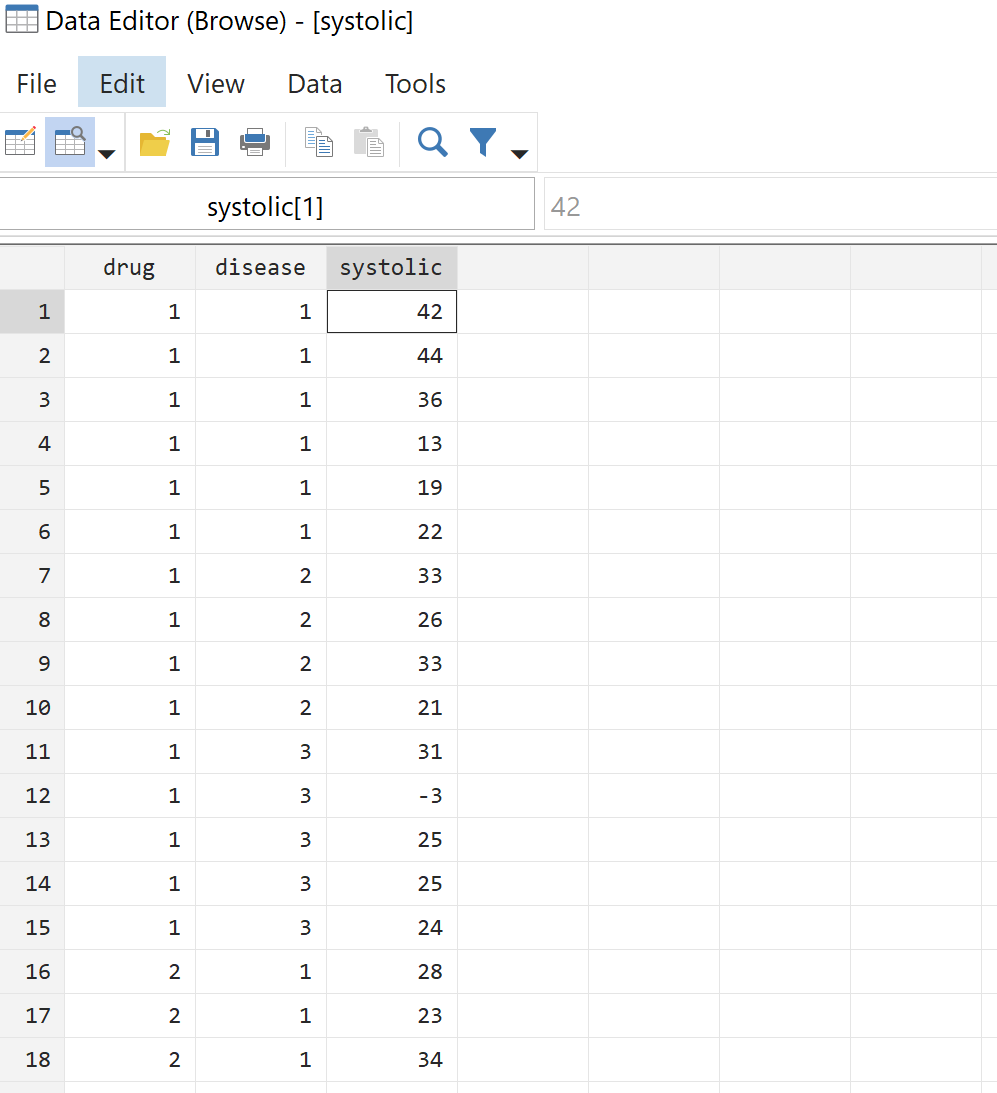
Bevor wir eine einfaktorielle ANOVA durchführen, schauen wir uns zunächst die Rohdaten an. Navigieren Sie in der oberen Menüleiste zu Daten > Dateneditor > Dateneditor (Durchsuchen) . Dies zeigt uns die tatsächlichen Daten für alle 58 Patienten:

Schritt 3: Visualisieren Sie die Daten.

Als nächstes visualisieren wir die Daten. Wir werden Boxplots erstellen, um die Verteilung der systolischen Blutdruckwerte für jede Medikamentenkategorie darzustellen.

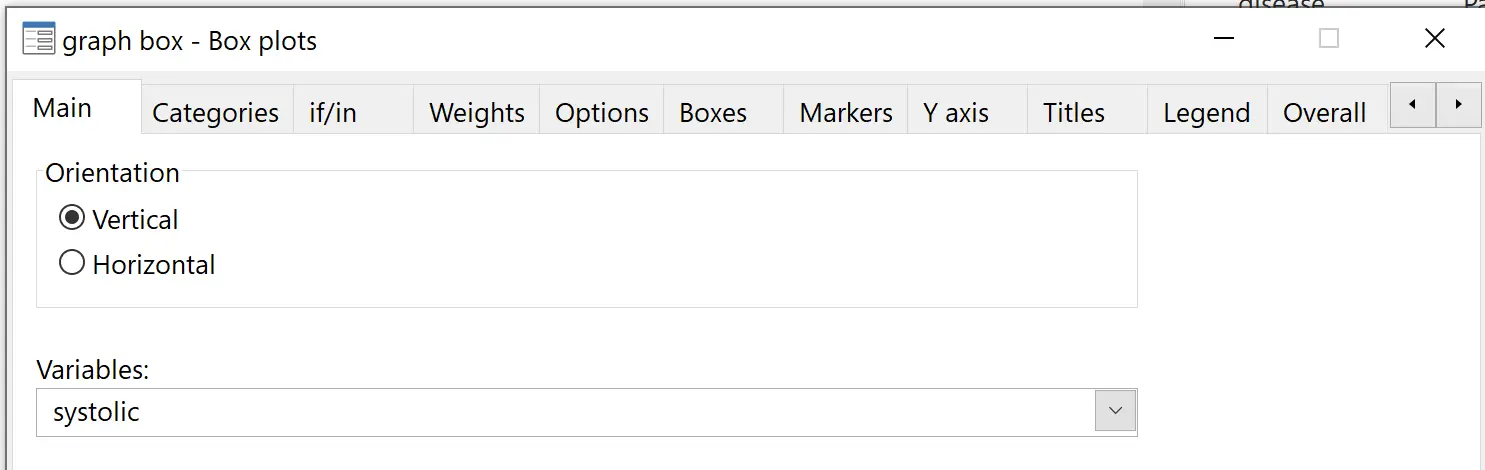
Gehen Sie in der oberen Menüleiste zu Diagramme > Boxplot . Wählen Sie unter Variablen die Option „Systolisch“ aus:

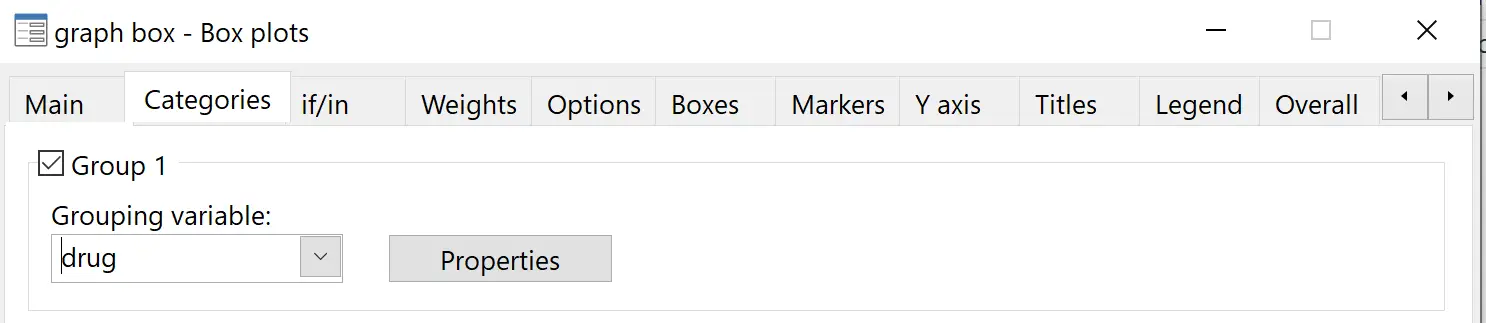
Wählen Sie dann in der Unterüberschrift „Kategorien“ unter „Gruppierungsvariable“ die Option „Medikament“ aus:

Klicken Sie auf OK . Es wird automatisch ein Diagramm mit vier Boxplots angezeigt:

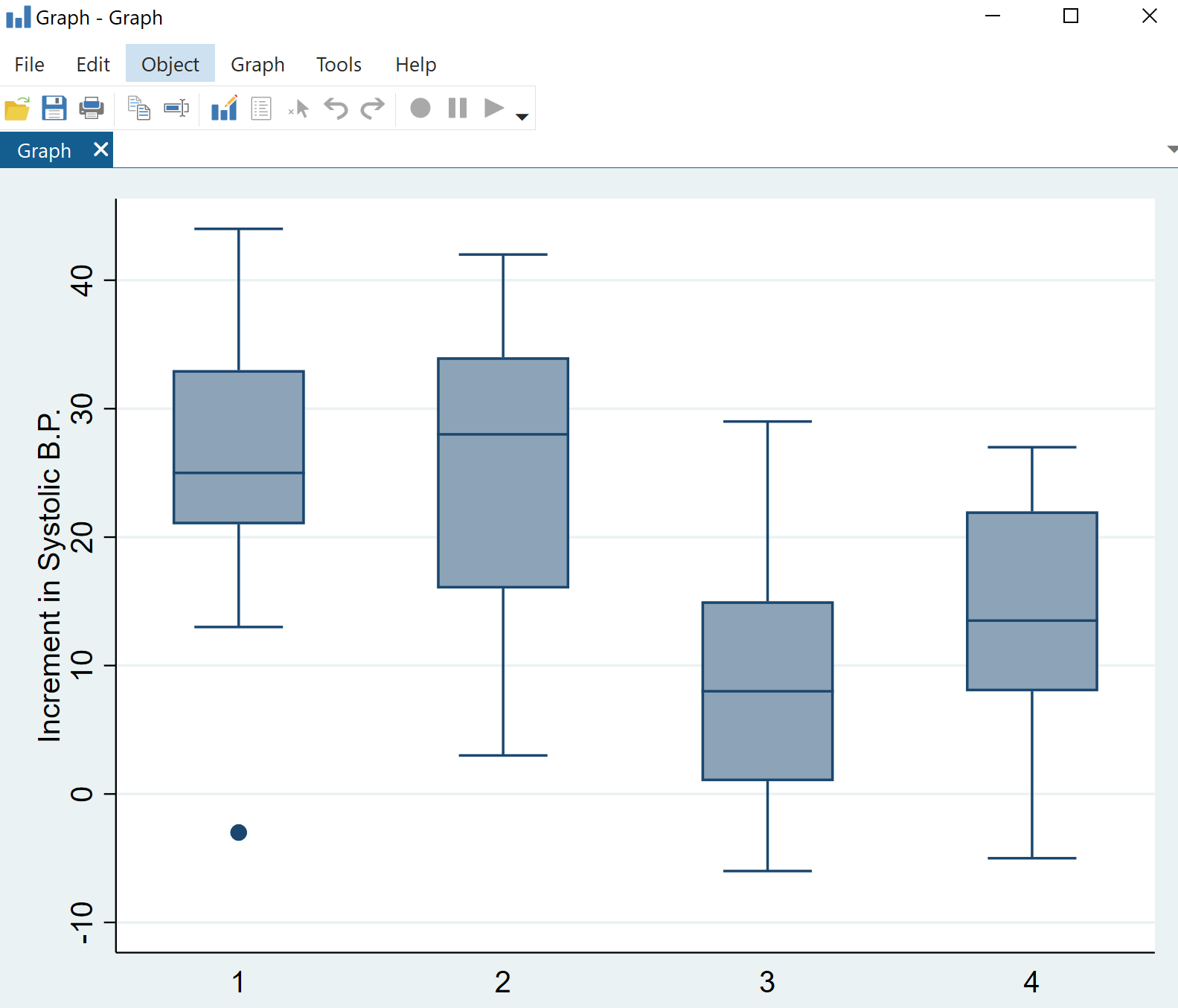
Wir können sofort erkennen, dass die Verteilung der Veränderungen des systolischen Blutdrucks je nach Medikamentenkategorie variiert, aber eine einfaktorielle ANOVA zeigt uns, ob diese Unterschiede statistisch signifikant sind.

Schritt 4: Führen Sie eine einfaktorielle ANOVA durch.

Navigieren Sie in der oberen Menüleiste zu Statistik > Lineare und verwandte Modelle > ANOVA/MANOVA > Einfaktorielle ANOVA .

Wählen Sie unter „Antwortvariable“ die Option „Systolisch“. Wählen Sie unter Faktorvariable das Medikament aus. Klicken Sie dann auf das Kästchen neben „Zusammenfassungstabelle erstellen“ , damit wir einige grundlegende beschreibende Statistiken für jede Gruppe sehen können. Klicken Sie dann auf OK .

Die folgende Ausgabe wird angezeigt:

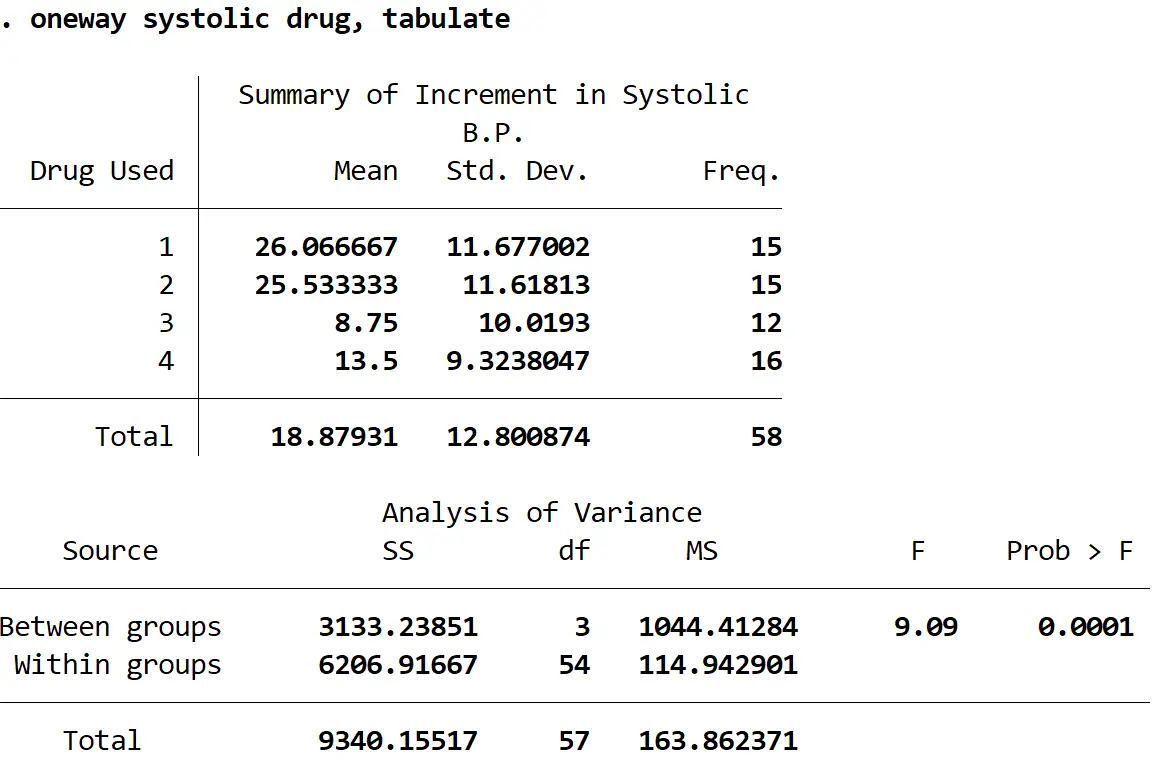
Die F-Statistik beträgt 9,09 und der entsprechende p-Wert beträgt 0,0001 . Da der p-Wert kleiner als Alpha = 0,05 ist, können wir die Nullhypothese zurückweisen, dass die mittlere Änderung des systolischen Blutdrucks für jede Gruppe gleich ist.

Mit anderen Worten: Es gibt einen statistisch signifikanten Unterschied in der mittleren Veränderung des systolischen Blutdrucks zwischen mindestens zwei Medikamentengruppen.

Schritt 5: Führen Sie mehrere Vergleichstests durch.

Dann können wir mehrere Vergleichstests durchführen, um tatsächlich herauszufinden, welche Gruppenmittelwerte sich voneinander unterscheiden.

Navigieren Sie in der oberen Menüleiste zu Statistiken > Zusammenfassungen, Tabellen und Tests > Zusammenfassung und deskriptive Statistik > Paarweise Mittelwertvergleiche .

Wählen Sie für „Variable“ die Variable „Systolische Reaktion“ aus. Wählen Sie für „Over“ die erklärende Variable „ drug“ aus. Wählen Sie für Anpassung für mehrere Vergleiche die Tukey-Methode aus.

Klicken Sie dann unter der Unterüberschrift „Berichte“ auf die Schaltfläche neben „Tabellen der Effekte“ und aktivieren Sie das Kontrollkästchen neben „Tabelle der Effekte mit Konfidenzintervallen und p-Werten anzeigen“ . Klicken Sie dann auf OK .

Folgende Ergebnisse werden angezeigt:

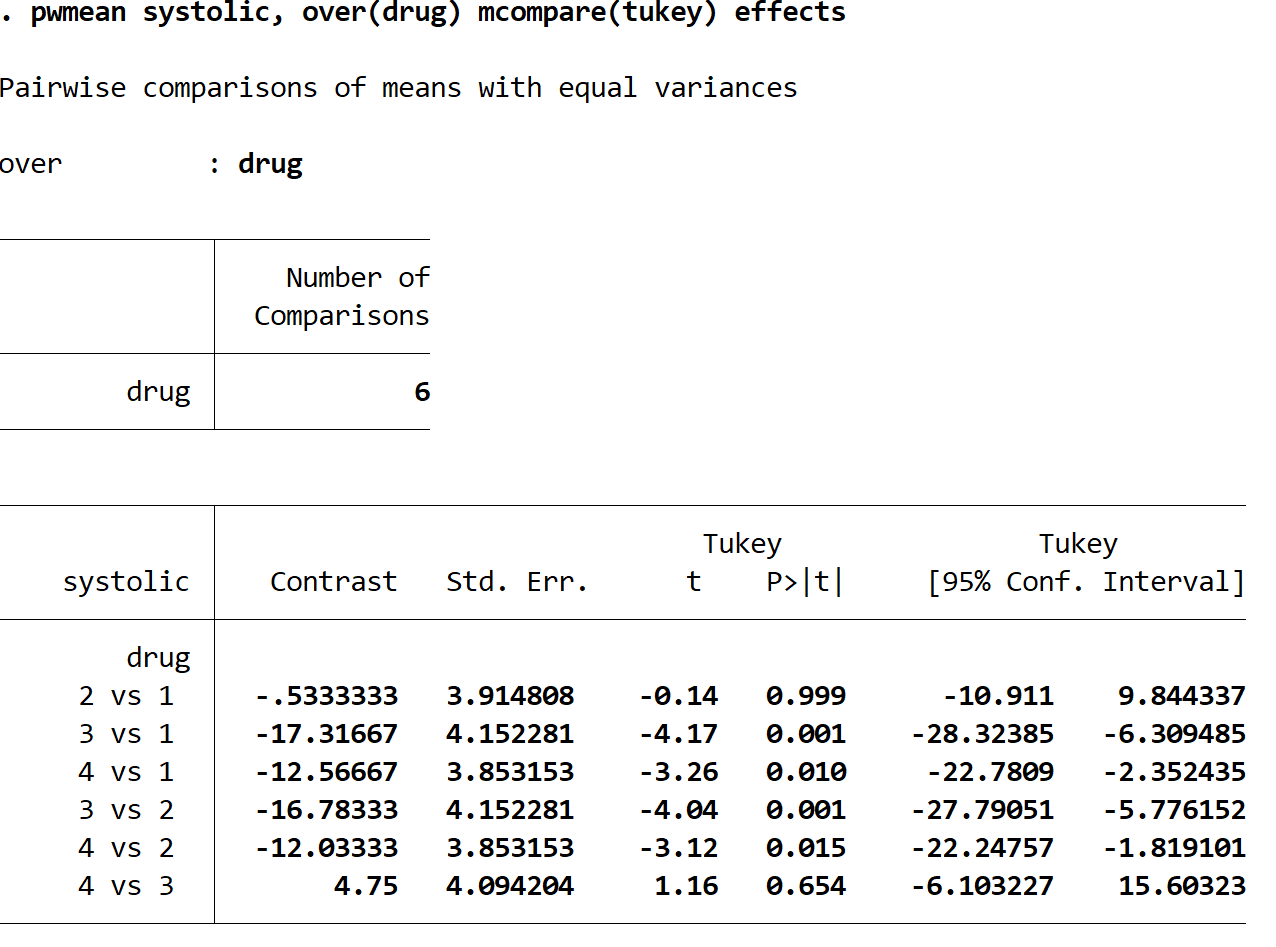
Jede Zeile stellt einen Vergleich zwischen zwei spezifischen Arzneimittelgruppen dar. In der ersten Zeile wird beispielsweise die durchschnittliche Änderung des systolischen Blutdrucks zwischen Medikamentengruppe 2 und Medikamentengruppe 1 verglichen. Der p-Wert für diesen Vergleich beträgt 0,999 , was extrem hoch ist und nicht weniger als 0,05 beträgt. Dies bedeutet, dass es keinen statistisch signifikanten Unterschied zwischen den Arzneimittelgruppen 1 und 2 gibt.

Wir können jedoch sehen, dass die p-Werte für die folgenden Vergleiche alle kleiner als 0,05 sind:

• Medizin 3 zu 1 | p-Wert = 0,001
• Medizin 4 zu 1 | p-Wert = 0,010
• Medizin 3 gegen 2 | p-Wert = 0,001
• Medizin 4 gegen 2 | p-Wert = 0,015

Dies bedeutet, dass der Unterschied in der mittleren Änderung des systolischen Blutdrucks zwischen jeder dieser Gruppen statistisch signifikant ist.

Schritt 6: Melden Sie die Ergebnisse.

Abschließend werden wir über die Ergebnisse unserer einfaktoriellen ANOVA-Analyse berichten. Hier ist ein Beispiel dafür:

Eine einfaktorielle ANOVA wurde durchgeführt, um zu bestimmen, ob vier verschiedene Arten von Medikamenten unterschiedliche Auswirkungen auf den systolischen Blutdruck hatten.

Die folgende Tabelle fasst die Anzahl der Teilnehmer in jeder Gruppe sowie die mittlere Änderung des systolischen Blutdrucks und die Standardabweichung des systolischen Blutdrucks für jede Gruppe zusammen:

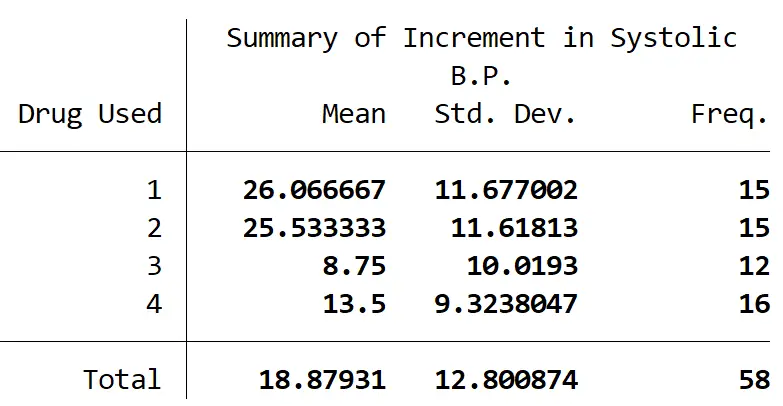
Eine einfaktorielle ANOVA ergab, dass es einen statistisch signifikanten Unterschied zwischen mindestens zwei Gruppen gab (F(3, 54) = 9,09, p = 0,001).

Tukeys Test für mehrere Vergleiche ergab, dass die Veränderung des systolischen Blutdrucks für Medikament 3 statistisch signifikant höher war als für Medikament 1 (17,32 +/- 4,15, p = 0,001), für Medikament 3 im Vergleich zu Medikament 2 (16,78 +/- 4,15, p = 0,001), für Medikament 4 im Vergleich zu Medikament 1 (12,57 +/- 3,85, p = 0,010) und für Medikament 4 im Vergleich zu Medikament 2 (12,03 +/- 3,85, p = 0,015).

Es gab keinen statistisch signifikanten Unterschied zwischen den Medikamentengruppen 1 und 2 (0,533 +/- 3,91, p = 0,999) oder zwischen den Medikamentengruppen 3 und 4 (4,75 +/- 4,09, p = 0,654).