So verwenden sie die elbow-methode in r, um optimale cluster zu finden

Einer der am häufigsten verwendeten Clustering-Algorithmen beim maschinellen Lernen ist das sogenannte K-Means-Clustering .

K-Means-Clustering ist eine Technik, bei der wir jede Beobachtung aus einem Datensatz in einem von K Clustern platzieren.

Das Endziel besteht darin, K- Cluster zu haben, in denen die Beobachtungen innerhalb jedes Clusters einander ziemlich ähnlich sind, während sich die Beobachtungen in verschiedenen Clustern deutlich voneinander unterscheiden.

Beim K-Means-Clustering besteht der erste Schritt darin, einen Wert für K auszuwählen – die Anzahl der Cluster, in denen wir Beobachtungen platzieren möchten.

Eine der gebräuchlichsten Methoden zur Auswahl eines Werts für K ist die sogenannte Ellbogenmethode . Dabei wird ein Diagramm mit der Anzahl der Cluster auf der x-Achse und der Summe der Quadratsummen auf der y-Achse erstellt und anschließend identifiziert wo ein „Knie“ oder eine Wendung in der Handlung erscheint.

Der Punkt auf der x-Achse, an dem das „Knie“ auftritt, gibt uns die optimale Anzahl von Clustern an, die im k-means-Clustering-Algorithmus verwendet werden sollen.

Das folgende Beispiel zeigt, wie die Ellbogenmethode in R verwendet wird.

Beispiel: Verwendung der Ellbogenmethode in R

Für dieses Beispiel verwenden wir den in R integrierten Datensatz „USArrests “, der die Anzahl der Festnahmen pro 100.000 Einwohner in jedem US-Bundesstaat im Jahr 1973 wegen Mordes, Körperverletzung und Vergewaltigung sowie den Prozentsatz der Stadtbevölkerung jedes Bundesstaates enthält Bereiche. , UrbanPop.

Der folgende Code zeigt, wie Sie den Datensatz laden, Zeilen mit fehlenden Werten entfernen und jede Variable im Datensatz skalieren, um einen Mittelwert von 0 und eine Standardabweichung von 1 zu erhalten:

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Um die optimale Anzahl von Clustern für den k-means-Algorithmus zu finden, verwenden wir die Funktion fviz_nbclust() aus dem Paket factoextra , um ein Diagramm der Anzahl der Cluster im Vergleich zur Gesamtsumme der Quadrate zu erstellen:

 library (cluster)
library (factoextra)

#create plot of number of clusters vs total within sum of squares
fviz_nbclust(df, kmeans, method = “ wss ”) 

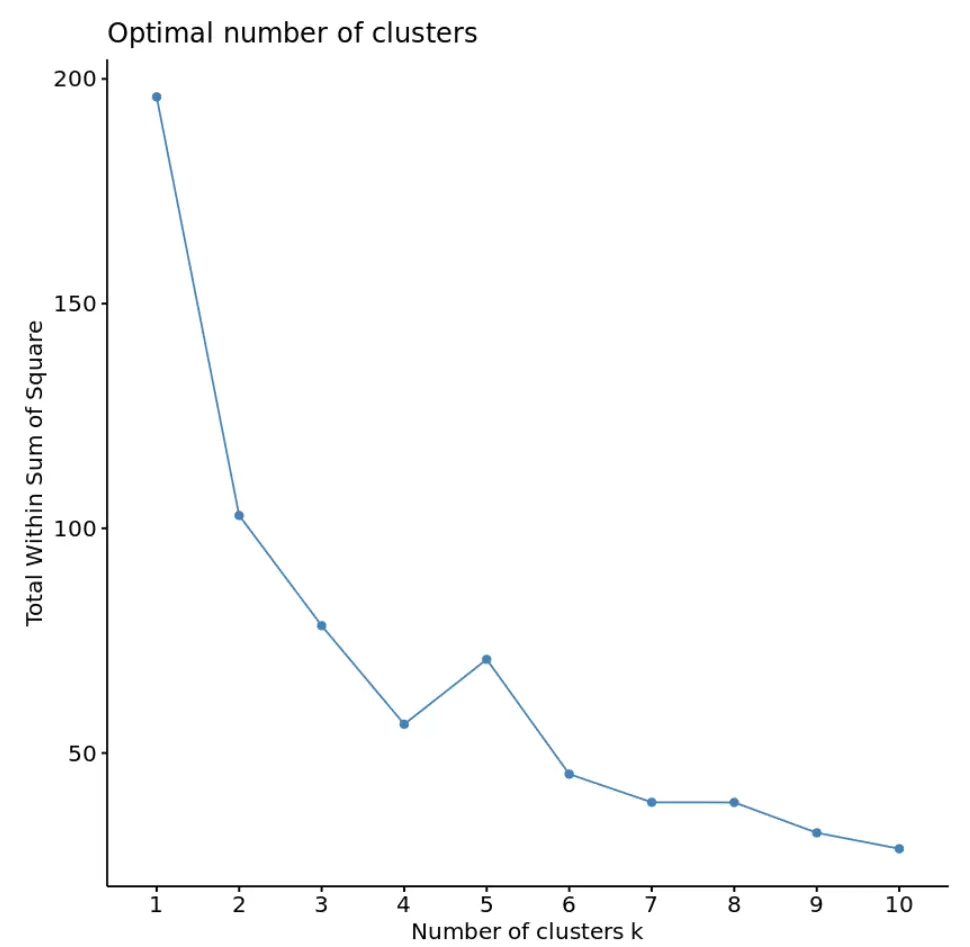
In diesem Diagramm scheint es, dass es bei k = 4 Clustern ein „Knie“ oder einen Knick gibt. Dies ist der Punkt, an dem sich die Gesamtsumme der Quadrate zu stabilisieren beginnt.

Dies sagt uns, dass die optimale Anzahl von Clustern für die Verwendung im K-Means-Algorithmus 4 beträgt.

Hinweis : Obwohl wir durch die Verwendung von mehr Clustern möglicherweise eine niedrigere Summe der Quadrate erhalten, würden wir die Trainingsdaten wahrscheinlich überanpassen und daher würde der k-means-Algorithmus bei den Testdaten nicht so gut funktionieren.

Wir können die Funktion kmeans() aus dem Cluster- Paket verwenden, um k-means-Clustering für den Datensatz unter Verwendung des optimalen Werts für k von 4 durchzuführen:

 #make this example reproducible
set. seeds (1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

Anhand der Ergebnisse können wir Folgendes erkennen:

• Dem ersten Cluster wurden 16 Staaten zugeordnet
• Dem zweiten Cluster sind 13 Staaten zugeordnet
• Dem dritten Cluster wurden 13 Staaten zugeordnet
• Dem vierten Cluster wurden 8 Staaten zugeordnet

Wir können auch die Clusterzuordnungen jedes Staates zum Originaldatensatz hinzufügen:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Jede Beobachtung aus der Originaldatenbank wurde einer von vier Gruppen zugeordnet.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten Schritt-für-Schritt-Beispiele zur Ausführung verschiedener Clustering-Algorithmen in R:

K-Means-Clustering in R: Schritt-für-Schritt-Beispiel
K-Medoids-Clustering in R: Schritt-für-Schritt-Beispiel
Hierarchisches Clustering in R: Schritt-für-Schritt-Beispiel