So ermitteln sie eine wahrscheinlichkeit anhand eines mittelwerts und einer standardabweichung

Wir können den folgenden Prozess verwenden, um die Wahrscheinlichkeit einer normalverteilten Zufallsvariablen zu ermitteln

Schritt 1: Finden Sie den Z-Score.

Ein Z-Score gibt an, um wie viele Standardabweichungen ein einzelner Datenwert vom Mittelwert abweicht. Es wird wie folgt berechnet:

Z-Score = (x – μ) / σ

Gold:

• x: individueller Datenwert
• μ: Bevölkerungsdurchschnitt
• σ: Populationsstandardabweichung

Schritt 2: Finden Sie die Wahrscheinlichkeit, die dem Z-Score entspricht.

Sobald wir den Z-Score berechnet haben, können wir die entsprechende Wahrscheinlichkeit in der Z-Tabelle finden.

Die folgenden Beispiele zeigen, wie dieser Prozess in verschiedenen Szenarien verwendet wird.

Beispiel 1: Wahrscheinlichkeit kleiner als ein bestimmter Wert

Die Ergebnisse bei einem bestimmten Test sind normalverteilt mit dem Mittelwert μ = 82 und der Standardabweichung σ = 8. Wie groß ist die Wahrscheinlichkeit, dass ein bestimmter Schüler beim Test weniger als 84 Punkte erzielt?

Schritt 1: Finden Sie den Z-Score.

Zuerst finden wir den Z-Score, der einem Score von 84 zugeordnet ist:

z-Score = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Schritt 2: Verwenden Sie die Z-Tabelle, um die entsprechende Wahrscheinlichkeit zu ermitteln.

Als nächstes suchen wir in der Z-Tabelle nach dem Wert 0,25 :

Die Wahrscheinlichkeit, dass ein bestimmter Schüler weniger als 84 Punkte erzielt, beträgt etwa 59,87 % .

Beispiel 2: Wahrscheinlichkeit größer als ein bestimmter Wert

Die Körpergröße einer bestimmten Pinguinart ist normalverteilt mit einem Mittelwert von μ = 30 Zoll und einer Standardabweichung von σ = 4 Zoll. Wenn wir einen Pinguin zufällig auswählen, wie hoch ist die Wahrscheinlichkeit, dass er größer als 28 Zoll ist?

Schritt 1: Finden Sie den Z-Score.

Zuerst ermitteln wir den Z-Score, der einer Körpergröße von 28 Zoll zugeordnet ist.

Punktzahl z = (x – μ) / σ = (28 – 30) / 4 = -2 / 4 = -0,5

Schritt 2: Verwenden Sie die Z-Tabelle, um die entsprechende Wahrscheinlichkeit zu ermitteln.

Als nächstes suchen wir nach dem Wert -0,5   in Tabelle z:

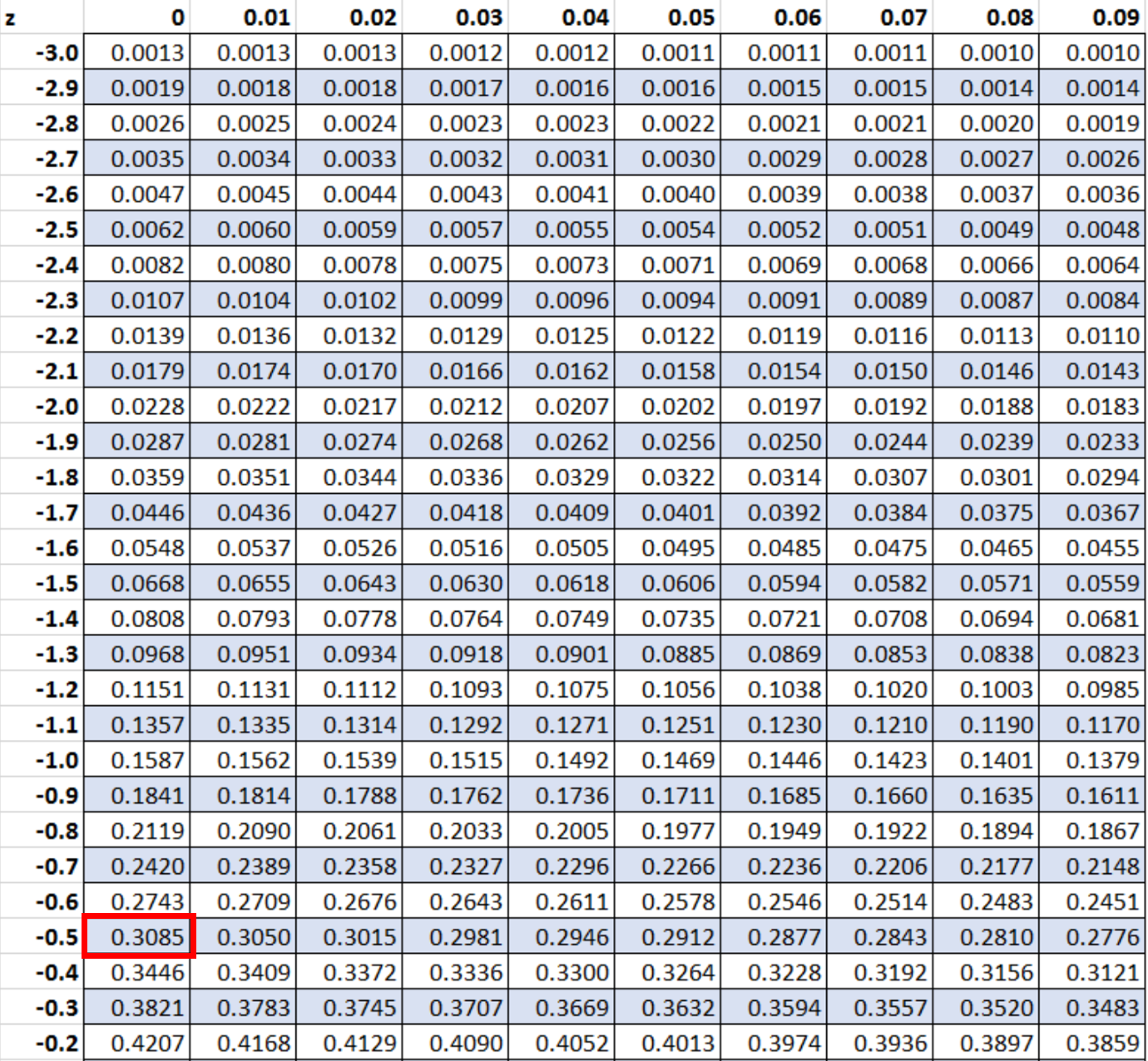
Der Wert, der einem Z-Score von -0,5 entspricht, ist 0,3085. Dies stellt die Wahrscheinlichkeit dar, dass ein Pinguin kleiner als 28 Zoll ist.

Da wir jedoch die Wahrscheinlichkeit wissen möchten, dass ein Pinguin größer als 28 Zoll ist, müssen wir diese Wahrscheinlichkeit von 1 subtrahieren.

Die Wahrscheinlichkeit, dass ein Pinguin größer als 28 Zoll ist, beträgt also: 1 – 0,3085 = 0,6915 .

Beispiel 3: Wahrscheinlichkeit zwischen zwei Werten

Das Gewicht einer bestimmten Schildkrötenart ist normalverteilt mit einem Mittelwert von μ = 400 Pfund und einer Standardabweichung von σ = 25 Pfund. Wenn wir eine Schildkröte zufällig auswählen, wie hoch ist die Wahrscheinlichkeit, dass sie zwischen 410 und 425 Pfund wiegt?

Schritt 1: Finden Sie die Z-Scores.

Zunächst ermitteln wir die Z-Scores für 410 Bücher und 425 Bücher

Z-Score von 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

z-Score von 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Schritt 2: Verwenden Sie die Z-Tabelle, um die entsprechende Wahrscheinlichkeit zu ermitteln.

Zuerst suchen wir nach dem Wert 0,4   in Tabelle z:

Als nächstes suchen wir nach dem Wert 1   in Tabelle z:

Als nächstes subtrahieren wir den kleineren Wert vom größeren Wert: 0,8413 – 0,6554 = 0,1859 .

Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Schildkröte zwischen 410 Pfund und 425 Pfund wiegt, beträgt also 18,59 % .

Zusätzliche Ressourcen

So berechnen Sie manuell einen P-Wert aus einem Z-Score
So konvertieren Sie Z-Scores in Roh-Scores
So finden Sie Z-Werte in einem bestimmten Bereich