5 beispiele für die berechnung des erwartungswerts im wirklichen leben

Der Erwartungswert ist ein Wert, der uns den erwarteten Durchschnitt angibt, den eine Zufallsvariable in einer unendlichen Anzahl von Versuchen annehmen wird.

Wir verwenden die folgende Formel, um den Erwartungswert eines Ereignisses zu berechnen:

Erwarteter Wert = Σx * P(x)

Gold:

• x : Datenwert
• P(x) : Wertwahrscheinlichkeit

Diese Formel mag etwas verwirrend erscheinen, aber sie ergibt mehr Sinn, wenn Sie sie im Kontext realer Beispiele verwenden.

Die folgenden Beispiele zeigen, wie der Erwartungswert in fünf verschiedenen realen Situationen berechnet wird.

Beispiel 1: Investitionen

Der Erwartungswert wird von Handelsunternehmen häufig verwendet, um den erwarteten Gewinn oder Verlust einer Investition zu bestimmen.

Angenommen, eine bestimmte Anlage kann mit einer Wahrscheinlichkeit von 0,95 eine jährliche Rendite von 5 %, mit einer Wahrscheinlichkeit von 0,05 aber auch eine jährliche Rendite von -20 % erzielen.

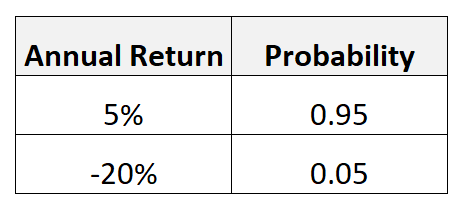
Den erwarteten Wert dieser Investition würden wir wie folgt berechnen:

• Erwarteter Wert = 5 %*,95 + (-20 %)*,05 = 3,75 %

Diese besondere Investition hat einen positiven Erwartungswert.

Das heißt, wenn wir unendlich oft in diese spezielle Anlage investieren würden, würden wir eine langfristige durchschnittliche jährliche Rendite von 3,75 % erwarten.

Beispiel 2: Wetter

Der Erwartungswert wird häufig von Agrarunternehmen verwendet, um die erwartete Regenmenge zu bestimmen, die in einer bestimmten Jahreszeit fallen wird.

Angenommen, es besteht eine Wahrscheinlichkeit von 20 %, dass 1 Zoll Regen fällt, eine Wahrscheinlichkeit von 70 %, dass es 2 Zoll Regen fällt, und eine Wahrscheinlichkeit von 10 %, dass es 3 Zoll Regen gibt.

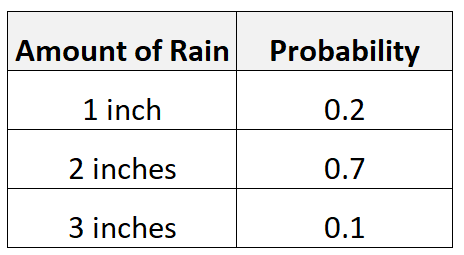
Den Erwartungswert der Regenmenge würden wir wie folgt berechnen:

• Erwarteter Wert = 0,2*1 + 0,7*2 + 0,1*3 = 1,9 Zoll

Beispiel 3: Glücksspiele

Der Erwartungswert wird von Spielern oft verwendet, um zu bestimmen, wie viel sie bei einem bestimmten Spiel potenziell gewinnen könnten.

Angenommen, in einem bestimmten Spiel besteht eine 5 %ige Chance, 100 $ zu gewinnen, eine 50 %ige Chance, 0 $ zu gewinnen, und eine 45 %ige Chance, 20 $ zu verlieren.

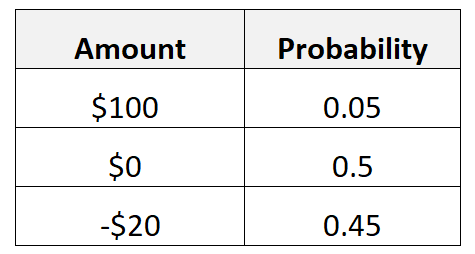
Wir würden den erwarteten Wert der Gewinne wie folgt berechnen:

• Erwarteter Wert = 0,05*100$ + 0,5*0$ + 0,45*(-20$) = -4$

Das heißt, wenn wir dieses Spiel unendlich oft spielen würden, würden wir damit rechnen, jedes Mal, wenn wir spielen, durchschnittlich 4 $ zu verlieren.

Beispiel 4: Geschäft

Der Erwartungswert wird von Unternehmen häufig zur Berechnung der erwarteten Rendite ihrer Werbeausgaben herangezogen.

Nehmen wir beispielsweise an, dass für eine bestimmte Anzeige eine 10-prozentige Chance besteht, eine Rendite von 5 $ zu erhalten, eine 30-prozentige Chance, eine Rendite von 2 $ zu erhalten, und eine 60-prozentige Chance, eine Rendite von -$8 zu erhalten.

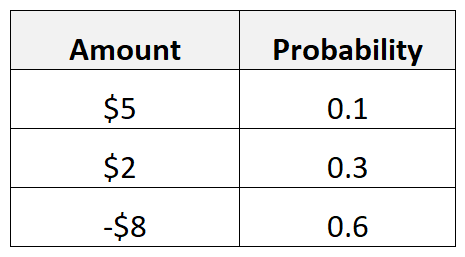
Wir würden den erwarteten Wert der Anzeige wie folgt berechnen:

• Erwarteter Wert = 0,1*5$ + 0,3*2$ + 0,6*(-8$) = -3,70$

Diese spezielle Werbung hat einen negativen Erwartungswert.

Das heißt, wenn das Unternehmen diese bestimmte Anzeige unendlich oft nutzen würde, müsste es jedes Mal durchschnittlich 3,70 US-Dollar verlieren.

Beispiel 5: Unternehmertum

Der erwartete Wert wird oft von Einzelpersonen verwendet, um zu entscheiden, ob sie Unternehmertum betreiben wollen oder nicht.

Angenommen, eine Person glaubt, dass sie, wenn sie ihren Job kündigt und sich selbstständig macht, eine 60-prozentige Chance hat, im ersten Jahr 20.000 US-Dollar zu verdienen, eine 30-prozentige Chance, 60.000 US-Dollar zu verdienen, und eine 10-prozentige Chance, 20.000 US-Dollar zu gewinnen. 0 $.

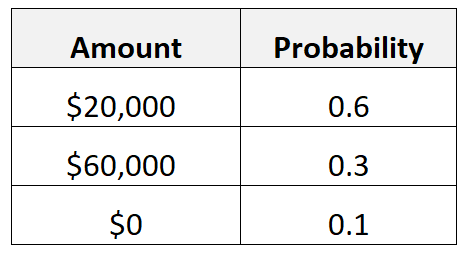
Wir würden den erwarteten Wert ihres Einkommens im ersten Jahr des Unternehmertums wie folgt berechnen:

• Erwarteter Wert = 0,6*20.000 $ + 0,3*60.000 $ + 0,1*0 $ = 30.000 $

Je nachdem, ob dieser Geldbetrag ausreicht oder nicht, kann der Einzelne dann entscheiden, ob er seinen aktuellen Job behalten oder aufgeben möchte.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zum erwarteten Wert:

So berechnen Sie den erwarteten Wert in Excel
So berechnen Sie den erwarteten Wert in R (mit Beispielen)
Erwarteter Wert versus Durchschnitt: Was ist der Unterschied?