So berechnen sie den erwarteten wert von x^2

Für eine Zufallsvariable mit der Bezeichnung X können Sie die folgende Formel verwenden, um den erwarteten Wert von X ² zu berechnen:

E(X ² ) = Σx ² * p(x)

Gold:

• Σ : Ein Symbol, das „Summe“ bedeutet
• x : Der Wert der Zufallsvariablen
• p(x) : Die Wahrscheinlichkeit, dass die Zufallsvariable einen bestimmten Wert annimmt

Das folgende Beispiel zeigt, wie diese Formel in der Praxis angewendet wird.

Beispiel: Berechnung des Erwartungswertes von X ²

Angenommen, wir haben die folgende Wahrscheinlichkeitsverteilungstabelle, die die Wahrscheinlichkeit beschreibt, dass eine Zufallsvariable

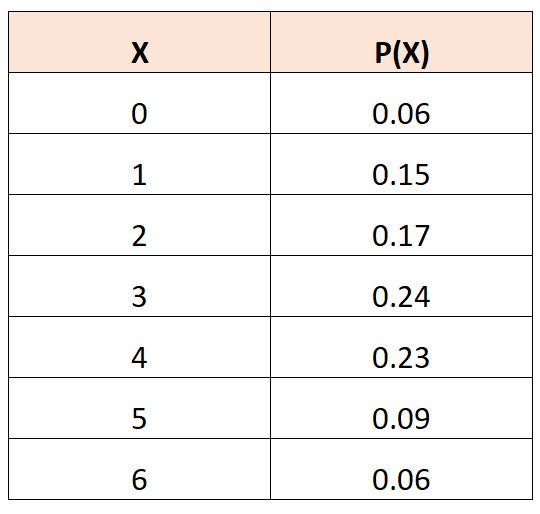
Um den erwarteten Wert von X ² zu berechnen, können wir die folgende Formel verwenden:

E(X ² ) = Σx ² * p(x)

E(X ² ) = (0) ² *.06 + (1) ² *.15 + (2) ² *.17 + (3) ² *.24 + (4) ² *.23 + (5) ² *.09 + (6) ² *.06

E(X ² ) = 0 + 0,15 + 0,68 + 2,16 + 3,68 + 2,25 + 2,16

E( ^X2 ) = 11,08

Der erwartete Wert von X ² beträgt 11,08 .

Beachten Sie, dass es sich bei dieser Zufallsvariablen um eine diskrete Zufallsvariable handelt, das heißt, sie kann nur eine endliche Anzahl von Werten annehmen.

Wenn X eine kontinuierliche Zufallsvariable ist, müssen wir die folgende Formel verwenden, um den erwarteten Wert von X ² zu berechnen:

E(X ² ) = ∫ x ² f(x)dx

Gold:

• ∫: Ein Symbol, das „Integration“ bedeutet
• f(x) : Das PDF wird für die Zufallsvariable fortgesetzt

Bei der Berechnung des erwarteten Werts von ^X2 für eine kontinuierliche Zufallsvariable verwenden wir normalerweise Statistiksoftware, da diese Berechnung manuell schwieriger durchzuführen sein kann.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in der Statistik ausführen:

So ermitteln Sie den Mittelwert einer Wahrscheinlichkeitsverteilung
So ermitteln Sie die Standardabweichung einer Wahrscheinlichkeitsverteilung
So ermitteln Sie die Varianz einer Wahrscheinlichkeitsverteilung