So berechnen sie den erwarteten wert von x^3

Für eine Zufallsvariable mit der Bezeichnung X können Sie die folgende Formel verwenden, um den erwarteten Wert von X ³ zu berechnen:

E(X ³ ) = Σx ³ * p(x)

Gold:

• Σ : Ein Symbol, das „Summe“ bedeutet
• x : Der Wert der Zufallsvariablen
• p(x) : Die Wahrscheinlichkeit, dass die Zufallsvariable einen bestimmten Wert annimmt

Das folgende Beispiel zeigt, wie diese Formel in der Praxis angewendet wird.

Beispiel: Berechnung des Erwartungswertes von X ³

Angenommen, wir haben die folgende Wahrscheinlichkeitsverteilungstabelle, die die Wahrscheinlichkeit beschreibt, dass eine Zufallsvariable

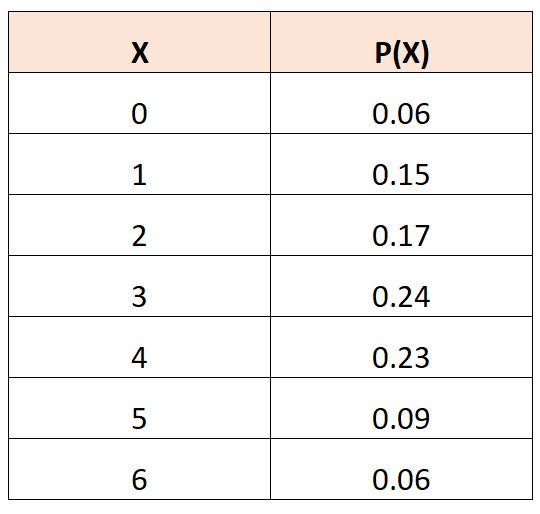
Um den erwarteten Wert von X ³ zu berechnen, können wir die folgende Formel verwenden:

E(X ³ ) = Σx ³ * p(x)

E(X ³ ) = (0) ³ *.06 + (1) ³ *.15 + (2) ³ *.17 + (3) ³ *.24 + (4) ³ *.23 + (5) ³ *.09 + (6) ³ *.06

E(X ³ ) = 0 + 0,15 + 0,1,36 + 6,48 + 14,72 + 11,25 + 12,96

E(X ³ ) = 45,596

Der erwartete Wert von X ³ beträgt 45.596 .

Beachten Sie, dass es sich bei dieser Zufallsvariablen um eine diskrete Zufallsvariable handelt, das heißt, sie kann nur eine endliche Anzahl von Werten annehmen.

Wenn X eine kontinuierliche Zufallsvariable ist, müssen wir die folgende Formel verwenden, um den erwarteten Wert von X ³ zu berechnen:

E(X ³ ) = ∫ x ³ f(x)dx

Gold:

• ∫: Ein Symbol, das „Integration“ bedeutet
• f(x) : Das PDF wird für die Zufallsvariable fortgesetzt

Bei der Berechnung des Erwartungswertes ^von

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in der Statistik ausführen:

So ermitteln Sie den Mittelwert einer Wahrscheinlichkeitsverteilung
So ermitteln Sie die Standardabweichung einer Wahrscheinlichkeitsverteilung
So ermitteln Sie die Varianz einer Wahrscheinlichkeitsverteilung